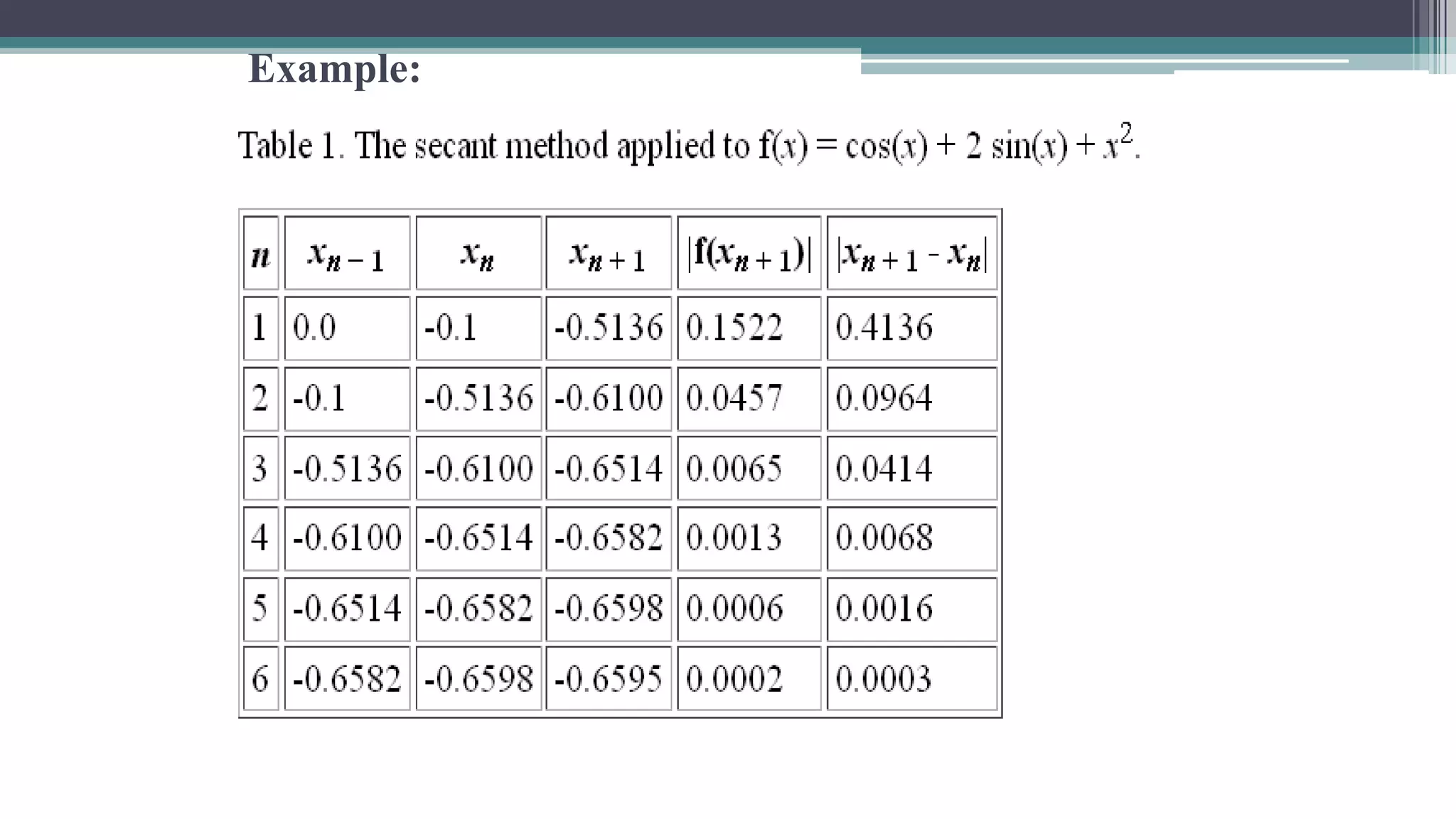
The document discusses numerical methods for finding roots of equations, focusing on three techniques: the Bisection method, Regula-Falsi method, and Secant method. Each method is detailed with algorithms, step-by-step procedures, and examples. The document emphasizes the importance of initial guesses and accuracy in the root-finding process.

1. Numerical and Statistical Methods
Vadodara Institute of Engineering
Kotambi, waghodia
Created by:
Ruchi Maurya

2. Roots of equation by Numerical methods:
• Bisection method
• Regula-Falsi method
• Secant method

3. Bisection method:
• Based on the fact that the function will change signs as it passes
thru the root.
 f(a)*f(b) < 0
• Once we have a root bracketed, we simply evaluate the mid-
point and halve the interval.
• C=(a+b)/2

4. Bisection method:
a bc
f(a)>0
f(b)<0
f(c)>0
c ba
a = c
f(a)>0
f(b)<0
f(c)<0

5. Bisection method:
• C=(a+b)/2
b
ca
b = c
f(b)<0

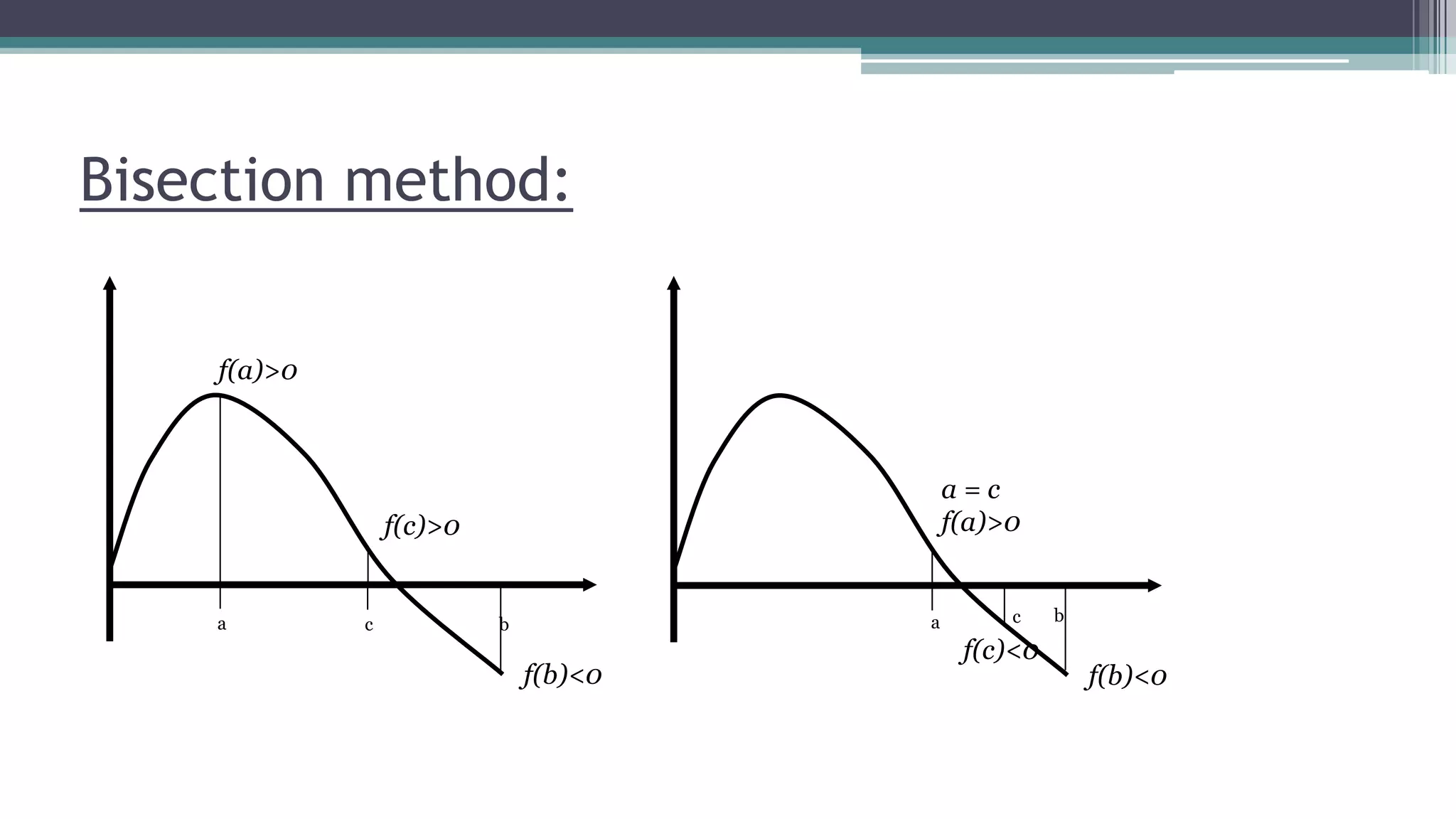
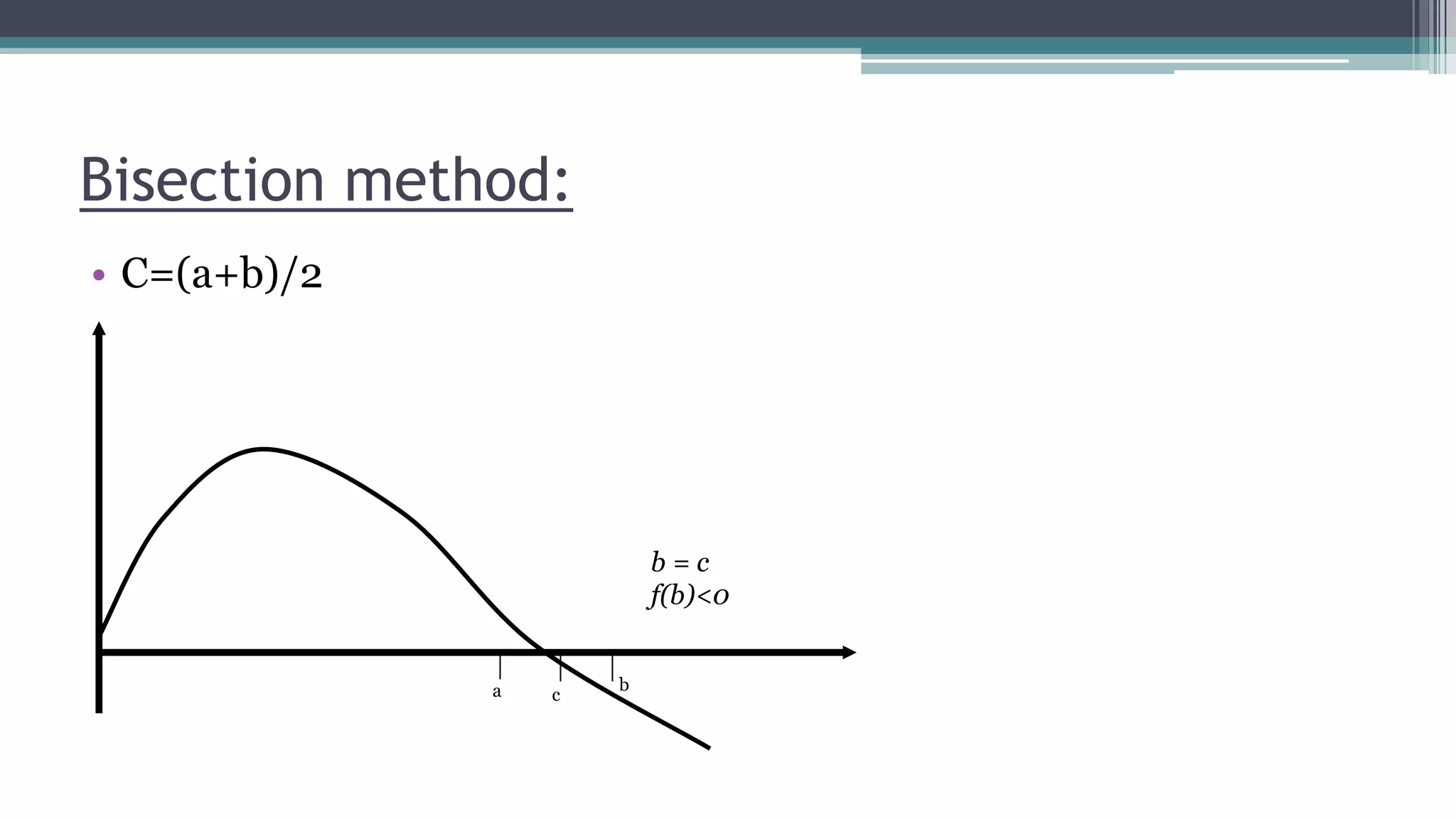
6. Algorithm:
1) Start
2) Read values of x0, x1 and e
*Here x0 and x1 are the two initial guesses
e is the degree of accuracy or the absolute error i.e. the
stopping criteria*
3) Computer function values f(x0) and f(x1)
4) Check whether the product of f(x0) and f(x1) is negative
or
not.
If it is positive take another initial guesses.
If it is negative then goto step 5.
5) Determine:
x = [x0+ x1] / 2

7. 6) Check whether the product of f(x1) and f(x) is
negative or not.
If it is negative, then assign x0 = x;
If it is positive, assign x1 = x;
7) Check whether the value of f(x) is greater than
0.00001 or not.
If yes, goto step 5.
If no, goto step 8.
*Here the value 0.00001 is the desired degree of
accuracy, and hence the stopping criteria.
8) Display the root as x.
9) Stop

8. Example:

9. • Based on the fact that the function will change signs as it passes
thru the root.
 f(a)*f(b) < 0
• Same as Bisection method, only the equation of finding value of ‘c’
is different.
Regula-Falsi method:
)()(
)(.)(.
C
afbf
afbbfa




10. Regula-Falsi method:
a
bcc1
a
b

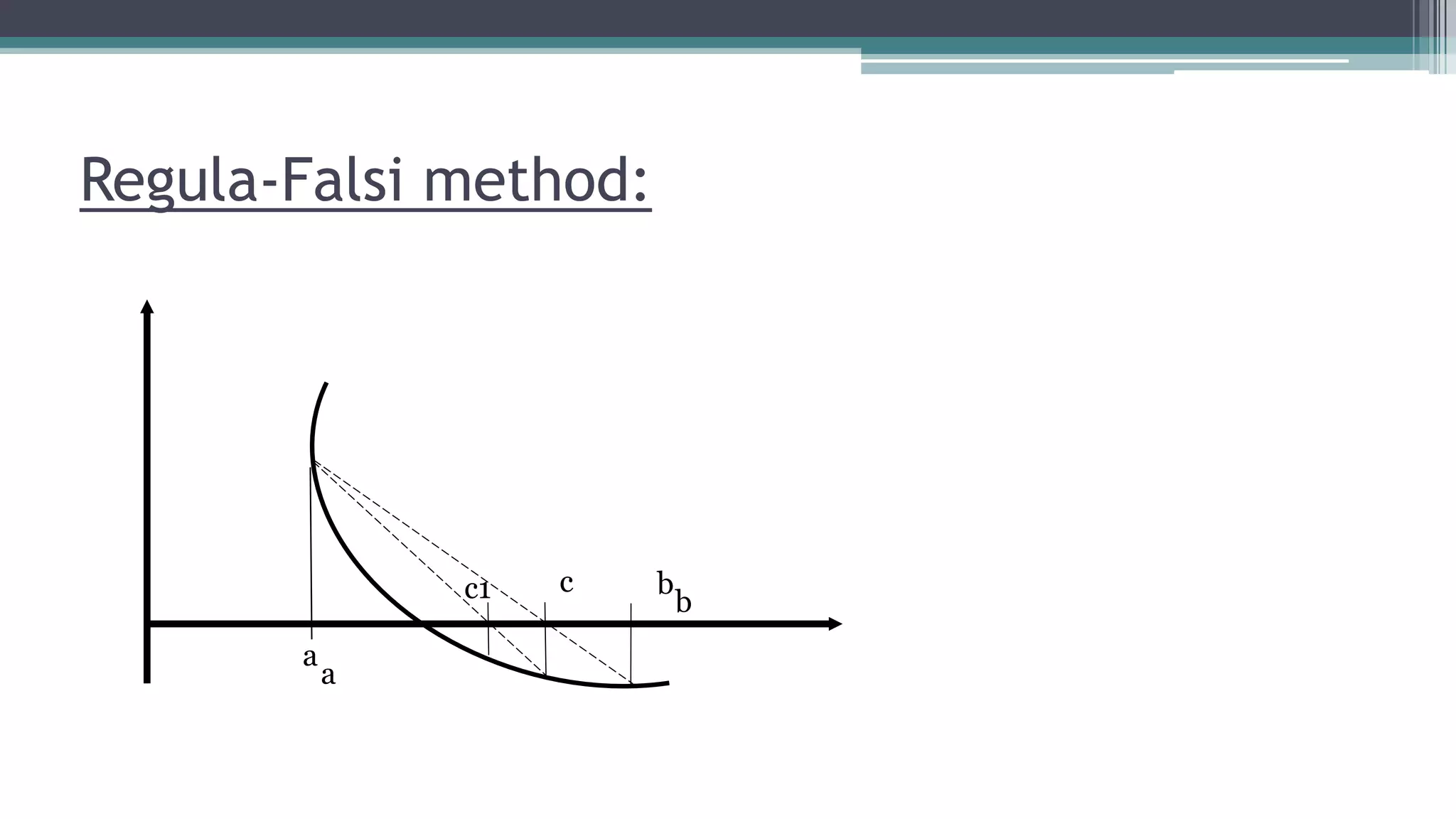
11. Algorithm:
1) Start
2) Read values of x0, x1 and e
*Here x0 and x1 are the two initial guesses
e is the degree of accuracy or the absolute error i.e. the
stopping criteria*
3) Computer function values f(x0) and f(x1)
4) Check whether the product of f(x0) and f(x1) is negative
or
not.
If it is positive take another initial guesses.
If it is negative then goto step 5.
5) Determine:
x = [x0*f(x1) – x1*f(x0)] / (f(x1) – f(x0))

12. 6) Check whether the product of f(x1) and f(x) is
negative or not.
If it is negative, then assign x0 = x;
If it is positive, assign x1 = x;
7) Check whether the value of f(x) is greater than
0.00001 or not.
If yes, goto step 5.
If no, goto step 8.
*Here the value 0.00001 is the desired degree of
accuracy, and hence the stopping criteria.
8) Display the root as x.
9) Stop

13. Example:
Find the root of x * cos[(x)/ (x-2)]=0
Iteration
No.
a b c f(a) * f(c)
1 1 1.5 1.133 0.159 (+ve)
2 1.133 1.5 1.194 0.032 (+ve)
3 1.194 1.5 1.214 3.192E-3 (+ve)
4 1.214 1.5 1.22 2.586E-4(+ve)
5 1.22 1.5 1.222 1.646E-5 (+ve)
6 1.222 1.5 1.222 3.811E-9(+ve)

14. Secant method:
• This method is an improvement over the method of false position
as it doesn’t require the condition
 f(a)*f(b) < 0
• It is same as Regula-falsi method, the equation of finding value of
‘c’ is ,
)()(
)(.)(.
C
afbf
afbbfa




15. Secant method:
a b
c c1

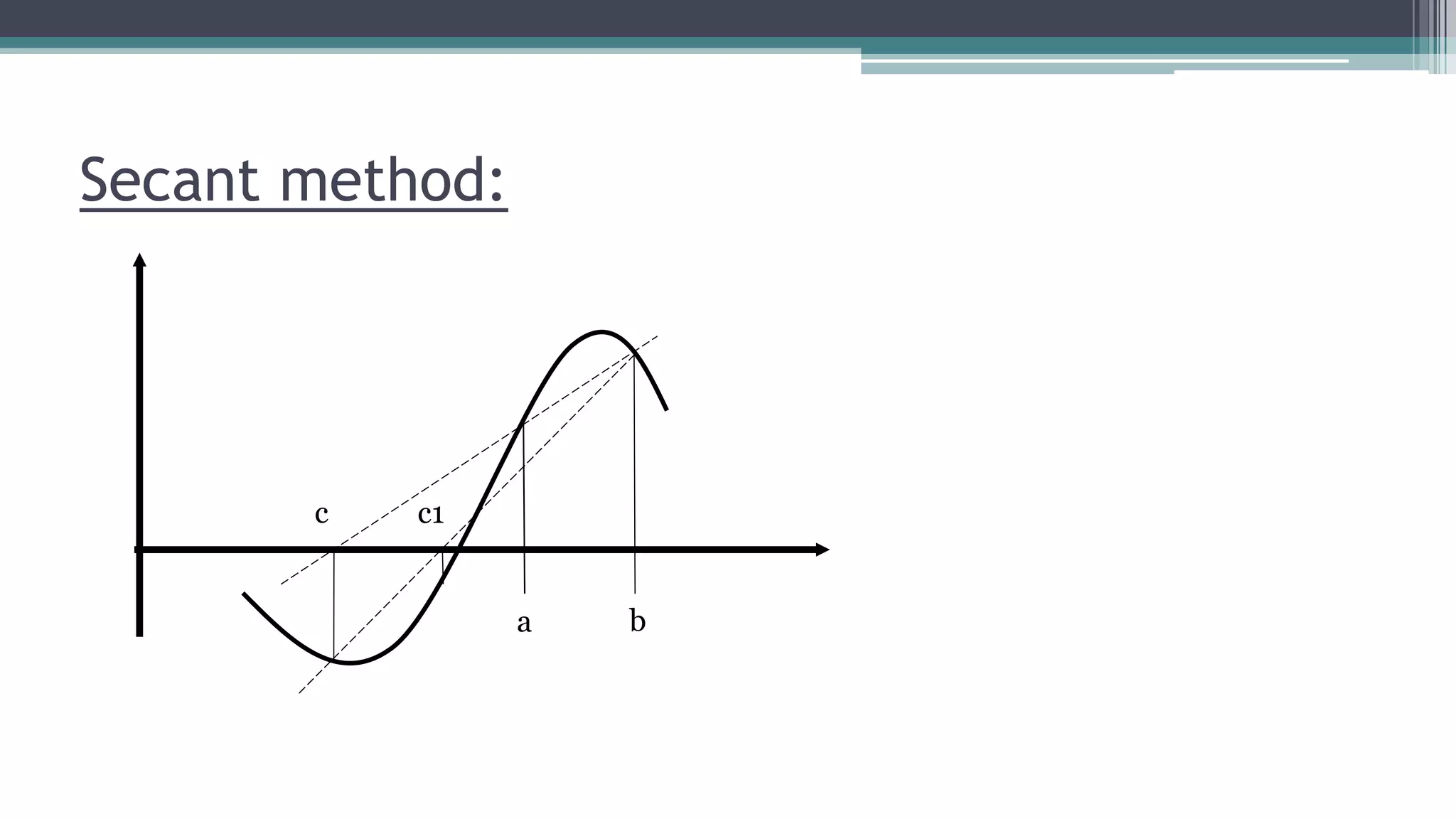
16. Algorithm:
1) Start
2) Read values of x0, x1 and e
*Here x0 and x1 are the two initial guesses
e is the degree of accuracy or the absolute error i.e. the
stopping criteria*
3) Computer function values f(x0) and f(x1)
4) Check whether the product of f(x0) and f(x1) is negative
or
not.
If it is positive take another initial guesses.
If it is negative then goto step 5.
5) Determine:
x = [x0*f(x1) – x1*f(x0)] / (f(x1) – f(x0))

17. 6) No need to check any condition,
Just assign x0 = x1;
assign x1 = x;
7) Check whether the value of f(x) is greater than
0.00001 or not.
If yes, goto step 5.
If no, goto step 8.
*Here the value 0.00001 is the desired degree of
accuracy, and hence the stopping criteria.
8) Display the root as x.
9) Stop

18. Example:

19. Thank You..!!!