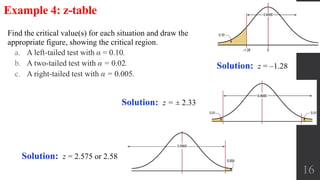
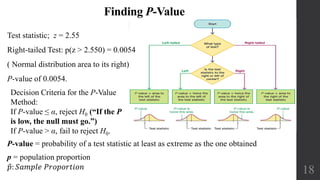
- Hypothesis testing involves evaluating claims about population parameters by comparing a null hypothesis to an alternative hypothesis. - The null hypothesis states that there is no difference or effect, while the alternative hypothesis states that a difference or effect exists. - There are three main methods for hypothesis testing: the critical value method which separates a critical region from a noncritical region, the p-value method which calculates the probability of obtaining a test statistic at least as extreme as the sample test statistic assuming the null is true, and the confidence interval method which rejects claims not included in the confidence interval. - The steps of hypothesis testing are to state the hypotheses, calculate the test statistic, find the critical value, make a decision to reject

1. Elementary Statistics
Chapter 8:
Hypothesis Testing
8.1 Basics of
Hypothesis Testing
1

2. Chapter 8: Hypothesis Testing
8.1 Basics of Hypothesis Testing
8.2 Testing a Claim about a Proportion
8.3 Testing a Claim About a Mean
8.4 Testing a Claim About a Standard Deviation or Variance
2
Objectives:
• Understand the definitions used in hypothesis testing.
• State the null and alternative hypotheses.
• State the steps used in hypothesis testing.
• Test proportions, using the z test.
• Test means when  is known, using the z test.
• Test means when  is unknown, using the t test.
• Test variances or standard deviations, using the chi-square test.
• Test hypotheses, using confidence intervals.

3. Point estimate of p: 𝑝 =
𝑈𝐶𝐿+𝐿𝐶𝐿
2
, UCL: Upper Confidence Limit
Margin of error: 𝐸 =
𝑈𝐶𝐿−𝐿𝐶𝐿
2
, LCL: Lower Confidence Limit
Margin of Error & Confidence Interval for Estimating a Population
Proportion p & Determining Sample Size:
When data from a simple random sample are used to estimate a population
proportion p, the margin of error (maximum error of the estimate ),
denoted by E, is the maximum likely difference (with probability 1 – α, such
as 0.95) between the observed (sample) proportion 𝑝 and the true value of
the population proportion p.
3
ˆ
ˆ ˆ
p E
p E p p E

    2 2
ˆ ˆ ˆ ˆ
ˆ ˆ   
pq pq
p z p p z
n n
 
Recall: 7.1 Estimating a Population Proportion
2
ˆ ˆpq
E z
n

2
2
2
ˆ ˆ( )z pq
n
E


2
2
2
( ) 0.25z
n
E

When no estimate of 𝒑
is known: 𝒑 = 𝒒 =0.5
Determine the sample
size n required to
estimate the value of a
population proportion p
TI Calculator:
Confidence Interval:
proportion
1. Stat
2. Tests
3. 1-prop ZINT
4. Enter: x, n & CL

4. 4
Recall: 7.2 Estimating a Population Mean
Determine the sample size n required to estimate the
value of a population mean µ.
Confidence Interval for Estimating a Population Mean
2
2  
  
 
z
n
E
 
2 2
   
      
   
X z X z
n n
 
 

𝐶𝐼: 𝑥 ± 𝐸 →
2E z
n

 
  
 
2
s
E t
n

 
  
 
2 2
   
      
   
s s
X t X t
n n
 
Confidence Interval for Estimating a Population Mean with σ un Known
Point estimate of µ: 𝑥 =
𝑈𝐶𝐿+𝐿𝐶𝐿
2
, UCL: Upper Confidence Limit
Margin of error: 𝐸 =
𝑈𝐶𝐿−𝐿𝐶𝐿
2
,LCL: Lower Confidence Limit
σ Known
TI Calculator:
Z - interval
1. Stat
2. Tests
3. Z - Interval
4. Enter Data or Stats
( 𝒙 , s & CL)
TI Calculator:
T- Distribution: find the t-score
1. 2nd + VARS
2. invT(
3. 2 entries (Left Area,df)
4. Enter
TI Calculator:
T- interval
1. Stat
2. Tests
3. T - Interval
4. Enter Data or Stats
( 𝒙 , s & CL)
5. Enter

5. Critical Values of χ² We denote a right-tailed critical value by χR
² and we denote a left-tailed critical value
by χL
². Those critical values can be found by using technology or χ² -Table.
Degrees of Freedom: df = n − 1
As the number of degrees of freedom increases, the chi-square distribution approaches a normal
distribution.
Not symmetric: Confidence interval estimate of σ² does not fit a format of
s² − E < σ² < s² + E, so we must do separate calculations for the upper and lower confidence interval limits.
Critical value of χ² in the body of the table corresponds to an area given in the top row of the table, and
each area in that top row is a cumulative area to the right of the critical value.
5
Recall: 7.3 Estimating a Population Standard Deviation or Variance, Chi-Square Distribution
2 2
2
2 2
right left
( 1) ( 1)
, d.f. = 1
n s n s
n
 
 
  
2 2
2 2
right left
( 1) ( 1)
, d.f. = 1
n s n s
n
 
 
  

6. Key Concept: Key components of a formal hypothesis test. The concepts in this section are general and
apply to hypothesis tests involving proportions, means, or standard deviations or variances.
Hypothesis: In statistics, a hypothesis is a claim or statement about a property of a population.
Hypothesis Test: A hypothesis test (or test of significance) is a procedure for testing a claim about a
property of a population.
Researchers are interested in answering many types of questions. For example,
 Is the earth warming up?
 Does a new medication lower blood pressure?
 Does the public prefer a certain color in a new fashion line?
 Is a new teaching technique better than a traditional one?
 Do seat belts reduce the severity of injuries?
These types of questions can be addressed through statistical hypothesis testing, which is a decision-
making process for evaluating claims about a population.
8.1 Basics of Hypothesis Testing
6

7. 1009 consumers were asked if they are comfortable with having drones deliver
their purchases, and 54% (or 545) of them responded with “no.” Using p to
denote the proportion of consumers not comfortable with drone deliveries, the
“majority” claim is equivalent to the claim that the proportion is greater than
half, or p > 0.5. The expression p > 0.5 is the symbolic form of the original
claim.
Example 1
The Claim: The population proportion p; p > 0.5.
Among 1009 consumers, how many do we need to get a significantly high number who
are not comfortable with drone delivery?
A result of 506 (or 50.1%) is just barely more than half, so 506 is clearly not
significantly high.
A result of 1006 (or 99.7%) is clearly significantly high.
What about the result of 545 (or 54.0%)?
Is 545 (or 54.0%) significantly high? The method of hypothesis testing allows us to
answer that key question.
7

8. 8.1 Basics of Hypothesis Testing
A statistical hypothesis is a conjecture (assumption) about a population
parameter. This conjecture may or may not be true.
The null hypothesis, symbolized by H0, is a statistical hypothesis that states that
there is no difference between a parameter and a specific value, or that there is
no difference between two parameters.
(It states that the value of a population parameter such as proportion, mean, or
standard deviation is equal to some claimed value.)
The alternative hypothesis, symbolized by H1 , or Ha ,or HA , is a statistical
hypothesis that states the existence of a difference between a parameter and a
specific value, or states that there is a difference between two parameters.
(It states that the parameter has a value that somehow differs from the null
hypothesis. the symbolic form of the alternative hypothesis: <, >, ≠)
8

9. a. A researcher is interested in
finding out whether a new
medication will have a side
effect on the pulse rate of the
patients who take the
medication. Will the pulse
rate increase, decrease, or
remain unchanged after a
patient takes the medication?
The researcher knows that the
mean pulse rate for the
population under study is 82
beats per minute.
Example 2: Identify the null and alternative Hypotheses.
H0 : 𝜇 = 82 H1 : 𝜇 ≠ 82
This is called a two-tailed
(2TT) hypothesis test.
9
b. A chemist invents
an additive to
increase the life of an
automobile battery.
The mean lifetime of
the automobile
battery without the
additive is 36 months.
H0 : 𝜇 = 36 H1 : 𝜇 > 36
This is called a Right-tailed
(RTT) hypothesis test.
c. A contractor wishes
to lower heating bills
by using a special
type of insulation in
houses. If the average
of the monthly
heating bills is $78,
her hypotheses about
heating costs with the
use of insulation are
H0 : 𝜇 = 78 H1 : 𝜇 < 78
This is called a Left-tailed
(LTT) hypothesis test.

10. 1. The traditional method (Critical Value Method) (CV)
The critical value-Method, separates the critical region from the noncritical region.
2. The P-value method
P-Value Method: In a hypothesis test, the P-value is the probability of getting a value of the test statistic
that is at least as extreme as the test statistic obtained from the sample data, assuming that the null hypothesis
is true.
3. The confidence interval (CI)method
Because a confidence interval estimate of a population parameter contains the likely values of that parameter,
reject a claim that the population parameter has a value that is not included in the confidence interval.
Equivalent Methods: A confidence interval estimate of a proportion might lead to a conclusion different
from that of a hypothesis test.
8.1 Basics of Hypothesis Testing: Three methods used to test hypotheses:
10
Construct a confidence interval with
a confidence level selected:
Significance Level for
Hypothesis Test: α
Two-Tailed Test:
1 – α
One-Tailed
Test: 1 – 2α
0.01 99% 98%
0.05 95% 90%
0.10 90% 80%

11. Procedure for Hypothesis Tests
11
Step 1 State the null and alternative
hypotheses and identify the claim (H0 , H1).
Step 2 Test Statistic (TS): Compute
the test statistic value that is relevant to
the test and determine its sampling
distribution (such as normal, t, χ²).
Step 3 Critical Value (CV) :
Find the critical value(s) from the appropriate
table.
Step 4 Make the decision to
a. Reject or not reject the null
hypothesis.
b. The claim is true or false
c. Restate this decision: There is / is
not sufficient evidence to support
the claim that…

12. In some texts Claim: Use the Original Claim to Create a Null Hypothesis H0 and
an Alternative Hypothesis H1
When a researcher conducts a study, he or she is generally looking for evidence to
support a claim. A claim can be stated as either the null hypothesis or the
alternative hypothesis.
After stating the hypotheses, the researcher’s next step is to design the study:
a. The researcher selects the correct statistical test: (such as z, t, χ²).
b. chooses an appropriate level of significance: α
c. and formulates a plan for conducting the study: CV method, P-value method, CI
(Confidence Interval) method
A statistical test uses the data obtained from a sample to make a decision about
whether the null hypothesis should be rejected. The numerical value obtained from a
statistical test is called the test statistic (value).
The null hypothesis may or may not be true, and a decision is made to reject or not to
reject it on the basis of the data obtained from a sample.
8.1 Basics of Hypothesis Testing
12

13. Type I and Type II Errors
Type I error: The mistake of rejecting the null hypothesis when it is actually true. The symbol α
(alpha) is used to represent the probability of a type I error. (A type I error occurs if one rejects the null
hypothesis when it is true.)
The level of significance is the maximum probability of committing a type I error: α = P(type I
error) = P(rejecting H0 when H0 is true) and Typical significance levels are: 0.10, 0.05, and 0.01
For example, when  = 0.10, there is a 10% chance of rejecting a true null hypothesis.
Type II error: The mistake of failing to reject the null hypothesis when it is actually false. The symbol
β (beta) is used to represent the probability of a type II error. (A type II error occurs if one does not
reject the null hypothesis when it is false.) β = P(type II error) = P(failing to reject H0 when H0 is
false)
13
Preliminary
Conclusion
True State of Nature
Null hypothesis is true
True State of Nature
Null hypothesis is false
Reject H0 Type I error (False
Positive):
Reject a true H0.
P(type I error) = α
Correct decision
(Power of the test)
1 ‒ β
Fail to
reject H0
Correct decision
1 ‒ α
Type II error (False Negative):
Fail to reject a false H0.
P(type II error) = β
8.1 Basics of Hypothesis Testing

14. The critical value, C.V., separates the critical region
from the noncritical region.
The critical or rejection region is the range of values of
the test value that indicates that there is a significant
difference and that the null hypothesis should be
rejected.
The noncritical or nonrejection region is the range of
values of the test value that indicates that the difference
was probably due to chance and that the null hypothesis
should not be rejected.
Two-tailed test: The critical region is in the two extreme
regions (tails) under the curve.
Left-tailed test: The critical region is in the extreme left
region (tail) under the curve.
Right-tailed test: The critical region is in the extreme right
region (tail) under the curve.
14
8.1 Basics of Hypothesis Testing, Two-Tailed (2TT), Left-Tailed (LTT), Right-Tailed (RTT)

15. a. Finding the Critical Value for
α = 0.01 (Right-Tailed Test)
b. Finding the Critical Value for
α = 0.01 (Left-Tailed Test)
c. Finding the Critical Value for
α = 0.01 (Two-Tailed Test)
Example 3: z-table
15
z = 2.33 for α = 0.01 (RTT)
Because of symmetry,
z = –2.33 for α = 0.01 (LTT)
z = ±2.575

16. Find the critical value(s) for each situation and draw the
appropriate figure, showing the critical region.
a. A left-tailed test with α = 0.10.
b. A two-tailed test with α = 0.02.
c. A right-tailed test with α = 0.005.
Example 4: z-table
Solution: z = –1.28
16
Solution: z = 2.575 or 2.58
Solution: z = ± 2.33

17. Identify the test statistic that is relevant to the test and determine its
sampling distribution (such as z, t, χ²)
17
Parameter
Sampling
Distribution
Requirements Test Statistics
Proportion:
p
Normal (Z) 𝑛𝑝 ≥ 5, & 𝑛𝑞 ≥ 5
𝑍 =
𝑝 − 𝑝
𝑝𝑞/𝑛
Mean: 𝝁 t 𝝈 not known & Normally
Distributed Population or
𝑛 > 30
𝑡 =
𝑥 − 𝜇
𝑠/ 𝑛
Mean: 𝝁 Normal (Z) 𝝈 known & Normally
Distributed Population or
𝑛 > 30
𝑍 =
𝑥 − 𝜇
𝜎/ 𝑛
Standard
Deviation: 𝝈
Or Variance: 𝝈 𝟐
𝝌 𝟐 Normally Distributed
Population 𝜒2
=
(𝑛 − 1)𝑠2
𝜎2

18. Finding P-Value
18
P-value = probability of a test statistic at least as extreme as the one obtained
p = population proportion
𝑝: 𝑆𝑎𝑚𝑝𝑙𝑒 𝑃𝑟𝑜𝑝𝑜𝑟𝑡𝑖𝑜𝑛
Test statistic; z = 2.55
Right-tailed Test: p(z > 2.550) = 0.0054
( Normal distribution area to its right)
P-value of 0.0054.
Decision Criteria for the P-Value
Method:
If P-value ≤ α, reject H0 (“If the P
is low, the null must go.”)
If P-value > α, fail to reject H0.

19. Example 6: Describing Type I and Type II Errors
Consider the claim that a medical procedure designed to increase the likelihood of a baby girl is effective, so that
the probability of a baby girl is p > 0.5. Given the following null and alternative hypotheses, write statements
describing a) type I error, and (b) a type II error.
(HINT FOR DESCRIBING TYPE I AND TYPE II ERRORS: Descriptions of a type I error and a
type II error refer to the null hypothesis being true or false, but when wording a statement representing
a type I error or a type II error, be sure that the conclusion addresses the original claim (which may
or may not be the null hypothesis).
H0: p = 0.5
H1: p > 0.5 (original claim that will be addressed in the final conclusion)
19
Solution
a. Type I Error: A type I error is the mistake of rejecting a true null hypothesis, so
the following is a type I error: In reality p = 0.5, but sample evidence leads us to
conclude that p > 0.5. (In this case, a type I error is to conclude that the medical
procedure is effective when in reality it has no effect.)
b. Type II Error: A type II error is the mistake of failing to reject the null hypothesis
when it is false, so the following is a type II error: In reality p > 0.5, but we fail to
support that conclusion. (In this case, a type II error is to conclude that the
medical procedure has no effect, when it really is effective in increasing the
likelihood of a baby girl.)