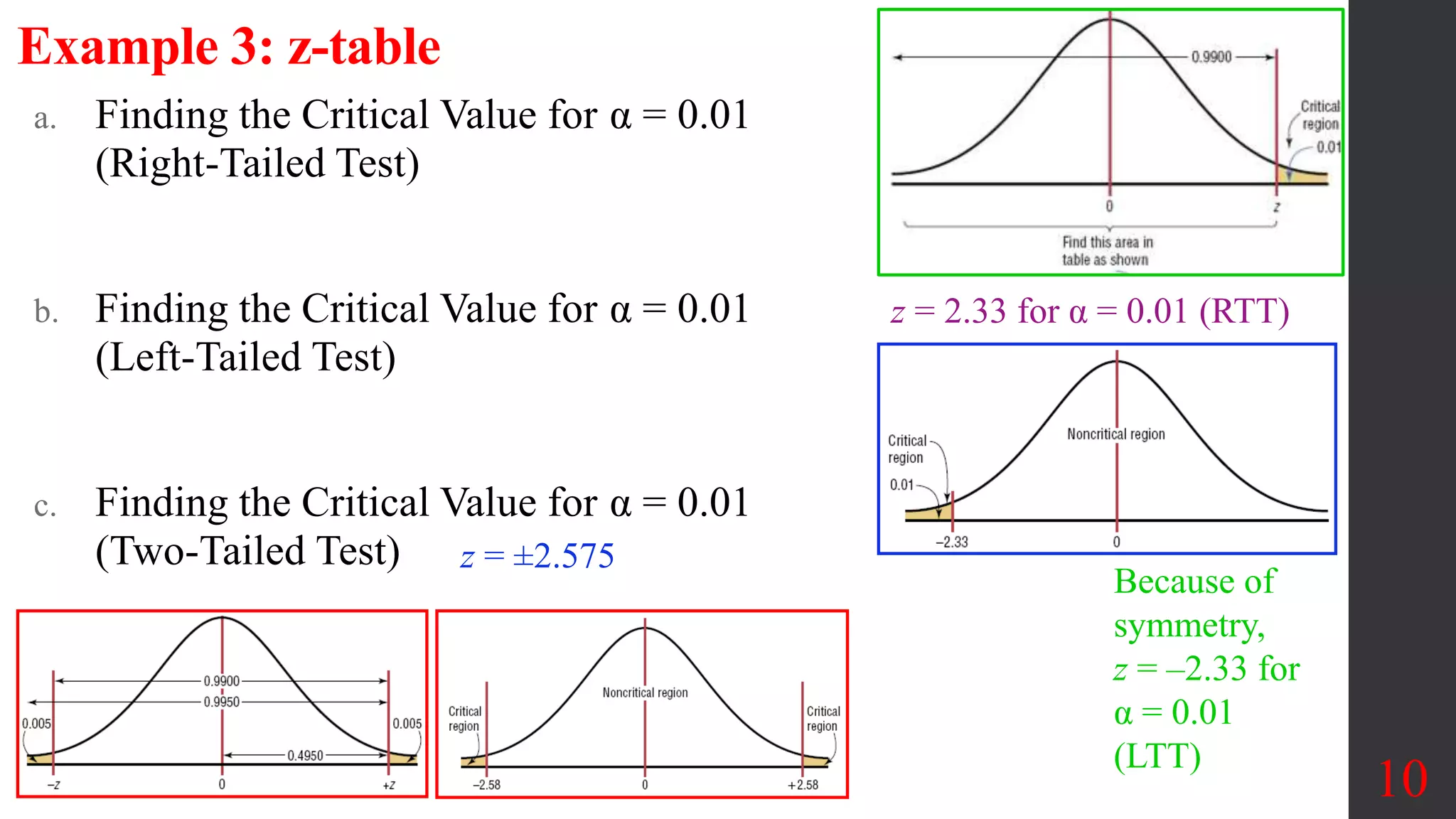
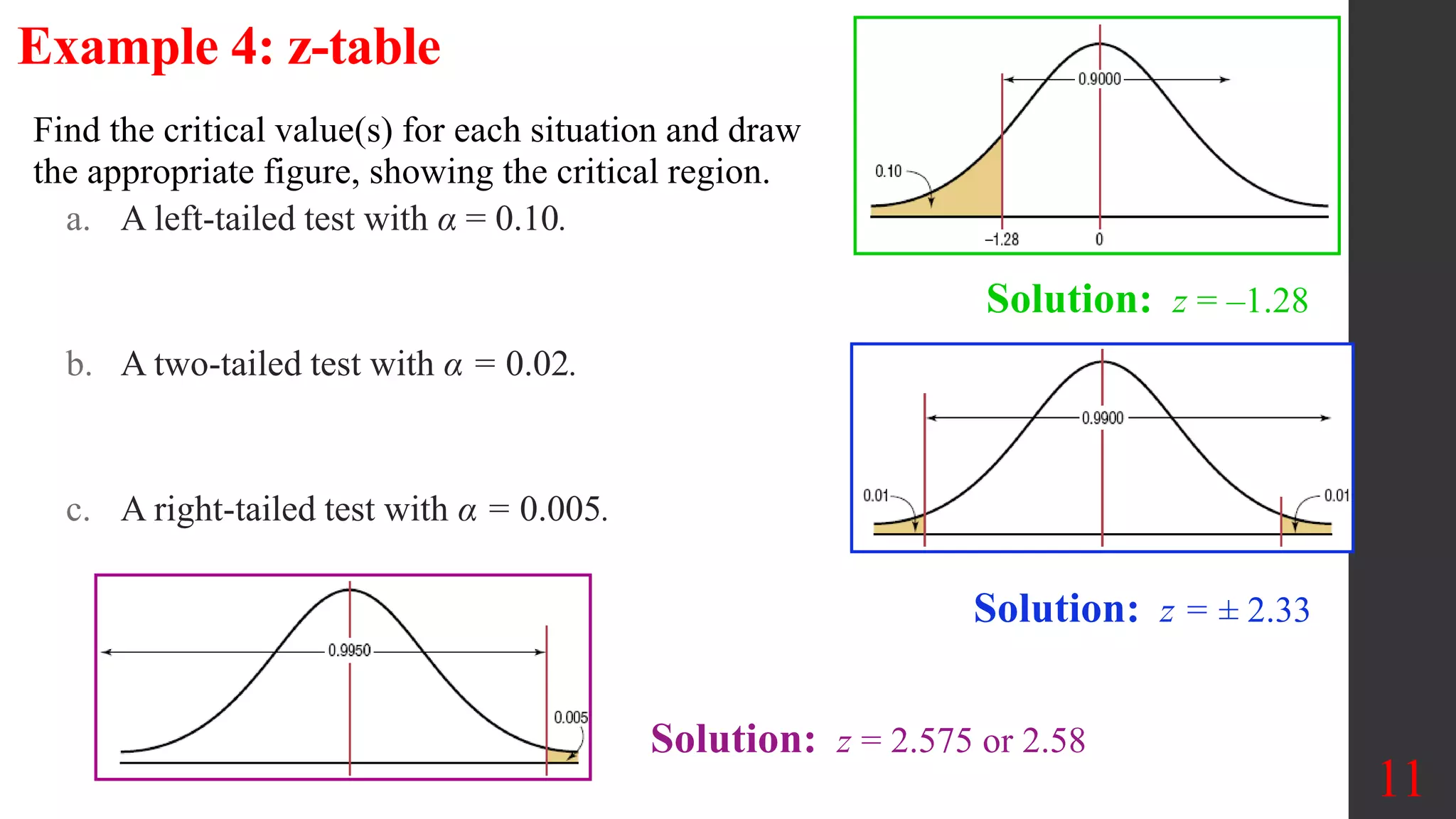
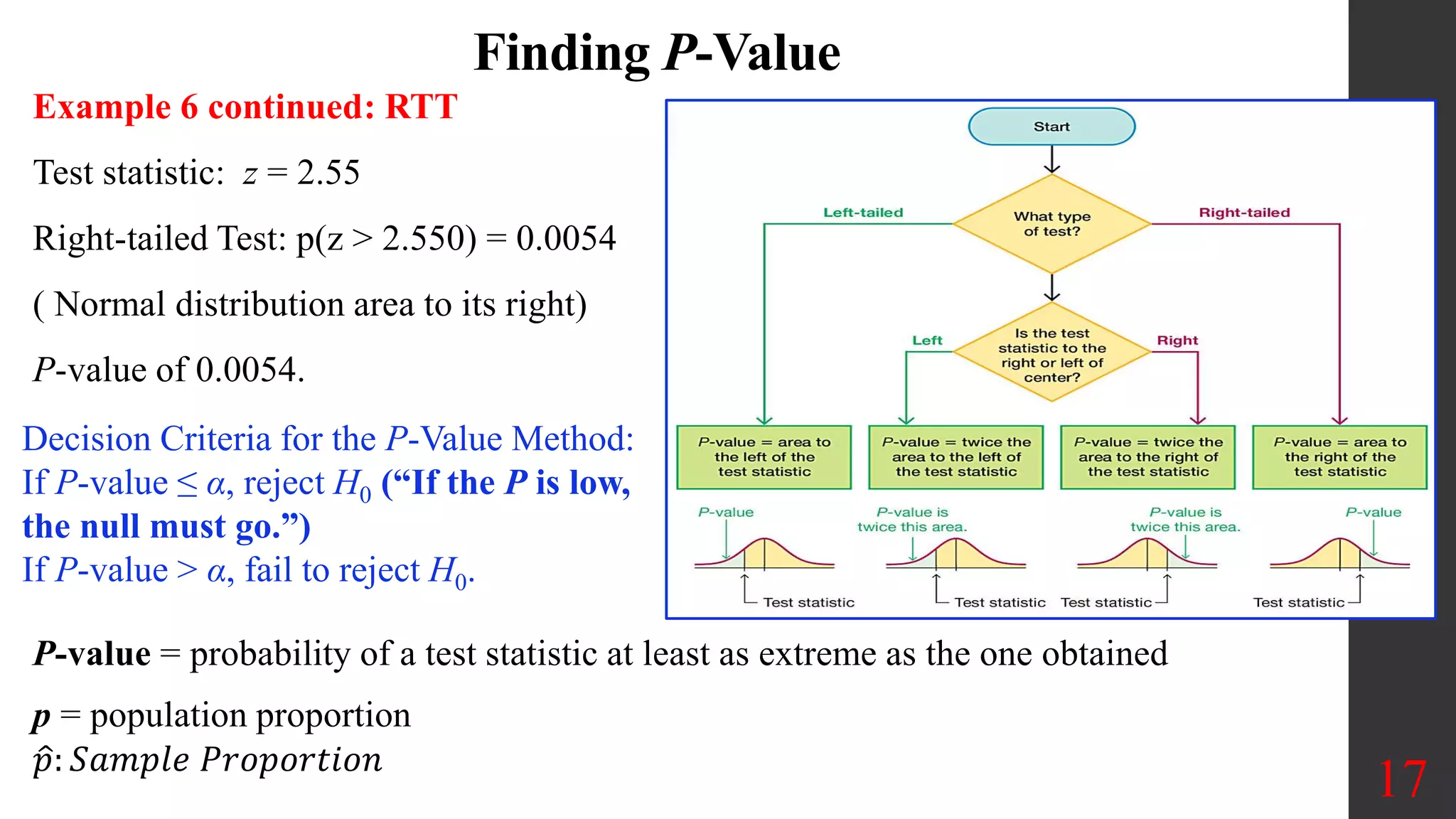
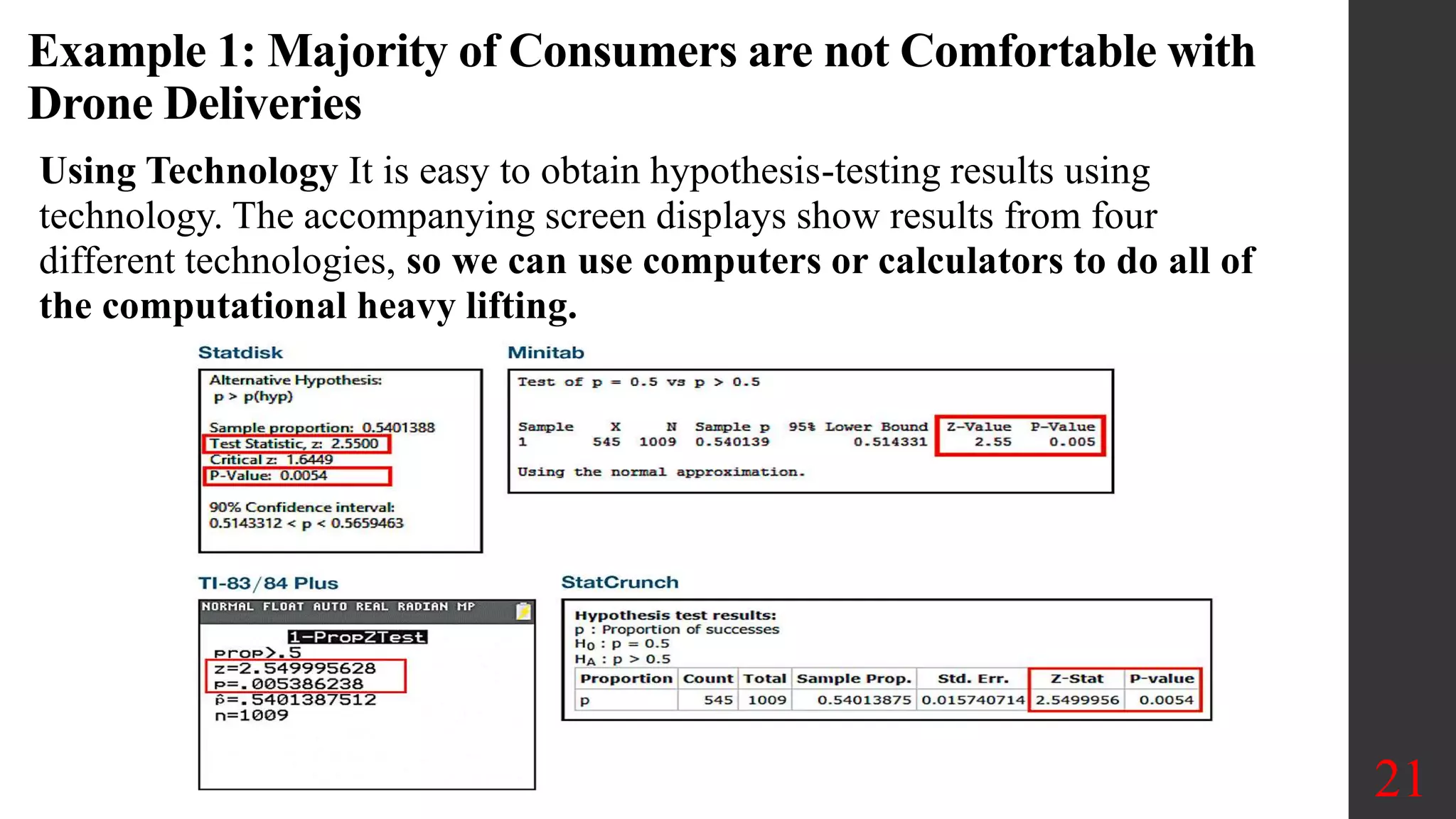
Chapter 8 of the document covers the basics of hypothesis testing, outlining the definitions of null and alternative hypotheses, various statistical tests for proportions, means, and variances, as well as error types and decision-making processes. It emphasizes the importance of the critical region and the p-value method for evaluating claims about population parameters, along with examples illustrating different test scenarios. Key concepts such as Type I and Type II errors, significance levels, and the power of tests are also discussed.