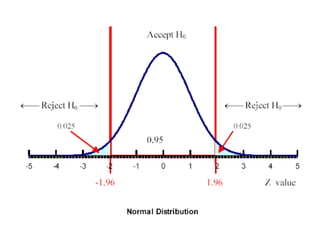
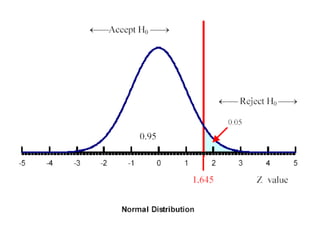
This document discusses one-tailed and two-tailed hypothesis tests. A one-tailed test has rejection regions in only one tail, while a two-tailed test splits rejection regions equally between both tails. The key difference is how the null and alternative hypotheses are expressed. A one-tailed alternative hypothesis uses "<" or ">" to specify the direction of the expected difference, while a two-tailed alternative uses "≠" to allow for differences in either direction. The appropriate type of test depends on what the researcher aims to prove.

1. One-Sided or One-Tailed Hypothesis Tests
In most applications, a two-sided or two-tailed hypothesis test
is the most appropriate approach. This approach is based on
the expression of the null and alternative hypotheses as
follows:
H0: = 170 vs H1: ≠ 170
To test the above hypothesis, we set up the rejection and
acceptance regions as shown on the next slide, where we are
using = 0.05.

2. Accept H0
Reject H0 Reject H0
0.025
0.95 0.025
Z

3. In this example, the rejection region
probabilities are equally split between the two
tails, thus the reason for the label as a two-
tailed test.
This procedure allows the possibility of
rejecting the null hypothesis, but does not
specifically address, in the sense of statistical
significance, the direction of the difference
detected.

4. The difference between the two has to do with how
the null hypothesis is expressed and the implication
of this expression.
The first expression above is the more theoretically
correct one and carries with it the clear connotation
that an outcome in the opposite direction of the
alternative hypothesis is not considered possible.
This is, in fact, the way the test is actually done.

5. The process of testing the above hypothesis is
identical to that for the two-tailed test except that
all the rejection region probabilities are in one tail.
For a test, with α = 0.05, the acceptance region
would be, for example, the area from the extreme
left up to the point below which lies 95% of the
area.
The rejection region would be the 5% area in the
upper tail.

7. The Experiment
• For 40 randomly selected customers who order a
pepperoni pizza for home delivery, he includes both
an old style and a free new style pizza in the order.
• All he asks is that these customers rate the difference
between pizzas on a -10 to +10 scale, where -10
means they strongly favor the old style, +10 means
they strongly favor the new style, and 0 means they
are indifferent between the two styles.
Old pizza New pizza
-10 0 +10

8. 1. Formulate H1and H0
One-Tailed Versus Two-Tailed Tests
• The form of the alternative hypothesis can be either a
one-tailed or two-tailed, depending on what you are
trying to prove.
• A one-tailed hypothesis is one where the only sample
results which can lead to rejection of the null hypothesis
are those in a particular direction, namely, those where
the sample mean rating is positive.
• A two-tailed test is one where results in either of two
directions can lead to rejection of the null hypothesis.

9. 1. Formulate H1and H0
One-Tailed Versus Two-Tailed Tests -- continued
• Once the hypotheses are set up, it is easy to detect
whether the test is one-tailed or two-tailed.
• One tailed alternatives are phrased in terms of “>” or
“<“ whereas two tailed alternatives are phrased in
terms of “ ”
• The real question is whether to set up hypotheses for
a particular problem as one-tailed or two-tailed.
• There is no statistical answer to this question. It
depends entirely on what we are trying to prove.

10. 1. Formulate H1and H0
• As the manager you would like to observe a
difference between both pizzas
• If the new baking method is cheaper, you would
like the preference to be for it.
– Null Hypothesis –H0 =0 (there is no difference
between the old style and the new
style pizzas) (The difference between
the mean of the sample and the mean
of the population is zero)
– Alternative H1 0 or H1 >0
Two tail One tail
test test
= mu=population mean