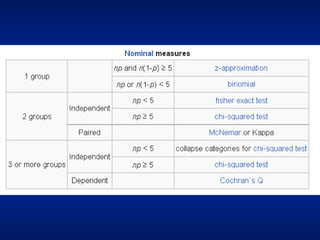
This document discusses key concepts in research methods and biostatistics, including hypothesis testing, random error, p-values, and confidence intervals. It explains that hypothesis testing involves determining if study findings reflect chance or a true effect. The p-value represents the probability of observing results as extreme or more extreme than what was observed by chance alone. A p-value less than 0.05 indicates statistical significance. Confidence intervals provide a range of values that are likely to contain the true population parameter.

1. Introduction to Research Methods
In the Internet Era
Introduction to Biostatistics
Inferential Statistics
Hypothesis Testing
Thomas Songer, PhD
with acknowledgment to several slides provided by
M Rahbar and Moataza Mahmoud Abdel Wahab

2. Key Lecture Concepts
• Assess role of random error (chance) as an
influence on the validity of the statistical
association
• Identify role of the p-value in statistical
assessments
• Identify role of the confidence interval in
statistical assessments
• Briefly introduce tests to undertake
2

3. Research Process
Research question
Hypothesis
Identify research design
Data collection
Presentation of data
Data analysis
Interpretation of data
Polgar, Thomas 3

4. Interpreting Results
When evaluating an association between
disease and exposure, we need guidelines
to help determine whether there is a
true difference in the frequency of disease
between the two exposure groups, or perhaps
just random variation from the study sample.
4

5. Random Error (Chance)
1. Rarely can we study an entire population, so
inference is attempted from a sample of
the population
2. There will always be random variation
from sample to sample
3. In general, smaller samples have less
precision, reliability, and statistical power
(more sampling variability)
5

6. Hypothesis Testing
• The process of deciding statistically
whether the findings of an
investigation reflect chance or real
effects at a given level of probability.
6

7. Elements of Testing hypothesis
• Null Hypothesis
• Alternative hypothesis
• Identify level of significance
• Test statistic
• Identify p-value / confidence interval
• Conclusion
7

8. H0: There is no association between the
exposure and disease of interest
H1: There is an association between the
exposure and disease of interest
8
Hypothesis Testing
Note: With prudent skepticism, the null hypothesis
is given the benefit of the doubt until the data
convince us otherwise.

9. Hypothesis Testing
• Because of statistical uncertainty regarding
inferences about population parameters based
upon sample data, we cannot prove or
disprove either the null or alternate
hypotheses as directly representing the
population effect.
• Thus, we make a decision based on
probability and accept a probability of
making an incorrect decision.
Chernick 9

10. Associations
• Two types of pitfalls can occur that
affect the association between
exposure and disease
–Type 1 error: observing a difference
when in truth there is none
–Type 2 error: failing to observe a
difference where there is one.
10

11. Interpreting Epidemiologic Results
Four possible outcomes of any epidemiologic study:
YOUR
DECISION
H0 True
(No assoc.)
H1 True
(Yes assoc.)
Do not reject H0
(not stat. sig.)
Correct
decision
Type II
(beta error)
Reject H0
(stat. sig.)
Type I
(alpha error)
Correct
decision
11
REALITY

12. Four possible outcomes of any epidemiologic study:
YOUR
DECISION
H0 True
(No assoc.)
H1 True
(Yes assoc.)
Do not reject H0
(not stat. sig.)
Correct
decision
Failing to find a
difference when
one exists
Reject H0
(stat. sig.)
Finding a
difference when
there is none
Correct decision
12
REALITY

13. Type I and Type II errors
"a is the probability of committing type I
error.
"b is the probability of committing type II
error.
13

14. “Conventional” Guidelines:
• Set the fixed alpha level (Type I error) to 0.05
This means, if the null hypothesis is true, the
probability of incorrectly rejecting it is 5% or less.
DECISION H0 True H1 True
Do not reject H0
(not stat. sig.)
Reject H0
(stat. sig.)
Type I
(alpha error)
14
Study Result

15. Empirical Rule
For a Normal distribution approximately,
a) 68% of the measurements fall within one
standard deviation around the mean
b) 95% of the measurements fall within two
standard deviations around the mean
c) 99.7% of the measurements fall within three
standard deviations around the mean
15

16. Normal Distribution
34.13% 34.13%
13.59%
2.28%
13.59%
2.28%
50% 50 %
16
• a usually set at 5%)

17. 4. A test statistic to assess “statistical significance”
is performed to assess the degree to which the
data are compatible with the null hypothesis of no
association
5. Given a test statistic and an observed value, you
can compute the probability of observing a value
as extreme or more extreme than the observed
value under the null hypothesis of no association.
This probability is called the “p-value”
17
Random Error (Chance)

18. Random Error (Chance)
6. By convention, if p < 0.05, then the
association between the exposure and disease is
considered to be “statistically
significant.”
(e.g. we reject the null hypothesis (H0) and
accept the alternative hypothesis (H1))
18

19. Random Error (Chance)
• p-value
– the probability that an effect at least as
extreme as that observed could have
occurred by chance alone, given there is
truly no relationship between exposure and
disease (Ho)
– the probability the observed results
occurred by chance
– that the sample estimates of association
differ only because of sampling variability.
Sever 19

20. What does p < 0.05 mean?
Indirectly, it means that we suspect that the
magnitude of effect observed (e.g. odds ratio) is
not due to chance alone (in the absence of
biased data collection or analysis)
Directly, p=0.05 means that one test result out
of twenty results would be expected to occur
due to chance (random error) alone
20
Random Error (Chance)

21. Example:
D+ D-E+
15 85
E- 10 90
IE+ = 15 / (15 + 85) = 0.15
IE- = 10 / (10 + 90) = 0.10
RR = IE+/IE- = 1.5, p = 0.30
Although it appears that the incidence of disease may be
higher in the exposed than in the non-exposed (RR=1.5),
the p-value of 0.30 exceeds the fixed alpha level of 0.05.
This means that the observed data are relatively
compatible with the null hypothesis. Thus, we do not
reject H0 in favor of H1 (alternative hypothesis).
21

22. Random Error (Chance)
Take Note:
The p-value reflects both the magnitude of the
difference between the study groups AND the
sample size
22
• The size of the p-value does not
indicate the importance of the results
• Results may be statistically significant
but be clinically unimportant
• Results that are not statistically
significant may still be important

23. 23
Sometimes we are more concerned with
estimating the true difference than the
probability that we are making the
decision that the difference between
samples is significant

24. Random Error (Chance)
A related, but more informative, measure known
as the confidence interval (CI) can also be
calculated.
CI = a range of values within which the true
population value falls, with a certain degree of
assurance (probability).
24

25. Confidence Interval - Definition
A range of values for a variable constructed
so that this range has a specified
probability of including the true value of
the variable
A measure of the study’s precision
Lower limit Upper limit
Sever
Point estimate
25

26. Statistical Measures of Chance
• Confidence interval
–95% C.I. means that true estimate of
effect (mean, risk, rate) lies within 2
standard errors of the population
mean 95 times out of 100
Sever 26

27. Interpreting Results
Confidence Interval: Range of values for a point
estimate that has a specified probability of
including the true value of the parameter.
Confidence Level: (1.0 – a), usually expressed
as a percentage (e.g. 95%).
Confidence Limits: The upper and lower end
points of the confidence interval.
27

28. Hypothetical Example of 95% Confidence Interval
Exposure: Caffeine intake (high versus low)
Outcome: Incidence of breast cancer
Risk Ratio: 1.32 (point estimate)
p-value: 0.14 (not statistically significant)
95% C.I.: 0.87 - 1.98
95% confidence interval
_____________________________________________________
0.0 0.5 1.0 1.5 2.0
28
(null value)

29. INTERPRETATION:
Our best estimate is that women with high caffeine
intake are 1.32 times (or 32%) more likely to develop
breast cancer compared to women with low caffeine
intake. However, we are 95% confident that the
true value (risk) of the population lies between
0.87 and 1.98 (assuming an unbiased study).
95% confidence interval
_____________________________________________
0.0 0.5 1.0 1.5 2.0
(null value)
29
Random Error (Chance)

30. If the 95% confidence interval does NOT include
the null value of 1.0 (p < 0.05), then we declare a
“statistically significant” association.
If the 95% confidence interval includes the null
value of 1.0, then the test result is “not statistically
significant.”
30
Random Error (Chance)
Interpretation:

31. Interpretation of C.I. For OR and RR:
The C.I. provides an idea of the likely magnitude of
the effect and the random variability of the point
estimate.
On the other hand, the p-value reveals nothing about
the magnitude of the effect or the random variability
of the point estimate.
In general, smaller sample sizes have larger C.I.’s due
to uncertainty (lack of precision) in the point estimate.
31
Interpreting Results

32. Selection of Tests of
Significance
32

33. Scale of Data
1. Nominal: Data do not represent an amount or
quantity (e.g., Marital Status, Sex)
2. Ordinal: Data represent an ordered series of
relationship (e.g., level of education)
3. Interval: Data are measured on an interval scale
having equal units but an arbitrary zero point. (e.g.:
Temperature in Fahrenheit)
4. Interval Ratio: Variable such as weight for which we
can compare meaningfully one weight versus another
(say, 100 Kg is twice 50 Kg) 33

34. Which Test to Use?
Scale of Data
Nominal Chi-square test
Ordinal Mann-Whitney U test
Interval (continuous)
T-test
- 2 groups
Interval (continuous)
- 3 or more groups
ANOVA
34

37. Tests for distributions
• Common tests
– For nominal data
• with small counts – Fisher’s exact test >fisher.test()
• with all counts >5 – Chi-squared test >chisq.test()
• in case of dependent objects – McNemar test
>mcnemar.test()
– For continuous data
• Kolmogorov-Smirnov test >ks.test()
• Special tests
– Normality tests
• Shapiro-Wilks test >shapiro.test()

38. Tests for locations
• Parametric tests
– One-sample: t-test
>t.test()
– Two-sample, independent
data: t-test >t.test()
– Two-sample, dependent
data: paired t-test
>t.test(…, paired=TRUE)
– Many samples,
independent data:
ANOVA >aov()
– Many samples, dependent
data: repeated
measurements ANOVA
>aov(…, error=…)
• Nonparametric tests
– One-sample: Wilcoxon sign
test >wilcox.test()
– Two-sample, independent
data: Wilcoxon rank-sum
test >wilcox.test()
– Two-sample, dependent
data: Wilcoxon signed-rank
test >wilcox.test(…,
paired=TRUE)
– Many samples, independent
data: Kruskal-Wallis test
>kruskal.test()
– Many samples, dependent
data: Friedman test
>friedman.test()

39. Tests for scales
• Parametric tests
– Two-sample: Fisher’s
test >f.test()
– Many samples:
Bartlett’s test
>bartlett.test()
• Nonparametric tests
– Two-sample: Ansari-
Bradley test
>ansari.test()
– Many samples: Fligner-
Killeen test
>fligner.test()