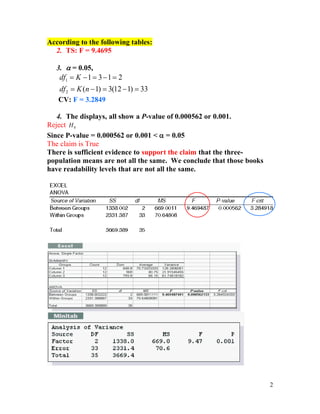
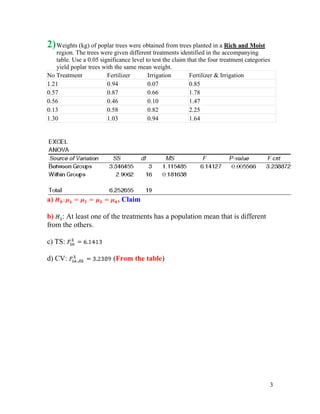
This document summarizes the solutions to three one-way ANOVA problems testing claims about population means. The first problem analyzes readability scores of three books and finds sufficient evidence to reject the claim that the means are all the same. The second problem examines tree weights under different treatments and fails to support the claim that all treatment means are equal. The third problem also looks at tree weights but in a different region, and finds sufficient evidence to fail to reject the claim that all treatment means are the same.

1. 1
Statistics Practice (Sample) Test Solution
Chapter 12: Analysis of Variance
1)(One-Way ANOVA) Given the readability scores summarized in the
following table and a significance level of  = 0.05, use technology to
test the claim that the three samples come from populations with means
that are not all the same.
Clancy Rowling Tolstoy
N 12 12 12
x 70.73 80.75 66.15
S 11.33 4.68 7.86
1.
: At least one of the means is different from the others. Claim
TI Calculator:
One Way ANOVA
1. ClrList ,
2. Enter data ,
3. Stat
4. Tests
5.
6. Enter

2. 2
According to the following tables:
2. TS: F = 9.4695
3.  = 0.05,
1
2
1 3 1 2
( 1) 3(12 1) 33
df K
df K n
= − = − =
= − = − =
CV: F = 3.2849
4. The displays, all show a P-value of 0.000562 or 0.001.
Reject 0
H
Since P-value = 0.000562 or 0.001 <  = 0.05
The claim is True
There is sufficient evidence to support the claim that the three-
population means are not all the same. We conclude that those books
have readability levels that are not all the same.

3. 3
2)Weights (kg) of poplar trees were obtained from trees planted in a Rich and Moist
region. The trees were given different treatments identified in the accompanying
table. Use a 0.05 significance level to test the claim that the four treatment categories
yield poplar trees with the same mean weight.
No Treatment Fertilizer Irrigation Fertilizer & Irrigation
1.21 0.94 0.07 0.85
0.57 0.87 0.66 1.78
0.56 0.46 0.10 1.47
0.13 0.58 0.82 2.25
1.30 1.03 0.94 1.64
a) , Claim
b) : At least one of the treatments has a population mean that is different
from the others.
c) TS:
d) CV: (From the table)

4. 4
e) The p-value is 0.0056
f) Reject 0
H since the p-value = 0.00566 < 05
.
0
=
 .
The claim is False
There is sufficient evidence to reject the claim that and to
conclude that at least one is different.
OR:
There is not sufficient evidence to support the claim that
4
3
2
1 


 =
=
= and to conclude that the four treatments DO Not result in
poplar trees with the same weight.
3)(One-Way ANOVA) Polar Tree Weights: Weights (kg) of poplar trees were
obtained from trees planted in a Sandy and Dry region. The trees were given
different treatments identified in the accompanying table. Use a 0.05 significance
level to test the claim that the four treatment categories yield poplar trees with the
same mean weight.
No Treatment Fertilizer Irrigation Fertilizer & Irrigation

5. 5
0.24 0.92 0.96 1.07
1.69 0.07 1.43 1.63
1.23 0.56 1.26 1.39
0.99 1.74 1.57 0.49
1.80 1.13 0.75 0.95
a) , Claim
b) : At least one of the treatments has a population mean that is different
from the others.
c) TS: 3
16 0.380105
F =
d) CV: 3
16,.05 3.238872
F =
e) The p-value is 0.768664
f) Fail to reject 0
H since the p-value = 0.768664 > 05
.
0
=
 .
The claim is True

6. 6
There is sufficient evidence to support the claim that 4
3
2
1 


 =
=
= and
to conclude that the four treatments results in poplar trees with the same
weight.