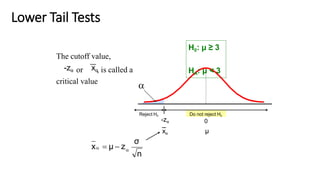
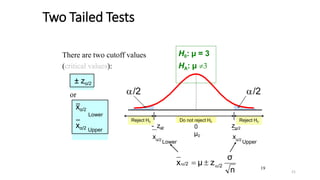
The document provides an introduction to hypothesis testing and statistical inference, outlining key concepts such as population, sample, and parameter. It details the steps involved in hypothesis testing, including forming null and alternative hypotheses, determining significance levels, and identifying errors associated with the decisions made. Additionally, it includes examples of hypothesis tests relevant to various fields, illustrating how to apply these concepts in practical scenarios.