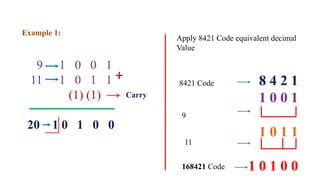
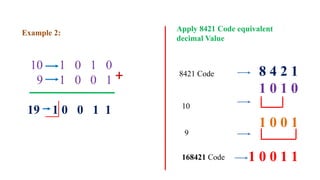
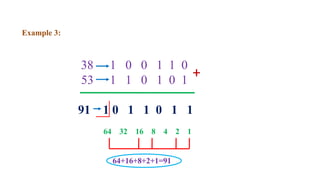
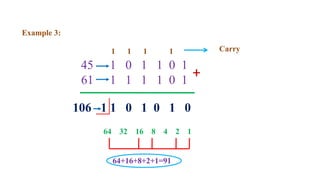
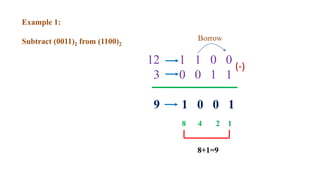
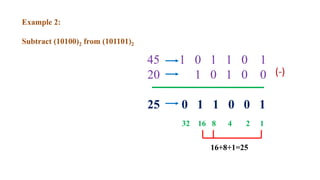
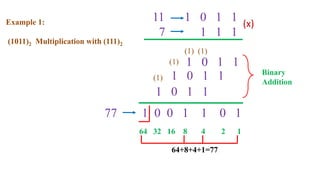
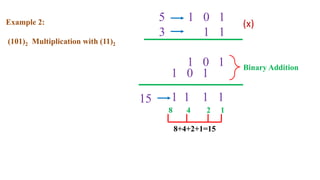
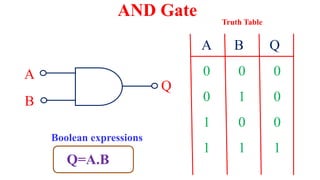
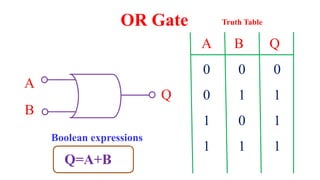
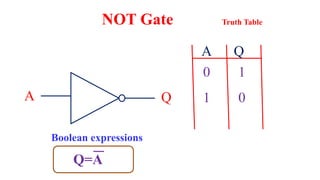
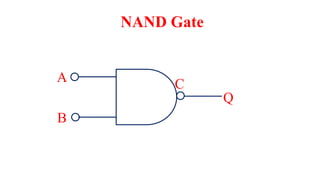
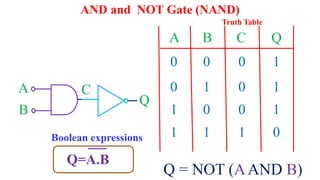
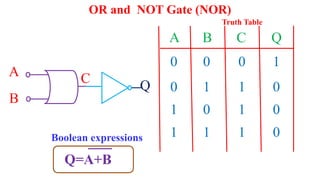
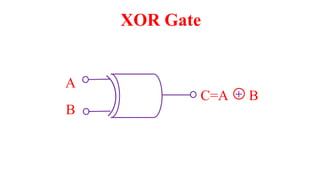
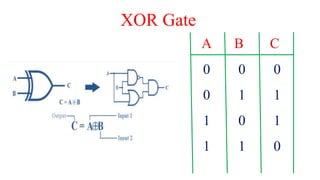
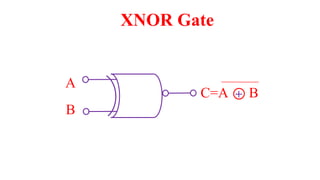
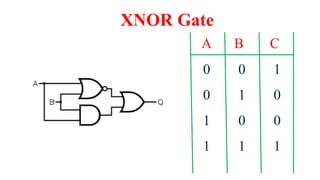
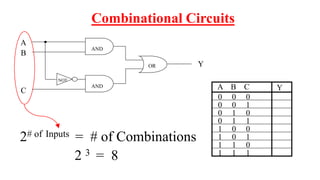
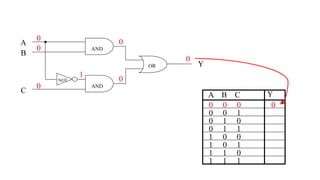
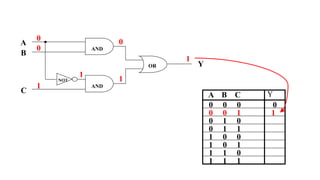
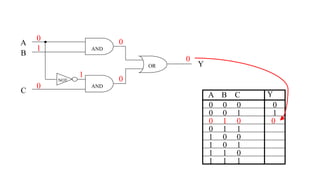
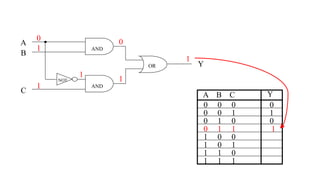
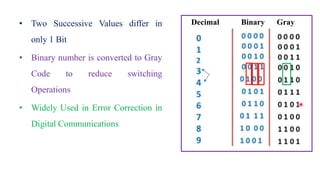
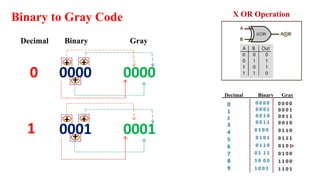
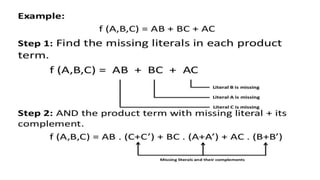
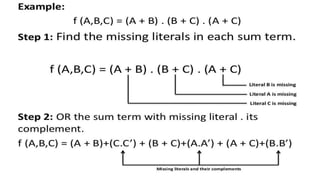
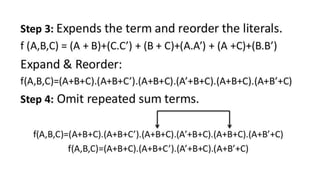
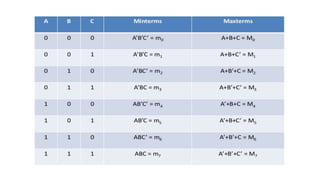
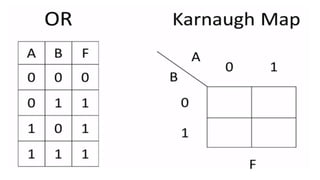
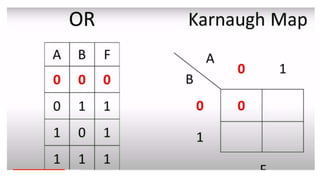
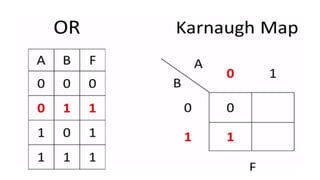
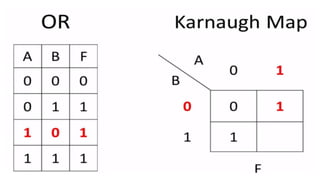
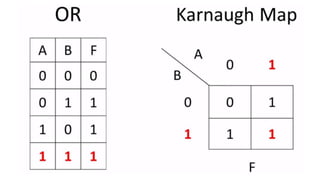
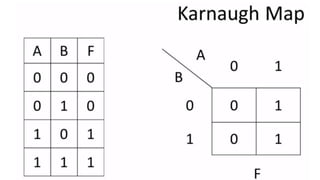
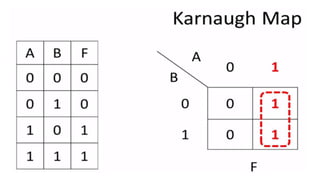
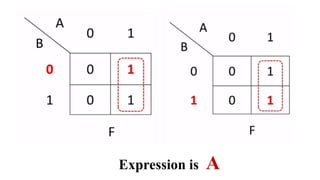
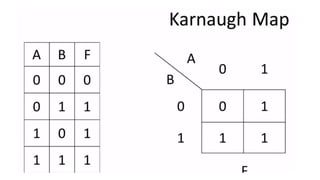
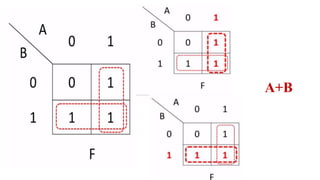
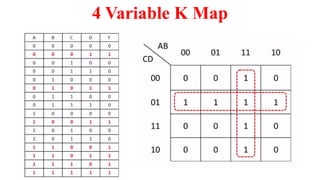
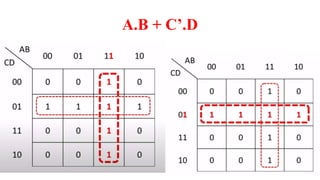
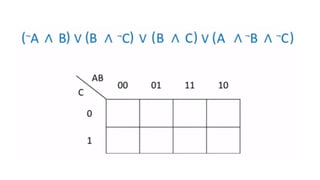
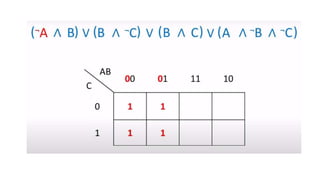
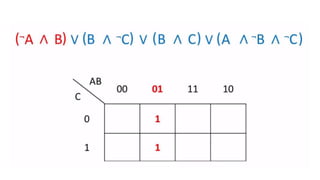
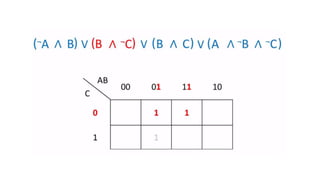
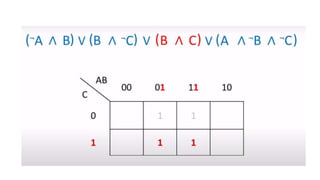
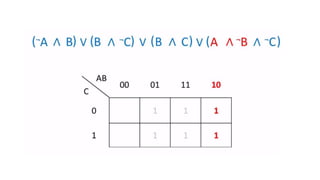
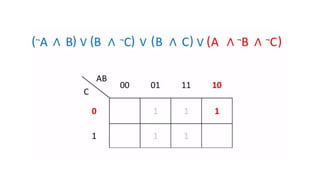
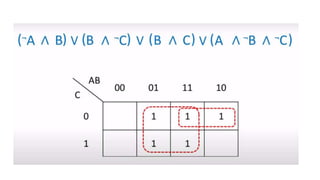
This document outlines the topics covered in the 21EC201 - Digital Principles and System Design course. It includes an introduction to number systems, logic gates, combinational logic circuits, Boolean algebra, truth tables and Karnaugh maps. Specific topics mentioned are binary, decimal, octal and hexadecimal number systems, logic gates like AND, OR, NAND, NOR, XOR and XNOR, arithmetic operations in binary and conversions between different number systems.

1. 21EC201– Digital Principles and System Design

2. UNIT I - DIGITAL FUNDAMENTALS

3. Outline
 Number Systems – Decimal, Binary, Octal, 1’s and 2’s
complements,
 Codes-Binary, BCD, Excess 3,Gray, Alphanumeric codes,
Boolean theorems
 Logic gates,
 Universal gates,
 Sum of products and product of sums, Minterms and
Maxterms,
 Karnaugh map minimization,
 NAND and NOR Implementations.

4. Number Systems

5. A set of values used to represent different quantities is known as
number system
Ex: Number of student in online classes
In general term computer represent information in different types
of data forms i.e. number , character ,picture ,audio , video etc
Number Systems

6. Computers are made of a series of switches/ gates.
Each switch has two states: ON(1) or OFF(0).That's why computer works on
the basis of binary number system(0/1).But for different purpose different
number systems are used in computer world to represent information.
E.g. Octal, Decimal, Hexadecimal
Number Systems

7.  This number systems is composed of 10 Symbols
(0,1,2,3,4,5,6,7,8,9)
 the decimal system has 10 numerical characters and so has a
base of 10
Decimal Number System

8.  Binary has only two values 0 and 1
 If larger values than 1 are needed, extra columns are added to
the left. Each column value is now twice the value of the
column to its right. For example the decimal value three is
written 11 in binary
Binary Number System

9. Octal
• Octal has eight values 0 to 7.
• If larger values than 7 are needed, extra columns are added to the
left. Each column value is now 8 times the value of the column to its
right. For example the decimal value twenty-seven is written 33 in
octal
Hexadecimal
• Hexadecimal number system uses base 16 from 0-9 and a,b,c,d,e,f as
16 symbols
Octal and HexaDecimal Number system

10. • 1010 represents the decimal value ten. (1 ten + 0 units)
• 102 represents the binary value two. (1 two + 0 units)
• 108 represents the octal value eight. (1 eight + 0 units)
• 1016 represents the hexadecimal value sixteen. (1 sixteen + 0 units)
Examples

11. Decimal to Any Base
• Decimal to Binary
• Decimal to Octal
• Decimal to Hexadecimal
Any base to Decimal
• Binary to Decimal
• Octal to Decimal
• Hexadecimal to Decimal
Not Involving Decimal
• Binary to Octal
• Octal to Hexa
• Hexa to Binary
Conversions Between Number Systems

12. Decimal to Binary

13. Decimal to Octal

14. Decimal to Hexadecimal

15. Binary to Decimal

16. Octal to Decimal

17. Hexadecimal to Decimal

18. Binary to Octal
To convert a binary number to octal number, these steps are followed
Starting from the least significant bit, make groups of three bits.
If there are one or two bits less in making the groups, 0s can be added after the
most significant bit
Convert each group into its equivalent octal number
101100101012 = 26258
8421
0 1 0
001 100 101 010 011
421421 421 421 421
1 4 5 2 3

19. Binary to Hexadecimal
To convert a binary number to hexadecimal number, these steps are followed −
Starting from the least significant bit, make groups of four bits.
If there are one or two bits less in making the groups, 0s can be added after the
most significant bit.
Convert each group into its equivalent octal number.
1101101101012 = DB516

20. Octal to hexadecimal
Using the below two methods, we can convert the octal number system into the
hexadecimal number system.
1. Convert the octal number into binary and then convert the binary into
hexadecimal.
2. Convert the octal number into decimal and then convert the decimal into
hexadecimal.
Let's convert the octal number into the hexadecimal number system

21. Octal -> Binary -> Hexadecimal
Let's convert (56)8 into hexadecimal
Step 1 : Convert (56)8 into Binary
In order to convert the octal number into binary, we need to express every octal value using 3
binary bits.
Binary equivalent of 5 is (101)2.
Binary equivalent of 6 is (110)2.
= (56)8
= (101)(110)
= (101110)2
Step 2 : Convert (101110)2 into Hexadecimal
In order to convert the binary number into hexadecimal, we need to group every 4 binary bits
and calculate the value[From left to right].
(101110)2 in hexadecimal
= (101110)2
= (10)(1110)
= (2)(14) = = (2E)16

22. (2C1)16 = (1011000001)2
2 C 1
2 12 1
8421 8421 8421
0010 1100 0001
Hex to binary conversion
9DB2)16 = (1001110110110010)2
9 D B 2
9 13 11 2
8421 8421 8421 8421
1001 1101 1011 0010
Every Hexadecimal digits grouping by 4.

23. Decimal to Binary
(10.25)10
Keep multiplying the fractional part with
2 until decimal part 0.00 is obtained.
(0.25)10 = (0.01)2
Example for Fractional part
1010.01

24. Binary to Decimal
(1010.01)2 101101.1001
1x23 + 0x22 + 1x21+ 0x20 + 0x2 -1 + 1x2 -2
= 8+0+2+0+0+0.25 = 10.25
(1010.01)2 = (10.25)10

25. Decimal to Octal
(10.25)10
(10)10 = (12)8 Fractional part: 0.25 x 8 = 2.00
Note: Keep multiplying the fractional part with 8 until decimal part .00 is obtained.
(.25)10 = (.2)8
Answer: (10.25)10 = (12.2)8

26. Octal to Decimal
(12.2)8
1 x 81 + 2 x 80 +2 x 8-1
= 8+2+0.25 = 10.25
(12.2)8 = (10.25)10

27. Arithmetic Operations
Basic Addition and Subtraction
• Binary numbers are added like decimal numbers.
– In decimal, when numbers sum more than 9, a carry results.
– In binary when numbers sum more than 1, a carry takes
place
• Addition is the basic arithmetic operation used by
digital devices for subtraction, multiplication &
division

28. Binary Addition
Addition Rules
0+0= 0
0+1= 1
1+0= 1
1+1= 0 (Sum) with carry 1
1+1+1=1 (Sum) with carry 1

29. Example 1:
9 1 0 0 1
11 1 0 1 1
(1) (1)
20 1 0 1 0 0
Carry
Apply 8421 Code equivalent decimal
Value
8 4 2 1
1 0 0 1
1 0 1 1
1 0 1 0 0
8421 Code
9
11
168421 Code
+

30. Example 2:
10 1 0 1 0
9 1 0 0 1
19 1 0 0 1 1
Apply 8421 Code equivalent
decimal Value
8 4 2 1
1 0 1 0
1 0 0 1
1 0 0 1 1
8421 Code
10
9
168421 Code
+

31. Example 3:
38 1 0 0 1 1 0
53 1 1 0 1 0 1
91 1 0 1 1 0 1 1
+
64 32 16 8 4 2 1
64+16+8+2+1=91

32. 106 1 1 0 1 0 1 0
Example 3:
45 1 0 1 1 0 1
61 1 1 1 1 0 1
+
64 32 16 8 4 2 1
64+16+8+2+1=91
1 1 1 1 Carry

33. Subtraction Rules
0-0= 0
0-1= 1 with Borrow 1
1-0= 1
1-1= 0
Binary Subtraction

34. Example 1:
Subtract (0011)2 from (1100)2
12 1 1 0 0
3 0 0 1 1
9 1 0 0 1
(-)
Borrow
8 4 2 1
8+1=9

35. Example 2:
Subtract (10100)2 from (101101)2
45 1 0 1 1 0 1
20 1 0 1 0 0
25 0 1 1 0 0 1
(-)
32 16 8 4 2 1
16+8+1=25

36. Multiplication Rules
0 x 0= 0
0 x 1= 0
1 x 0= 0
1 x 1= 1
Binary Multiplication

37. Example 1:
(1011)2 Multiplication with (111)2
11 1 0 1 1
7 1 1 1
(x)
64 32 16 8 4 2 1
64+8+4+1=77
1 0 1 1
1 0 1 1
1 0 1 1
Binary
Addition
1 0 0 1 1 0 1
(1)
(1)
(1)
(1)
77

38. Example 2:
(101)2 Multiplication with (11)2
5 1 0 1
3 1 1
(x)
8 4 2 1
8+4+2+1=15
1 0 1 Binary Addition
1 1 1 1
1 0 1
15

39. Example 3:
(110)2 Multiplication with (101)2
6 1 1 0
5 1 0 1
(x)
16 8 4 2 1
16+8+4+2=30
1 1 0
Binary Addition
1 1 1 1 0
0 0 0
30
1 1 0

40. Binary Division
Example 1:
Divide (1001110)2 by (100)2
1 0 0 1 1 1 0
1 0 0
1 0 0
0 0 0 1 1 1
1 0 0
0 1 1 0
1 0 0
0 1 0 0
1 0 0
0 0 0
1 0 0 1 1 . 1
78
4
1 0 0 1 1 . 1
16 8 4 2 1
16+2+1=19
Integer Part Fractional Part
1x2 -1
0.5

41. Binary Division
Example 2:
Divide (1010)2 by (10)2
1 0 1 0
1 0
1 0
0 0 1 0
1 0
0
1 0 1

42. Logic Gates

43.  Identify the basic gates and describe the behavior of
each
 Combine basic gates into circuits
 Describe the behavior of a gate or circuit using
Boolean expressions, truth tables, and logic diagrams
Outline

44. Birth of Logic Gates
Semiconductor
Diode
Transistor Logic Gates

45. Logic Gates
• A logic gate is a device that acts as a building block for digital circuits
• They perform basic logical functions that are fundamental to digital circuits
• Most electronic devices we use today will have some form of logic gates in them
• For example, logic gates can be used in technologies such as smartphones, tablets
or within memory devices
• In a circuit, logic gates will make decisions based on a combination of digital
signals coming from its inputs. Most logic gates have two inputs and one output
• At any given moment, every terminal is in one of the
two binary conditions, false or true. False represents 0, and true represents 1
• Logic gates are commonly used in integrated circuits (IC)

46. AND
OR
NOT
Basic Gates
NAND
NOR
Universal Gates
X OR
XNOR
Special Gates
Logic Gates

47. How do we describe the behavior of gates and circuits?
Boolean expressions
Uses Boolean algebra, a mathematical notation for expressing two-
valued logic
Logic diagrams
A graphical representation of a circuit; each gate has its
own symbol
Truth tables
A table showing all possible input value and the associated
output values

48. AND Gate
A
B
Q
A B Q
0 0 0
0 1 0
1 0
1 1 1
0
Truth Table
Q=A.B
Boolean expressions

49. A
B
Q
A B Q
0 0 0
0 1 1
1 0 1
1 1 1
OR Gate Truth Table
Q=A+B
Boolean expressions

50. A Q
A Q
0 1
1 0
NOT Gate Truth Table
Q=A
Boolean expressions

51. A
B
C
Q
NAND Gate

52. A
B
C
Q
A B C Q
0 0 0
0 1 0
1 0 0
1 1 1
1
1
1
0
Q = NOT (AAND B)
AND and NOT Gate (NAND)
Truth Table
Q=A.B
Boolean expressions

53. NOR Gate
A
B
C

54. A
B
Q
C
A B C Q
0 0 0
0 1 1
1 0 1
1 1 1
1
0
0
0
OR and NOT Gate (NOR)
Truth Table
Q=A+B
Boolean expressions

55. A
B
XOR Gate
C=A B
+

56. A B C
0 0 0
0 1 1
1 0 1
1 1 0
XOR Gate

57. A
B
XNOR Gate
C=A B
+

58. A B C
0 0 1
0 1 0
1 0 0
1 1 1
XNOR Gate

59. OR
A
Y
NOT
AND
B
C
AND
2# of Inputs = # of Combinations
2 3 = 8
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
A B C
Combinational Circuits
Y

60. OR
A
Y
NOT
AND
B
C
AND
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
A B C
0
0
0
0
1
0
0
0
Y

61. 0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
A B C
0
OR
A
Y
NOT
AND
B
C
AND
0
0
1
0
1
1
1
1
Y

62. 0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
A B C
0
1
0
OR
A
Y
NOT
AND
B
C
AND
0
1
0
0
1
0
0
0
Y

63. 0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
A B C
0
1
0
0
OR
A
Y
NOT
AND
B
C
AND
0
1
1
0
1
1
1
1
Y

64. 0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
A B C
0
1
0
1
0
0
1
0
OR
A
Y
NOT
AND
B
C
AND
1
1
1
1
0
0
1
1
Y

65. 65
Gates are combined into circuits by using the output of
one gate as the input for another
Combinational Circuits

66. 66
 Three inputs require eight rows to describe all possible input
combinations
 This same circuit using a Boolean expression is (AB + AC)
Combinational Circuits

67. 67
Consider the following Boolean expression A(B + C)
Does this truth table look familiar?
Combinational Circuits

68. 68
Combinational Circuits
Circuit equivalence
 Two circuits that produce the same output for
identical input
 Boolean algebra allows us to apply provable
mathematical principles to help design circuits
 A(B + C) = AB + BC (distributive law) so circuits
must be equivalent

69. 1’s and 2’s Complement
1’s Complement
• 1’s complement of N is defined as (2n -1)-N.
– If n=4 have (2n -1) being 1 0000 - 1 = 1111
• So for n=4 would subtract any 4-bit binary number
from 1111.
• This is just inverting each bit.
• Example: 1’s compliment of 1011001
• is 0100110

70. 2’s complement
• The 2’s complement is defined as 2n-N
• Can be done by subtraction of N from 2n or
adding 1 to the 1’s complement of a number.
• For 6 = 0110
– The 1’s complement is 1001
+1
– The 2’s complement is 1010

71. Codes
Reflection Code Sequential Code
Alphanumeric
Codes
Error Detection
and Correction
Codes
Weighted Code
Non Weighted
Code
Codes
-Group of Symbols
Binary,
8421,
2421
Excess
3, Gray
Self
Complement
Code, xs 3
XS3,
8421
ASCII
Hamming
Code

72. Binary Codes
“An n-bit binary code is a group of n bits that
assume up to 2n distinct combinations of 1s
and 0s, with each combination representing
one element of the set being coded”

73. Binary Coded Decimal (BCD)
• The BCD is simply the 4 bit representation of
the decimal digit.
• It’s a Positioned Weight
11

74. 16 8 4 2 1
12 => 1 1 0 0 (Binary form)
Example for BCD
0001 0010
1 2
Decimal
BCD 10010

75. Excess 3 Code
Excess of 3 to the BCD
For an Example we take Decimal 22
2 2 0010 0010
Decimal BCD
3 3
5 5
0011 0011 Excess of 3 added with BCD
0101 0101 Excess 3 Code for 22

76. Alphanumeric Codes
• Alphanumeric codes, also called character codes, are
binary codes used to represent alphanumeric data
• ASCII

77. Gray Code
• Its known as Reflected Codes
• Unweighted Codes
• We call it Gray Code after Frank Gray
• Unit Distance Code and Minimum Error Code
• Cyclic Code

78. • Two Successive Values differ in
only 1 Bit
• Binary number is converted to Gray
Code to reduce switching
Operations
• Widely Used in Error Correction in
Digital Communications
Decimal Binary Gray

79. Binary to Gray Code
0000 0000
Decimal Binary Gray
+ +
+
0001 0001
+ +
+
X OR Operation
0
1
Decimal Binary Gray

80. Boolean Algebra
• VERY nice machinery used to manipulate (simplify) Boolean
functions
• George Boole (1815-1864): “An investigation of the laws of
thought”
• Terminology:
– Literal: A variable or its complement
– Product term: literals connected by •
– Sum term: literals connected by +

81. Boolean Algebra Properties
Let X: boolean variable, 0,1: constants
1. X + 0 = X -- Zero Axiom
2. X • 1 = X -- Unit Axiom
3. X + 1 = 1 -- Unit Property
4. X • 0 = 0 -- Zero Property

82. Let X: boolean variable, 0,1: constants
5. X + X = X -- Idepotence
6. X • X = X -- Idepotence
7. X + X’ = 1 -- Complement
8. X • X’ = 0 -- Complement
9. (X’)’ = X -- Involution

83. Let X,Y, and Z: boolean variables
10. X + Y = Y + X 11. X • Y = Y • X -- Commutative
12. X + (Y+Z) = (X+Y) + Z 13. X•(Y•Z) = (X•Y)•Z -- Associative
14. X•(Y+Z) = X•Y + X•Z 15. X+(Y•Z) = (X+Y) • (X+Z) -- Distributive
16. (X + Y)’ = X’ • Y’ 17. (X • Y)’ = X’ + Y’ -- DeMorgan’s
In general,
( X1 + X2 + … + Xn )’ = X1’•X2’• … •Xn’, and
( X1•X2•… •Xn )’ = X1’ + X2’ + … + Xn’

100. K Map Simplifications
What are Karnaugh maps?
• Karnaugh maps provide an alternative way of simplifying logic circuits.
• Instead of using Boolean algebra simplification techniques, you can transfer
logic values from a Boolean statement or a truth table into a Karnaugh map.
• The arrangement of 0's and 1's within the map helps you to visualise the
logic relationships between the variables and leads directly to a simplified
Boolean statement.

101. • Karnaugh maps, or K-maps, are often used to simplify logic problems with 2,
3 or 4 variables.
Cell = 2n ,where n is a number of variables

109. Expression is A

111. A+B

113. 3 Variables K Map

114. A B
A+B

116. 4 Variable K Map

117. A.B + C’.D

132. Thank you