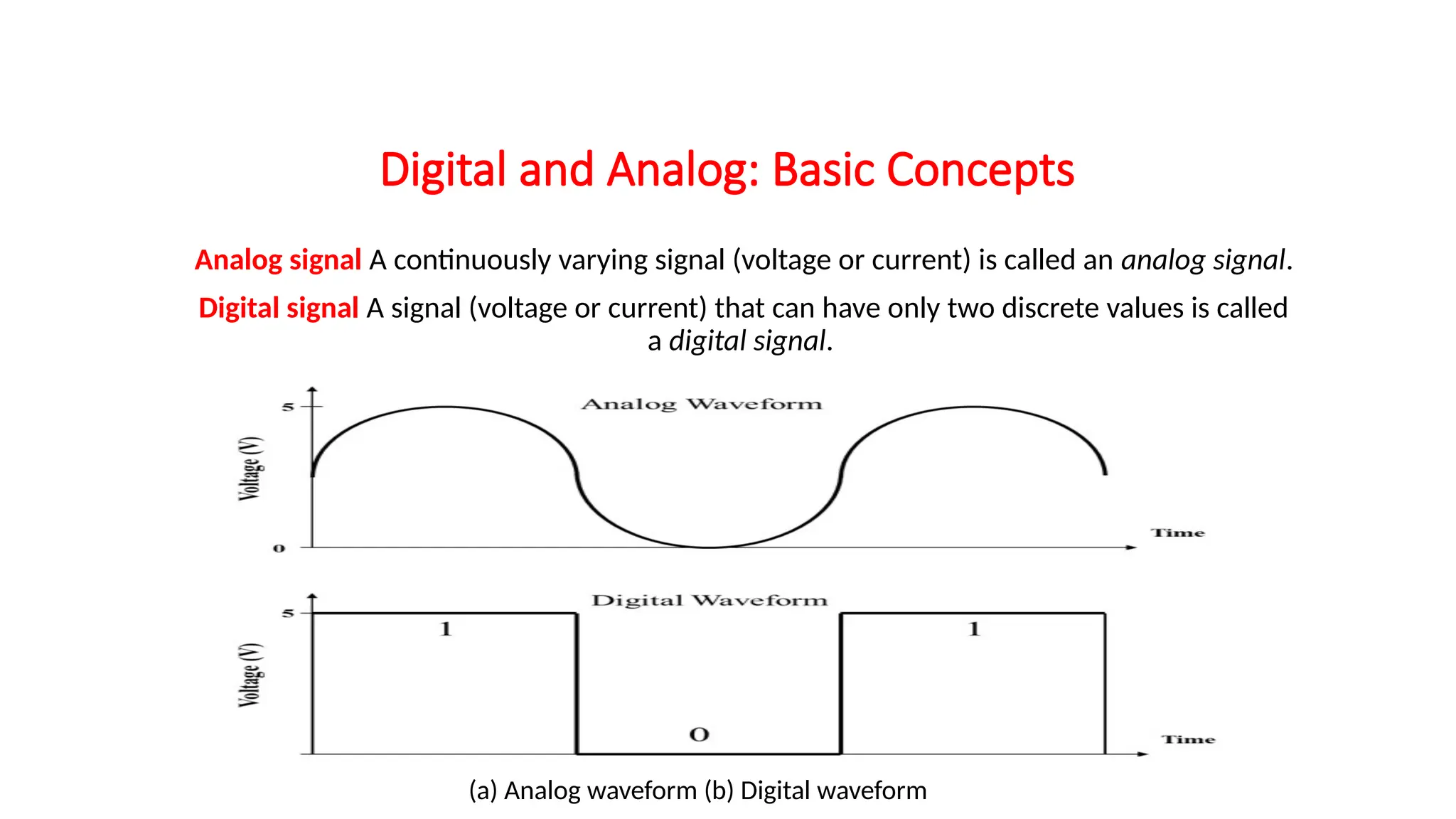
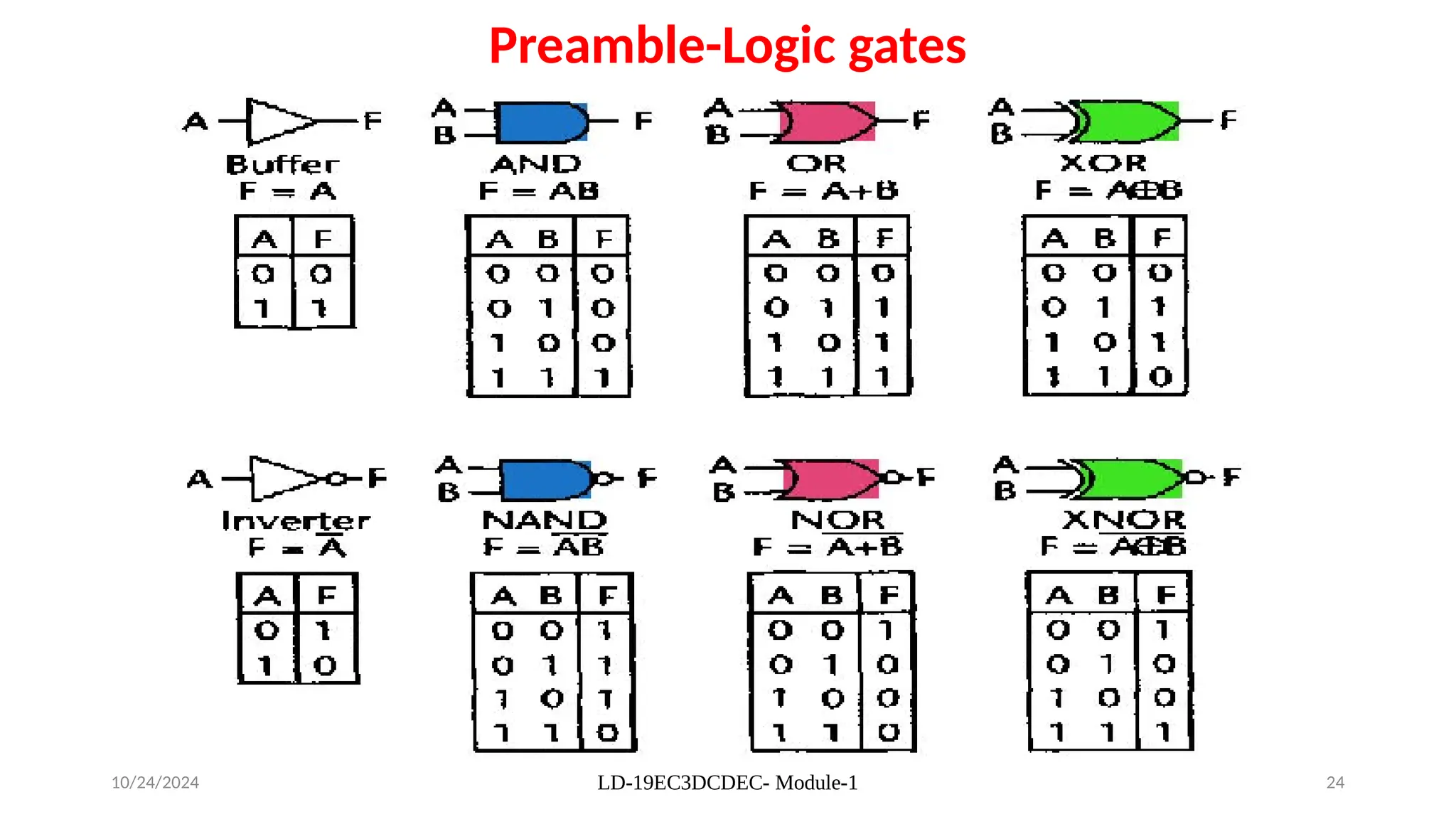
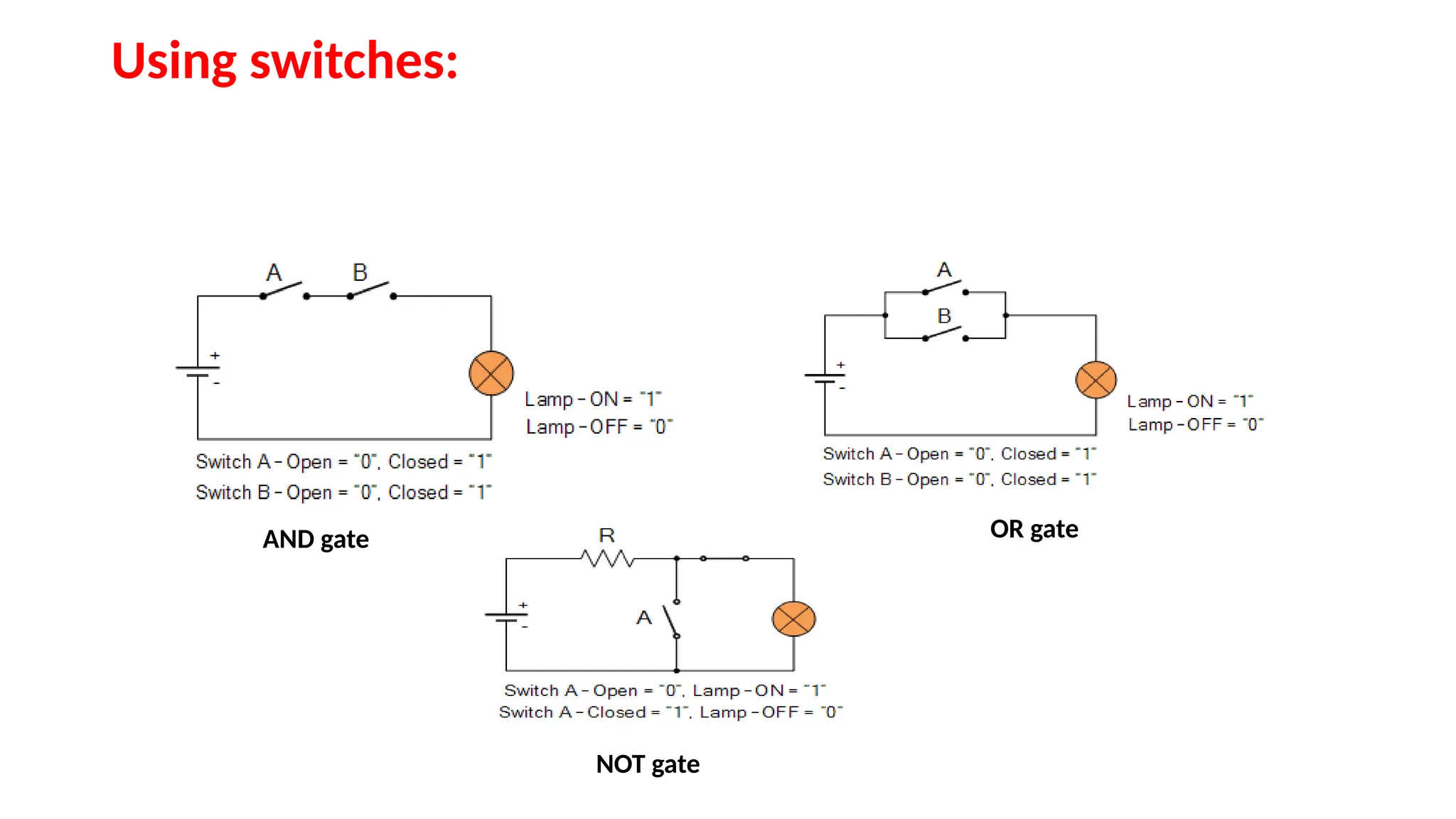
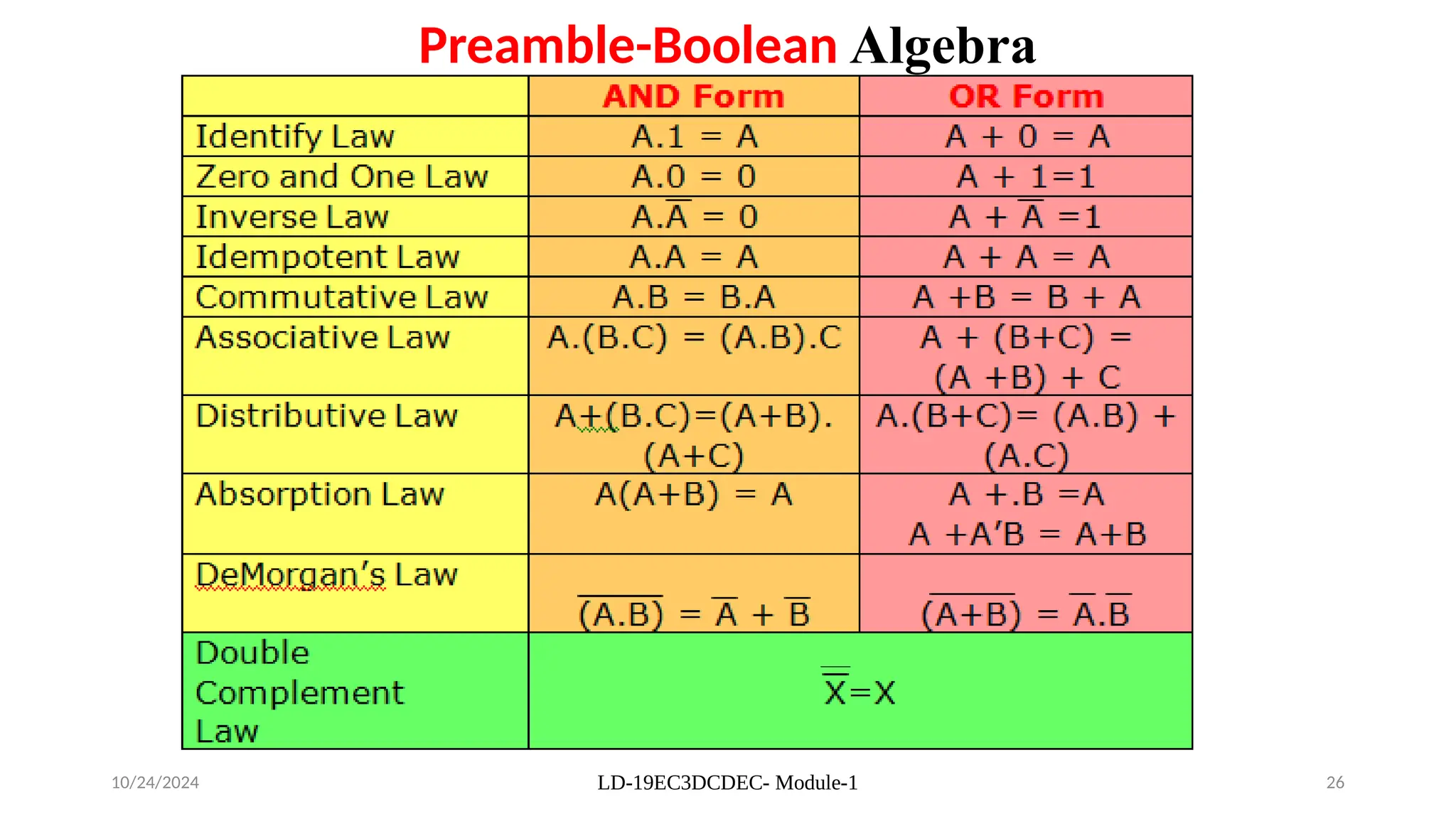
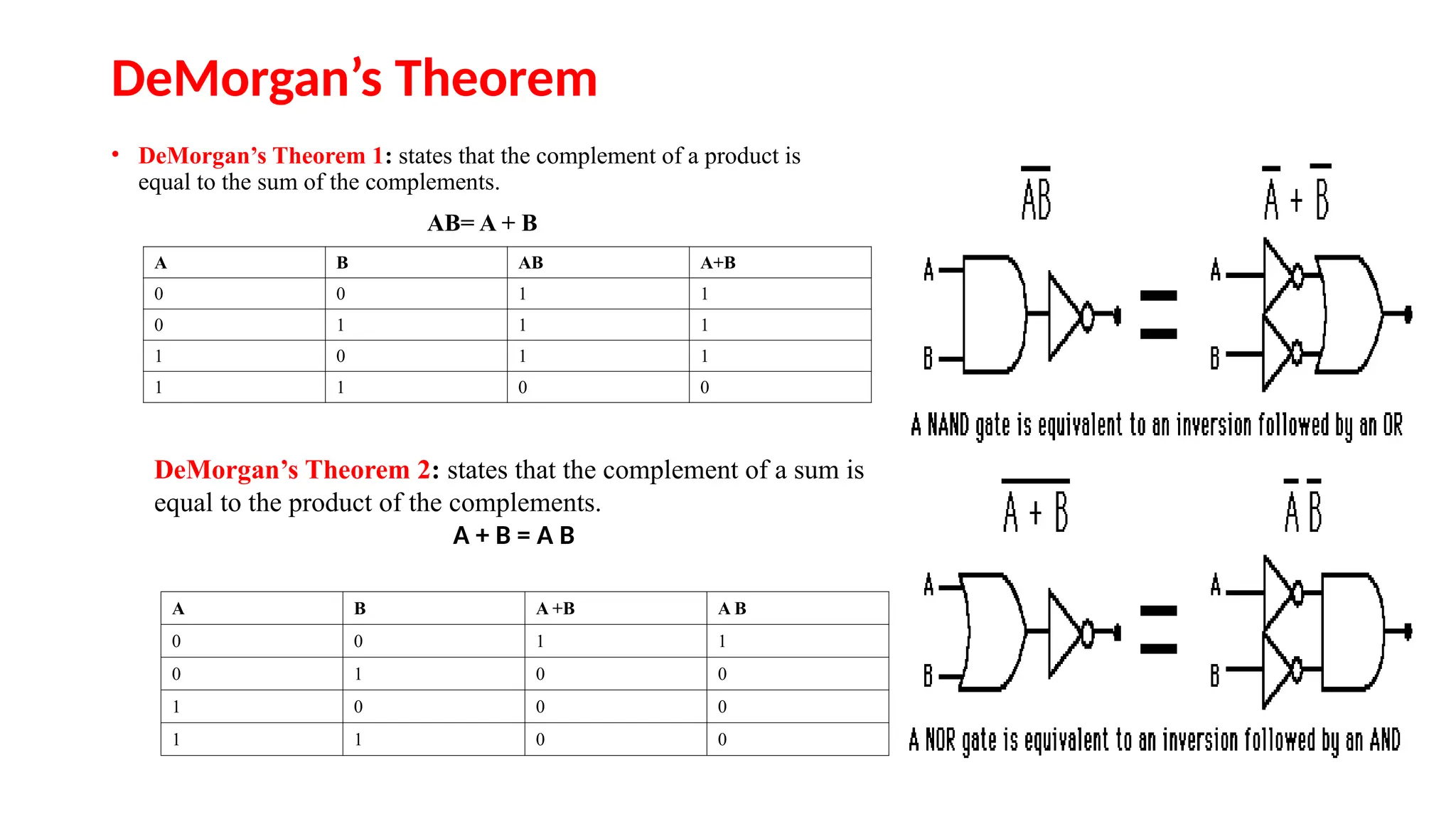
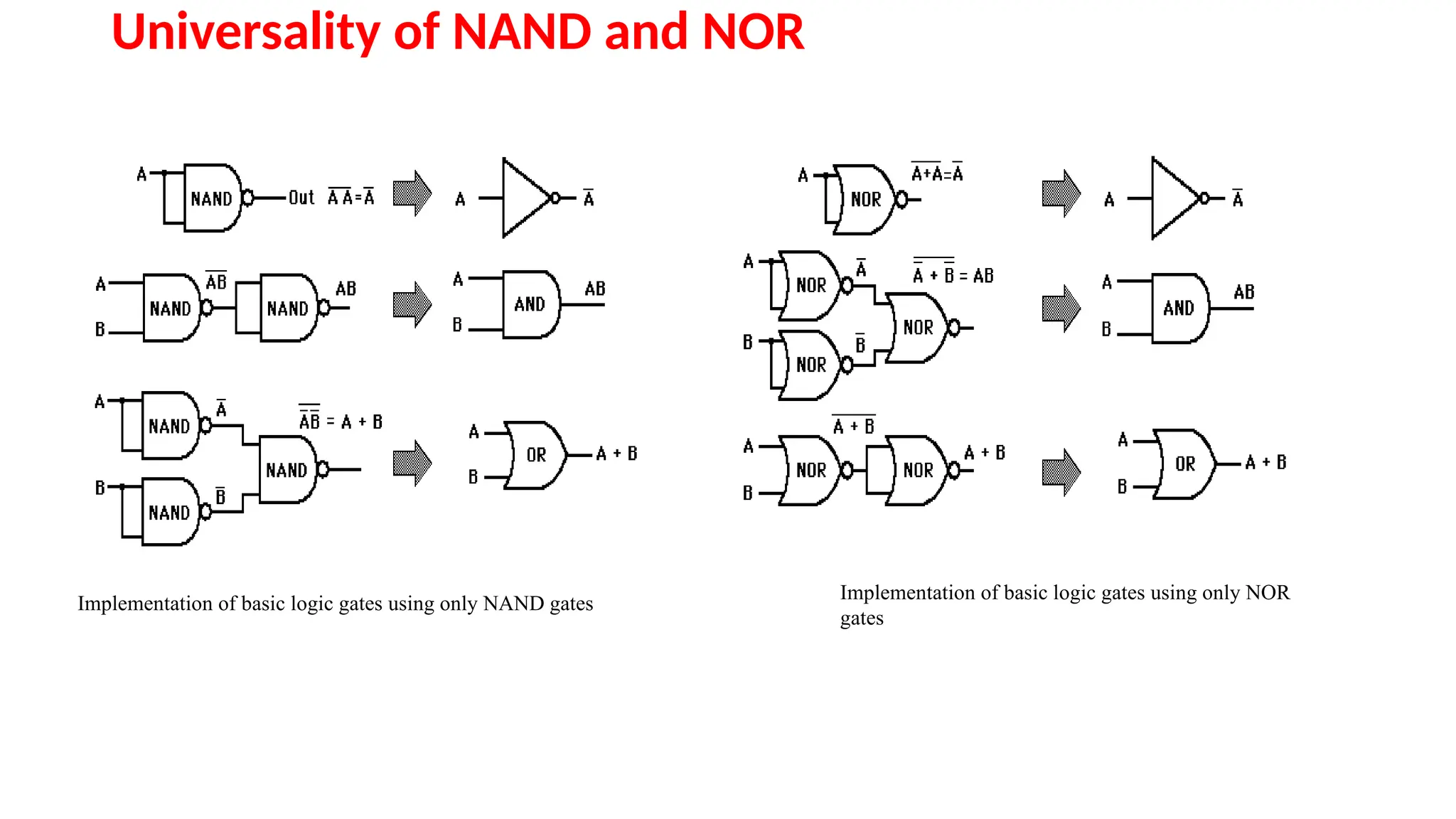
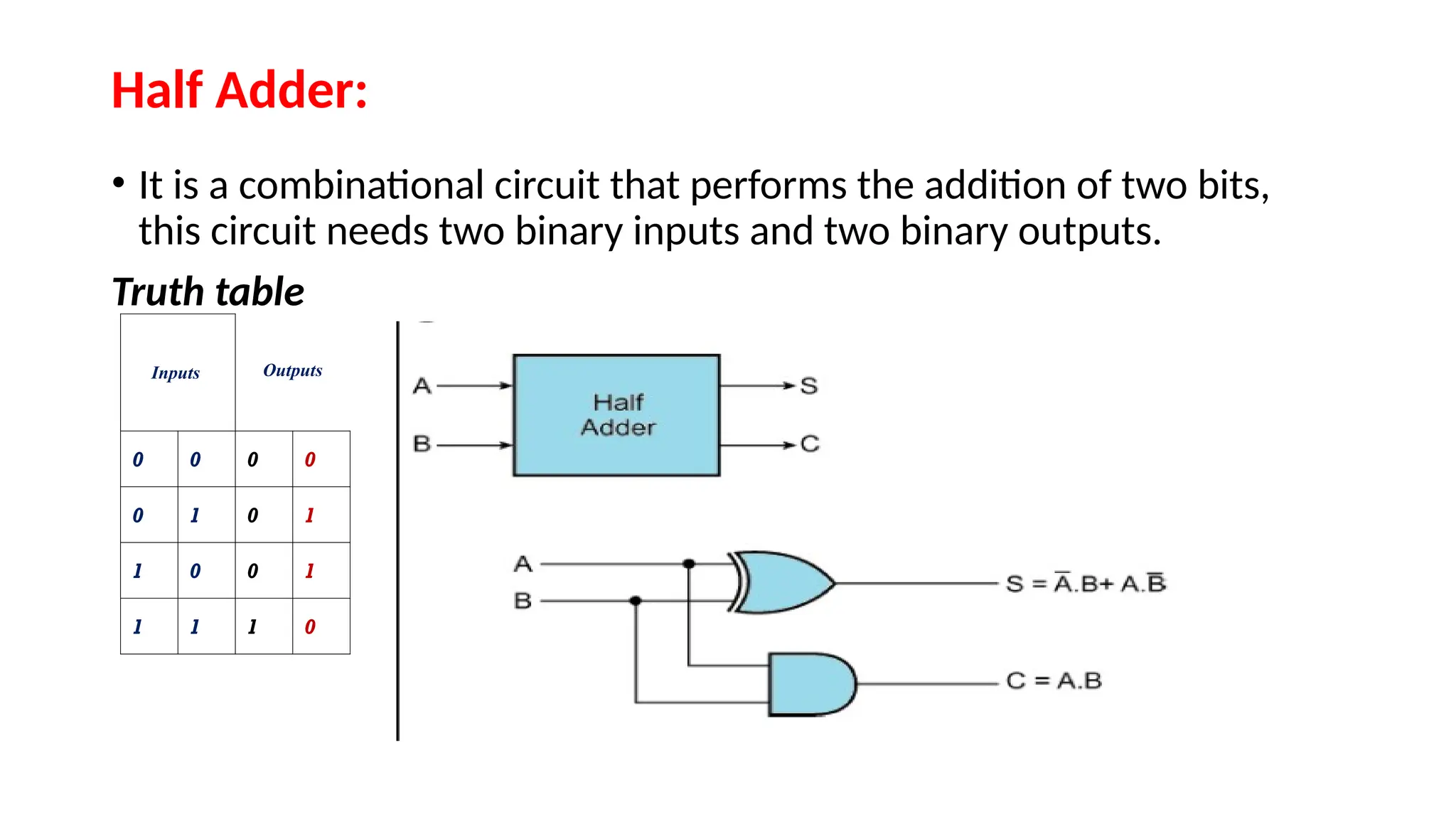
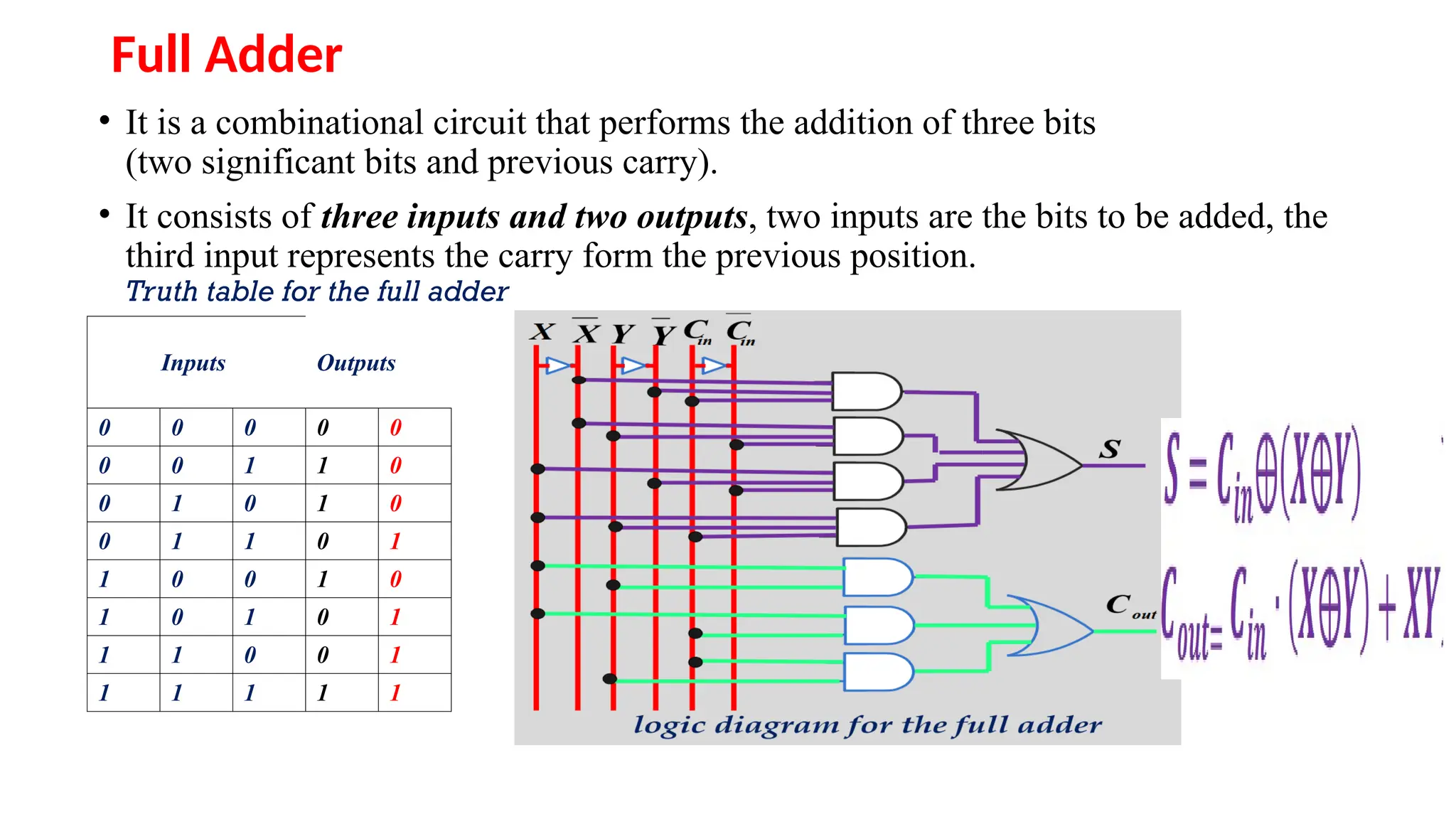
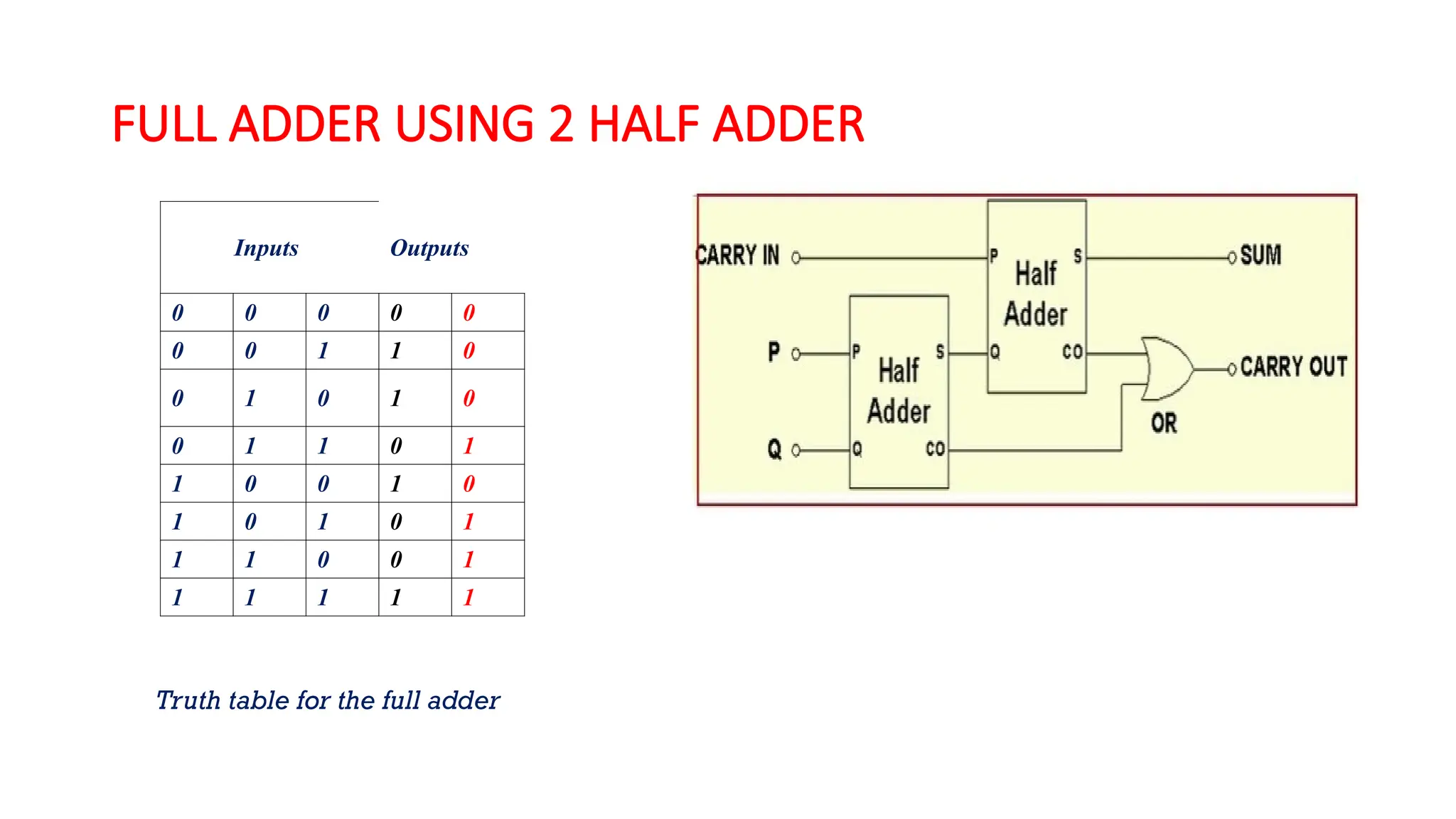
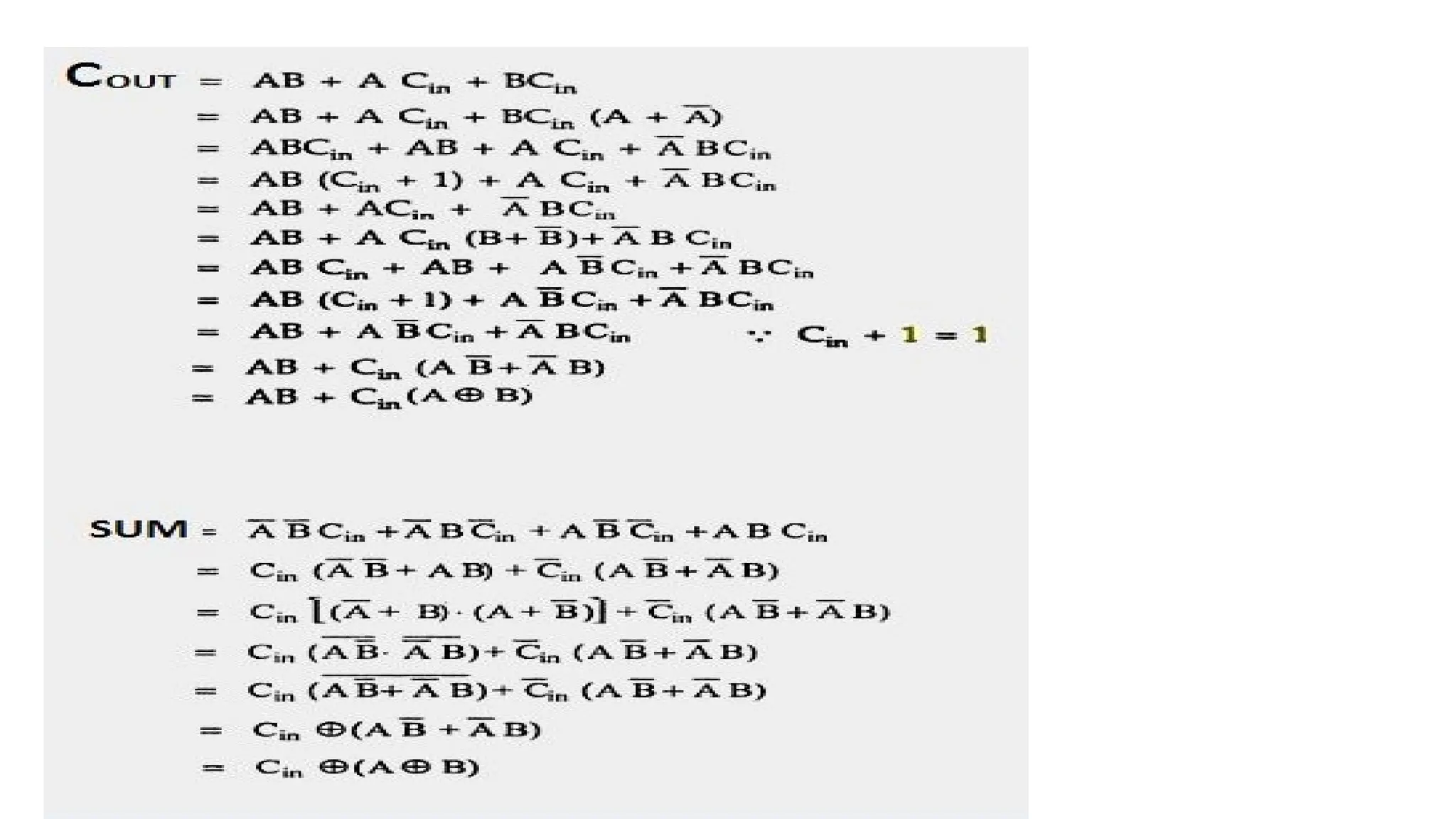The document provides an overview of digital electronics, focusing on number systems such as binary, decimal, octal, and hexadecimal, alongside their conversions. It discusses basic concepts of digital and analog signals, boolean algebra, and logic gates, including the implementation of half and full adders. Additionally, it covers the arithmetic methods of 1's and 2's complements, along with De Morgan's theorem for boolean functions.

1. DEPARTMENT
OF
ELECTRONICS & COMMUNICATION ENGINEERING
BASIC ELECTRONICS
MODULE-1 Digital Electronics
BY
Prof M SHRUTHI

2.  Module – 1 Contents
 Digital Electronics 1
• Introduction to Number Systems
• Binary Number System
• Decimal Number System
• Octal Number System
• Hexadecimal Number System
• Conversion from one number system to another number system
• 1’s and 2’s complement method and their arithmetic
 Digital Electronics 2
• Binary logic functions
• Boolean algebra
• De-Morgan’s Theorem
• Logic gates
• Realization of Boolean functions using basic gates
• Implementation of logic gates as half & full adder

3. Digital and Analog: Basic Concepts
Analog signal A continuously varying signal (voltage or current) is called an analog signal.
Digital signal A signal (voltage or current) that can have only two discrete values is called
a digital signal.
(a) Analog waveform (b) Digital waveform

4. 4
• Number systems include decimal, binary, octal and
hexadecimal
• Each system have four number base
Number System Base Symbol
Binary Base 2 B
Octal Base 8 O
Decimal Base 10 D
Hexadecimal Base 16 H

5. 5
Base-N Number System
• Base N
• N Digits: 0, 1, 2, 3, 4, 5, …, N-1
• Example: 1045N
• Positional Number System
•
• Digit do is the least significant digit (LSD).
• Digit dn-1 is the most significant digit (MSD).
1 4 3 2 1 0
1 4 3 2 1 0
n
n
N N N N N N
d d d d d d





6. 6
Decimal Number System
• Base 10
• Ten Digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
• Example: 104510
• Positional Number System
• Digit d0 is the least significant digit (LSD).
• Digit dn-1 is the most significant digit (MSD).
1 4 3 2 1 0
1 4 3 2 1 0
10 10 10 10 1010
n
n
d d d d d d





7. 7
Binary Number System
• Base 2
• Two Digits: 0, 1
• Example: 10101102
• Positional Number System
• Binary Digits are called Bits
• Bit bo is the least significant bit (LSB).
• Bit bn-1 is the most significant bit (MSB).
1 4 3 2 1 0
1 4 3 2 1 0
2 2 2 2 2 2
n
n
b b b b b b





8. 8
Octal System
• Computer scientists are often looking for shortcuts
to do things
• One of the ways in which we can represent binary
numbers is to use their octal equivalents instead
• This is especially helpful when we have to do fairly
complicated tasks using numbers
• The octal numbering system includes eight base
digits (0-7)
• After 7, the next placeholder to the right begins with
a “1”
• 0, 1, 2, 3, 4, 5, 6, 7, 10, 11, 12, 13 ...

9. 9
Decimal Number System
• The Decimal Number System uses base 10. It includes
the digits {0, 1,2,…, 9}. The weighted values for each
position are:
10^4 10^3 10^2 10^1 10^0 10^-1 10^-2 10^-3
10000 1000 100 10 1 0.1 0.01 0.001
Base
Right of decimal point
left of the decimal point

10. 10
Converting Base-2 to Base-10
(1 0 1 1)2
0
ON
OFF
ON
ON/OFF
OFF
ON
Exponent: 20
21
22
23
24
Calculation: 0 0 2 1
16+ + + + =
(19)10

11. Hexadecimal system

12. 12
• Each digit appearing to the left of the decimal point represents a value
between zero and nine times power of ten represented by its position in
the number.
• Digits appearing to the right of the decimal point represent a value
between zero and nine times an increasing negative power of ten.
• Example: the value 725.194 is represented in expansion form as follows:
• 7 * 10^2 + 2 * 10^1 + 5 * 10^0 + 1 * 10^-1 + 9 * 10^-2 + 4 * 10^-3
• =7 * 100 + 2 * 10 + 5 * 1 + 1 * 0.1 + 9 * 0.01 + 4 * 0.001
• =700 + 20 + 5 + 0.1 + 0.09 + 0.004
• =725.194

13. 13
The Binary Number Base Systems
• Most modern computer system using binary logic. The
computer represents values(0,1) using two voltage levels
(usually 0V for logic 0 and either +3.3 V or +5V for logic 1).
• The Binary Number System uses base 2 includes only the
digits 0 and 1
• The weighted values for each position are :
2^5 2^4 2^3 2^2 2^1 2^0 2^-1 2^-2
32 16 8 4 2 1 0.5 0.25
Base

14. 14
Number Base Conversion
• Binary to Decimal: multiply each digit by its weighted
position, and add each of the weighted values together
or use expansion formdirectly.
• Example: the binary value 1100 1010 represents :
• 1*2^7 + 1*2^6 + 0*2^5 + 0*2^4 + 1*2^3 + 0*2^2 +
1*2^1 + 0*2^0
• =1 * 128 + 1 * 64 + 0 * 32 + 0 * 16 + 1 * 8 + 0 * 4 + 1 *
2 + 0 * 1
• =128 + 64 + 0 + 0 + 8 + 0 + 2 + 0 =
• =202

15. Binary → hex/decimal/octal conversion
• Conversion from binary to octal/hex
• Binary: 10011110001
• Octal: 10 | 011 | 110 | 001=23618
• Hex: 100 | 1111 | 0001=4F116
• Conversion from binary to decimal
• 1012= 1×22
+ 0×21
+ 1×20
= 510
• 63.48 = 6×81
+ 3×80
+ 4×8–1
= 51.510
• A116= 10×161
+ 1×160
= 16110

16. Decimal→ binary/octal/hex conversion
• Why does this work?
• N=5610=1110002
• Q=N/2=56/2=111000/2=11100 remainder 0
• Each successive divide liberates an LSB (least
significant bit)

17. The basics: Binary numbers
• Bases we will use
• Binary: Base 2
• Octal: Base 8
• Decimal: Base 10
• Hexadecimal: Base 16
• Positional number system
• 1012= 1×22
+ 0×21
+ 1×20
• 638 = 6×81
+ 3×80
• A116= 10×161
+ 1×160
• Addition and subtraction
1011
+ 1010
10101
1011
– 0110
0101

18. Sign-and-magnitude
• The most-significant bit (MSB) is the sign digit
• 0 ≡ positive
• 1 ≡ negative
• The remaining bits are the number’s magnitude
• Problem 1: Two representations for zero
• 0 = 0000 and also –0 = 1000
• Problem 2: Arithmetic is cumbersome

19. Ones-complement

20. Ones-complement
• Negative number: Bitwise complement positive number
• 0011 ≡ 310
• 1100 ≡ –310
• Solves the arithmetic problem
• Remaining problem: Two representations for zero
• 0 = 0000 and also –0 = 1111

21. Twos-complement

22. Twos-complement
• Negative number: Bitwise complement plus
one
• 0011 ≡ 310
• 1101 ≡ –310
• Number wheel
0000
0001
0011
1111
1110
1100
1011
1010
1000 0111
0110
0100
0010
0101
1001
1101
0
+ 1
+ 2
+ 3
+ 4
+ 5
+ 6
+ 7
– 8
– 7
– 6
– 5
– 4
– 3
– 2
– 1
 Only one zero!
 MSB is the sign
digit
 0 ≡ positive
 1 ≡ negative

23. Twos-complement (con’t)
• Complementing a complement  the original
number
• Arithmetic is easy
• Subtraction = negation and addition
• Easy to implement in hardware

24. 10/24/2024 LD-19EC3DCDEC- Module-1 24
Preamble-Logic gates

25. Using switches:
AND gate OR gate
NOT gate

26. 10/24/2024 LD-19EC3DCDEC- Module-1 26
Preamble-Boolean Algebra

27. DeMorgan’s Theorem
• DeMorgan’s Theorem 1: states that the complement of a product is
equal to the sum of the complements.
AB= A + B
A B AB A+B
0 0 1 1
0 1 1 1
1 0 1 1
1 1 0 0
DeMorgan’s Theorem 2: states that the complement of a sum is
equal to the product of the complements.
A + B = A B
A B A +B A B
0 0 1 1
0 1 0 0
1 0 0 0
1 1 0 0

28. Universality of NAND and NOR
Implementation of basic logic gates using only NOR
gates
Implementation of basic logic gates using only NAND gates

29. Half Adder:
• It is a combinational circuit that performs the addition of two bits,
this circuit needs two binary inputs and two binary outputs.
Truth table
Inputs Outputs
0 0 0 0
0 1 0 1
1 0 0 1
1 1 1 0

30. Full Adder
• It is a combinational circuit that performs the addition of three bits
(two significant bits and previous carry).
• It consists of three inputs and two outputs, two inputs are the bits to be added, the
third input represents the carry form the previous position.
Truth table for the full adder
Inputs Outputs
0 0 0 0 0
0 0 1 1 0
0 1 0 1 0
0 1 1 0 1
1 0 0 1 0
1 0 1 0 1
1 1 0 0 1
1 1 1 1 1

31. FULL ADDER USING 2 HALF ADDER
Inputs Outputs
0 0 0 0 0
0 0 1 1 0
0 1 0 1 0
0 1 1 0 1
1 0 0 1 0
1 0 1 0 1
1 1 0 0 1
1 1 1 1 1
Truth table for the full adder