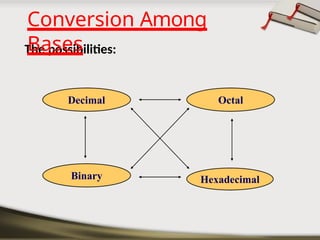
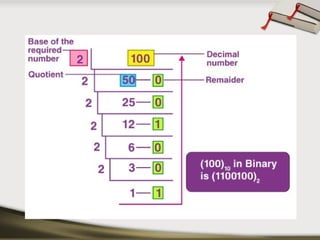
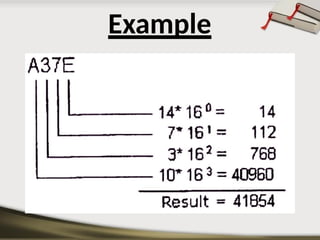
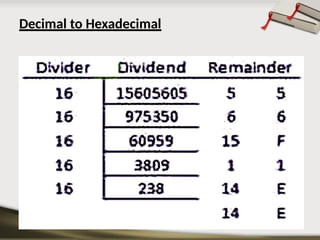
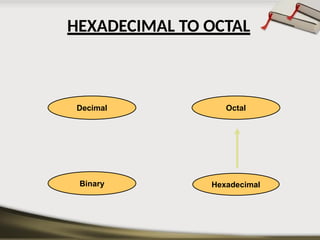
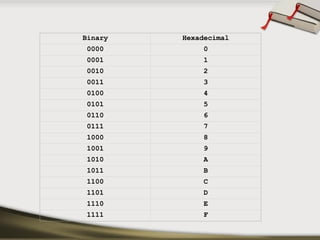
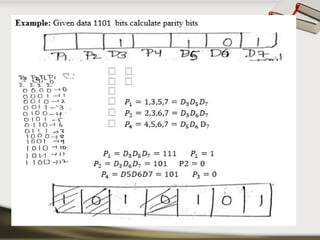
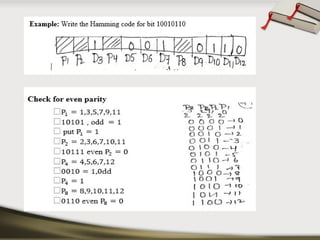
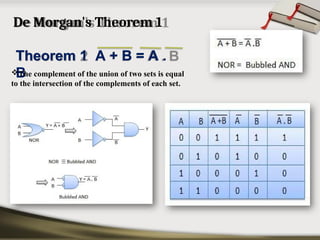
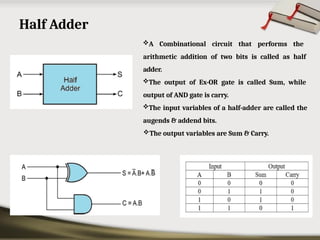
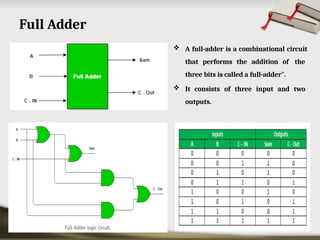
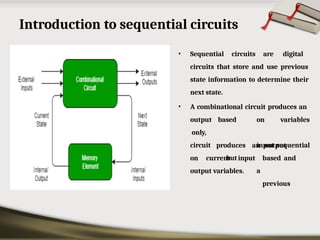
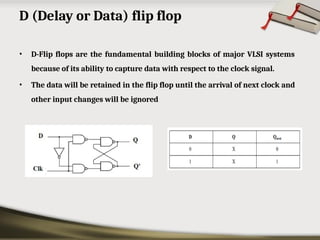
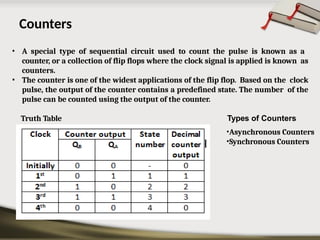
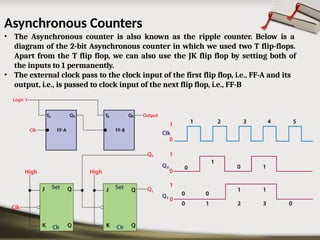
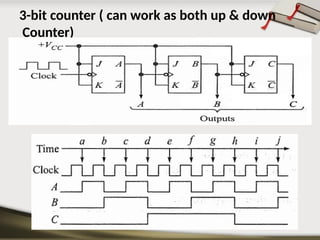
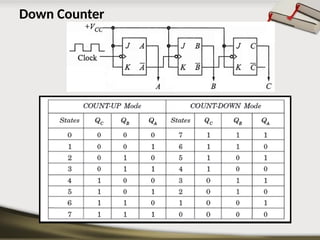
The document provides an overview of various number systems used in digital electronics, including binary, decimal, octal, and hexadecimal systems. It discusses conversion techniques between these systems, encoding methods like Binary Coded Decimal (BCD) and Gray code, and introduces basic logic gates and their functions. Additionally, it covers combinational circuits, sequential circuits, and the types of flip-flops used in electronic systems.
![Basic Electrical and Electronics Engineering
Part – B
Unit 3 – Digital Electronics
By
Dr.S.A.Sivakumar [Dean-Academics, ASKW]
Mr.B.Naga Rajesh(Ph.D) [AP-ECE, ASKW]](https://image.slidesharecdn.com/beee-partb-unit3ppt-241105035714-7d0571db/85/BEEE-Part-B-Unit-3-Digital-Electronics-PPT-pptx-1-320.jpg)