Download as PDF, PPTX
Uploaded byDaria Bogdanova
Applied statistics lecture_2
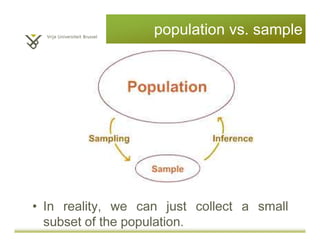
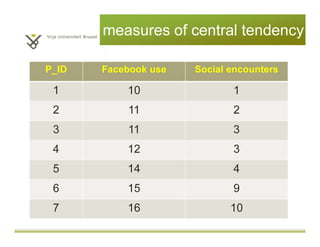
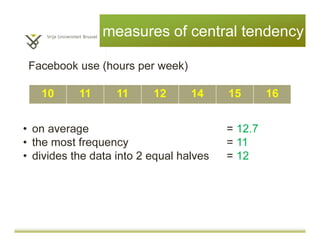
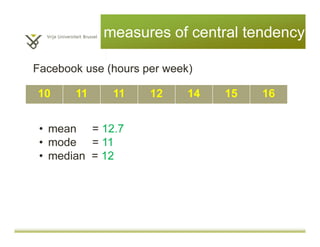
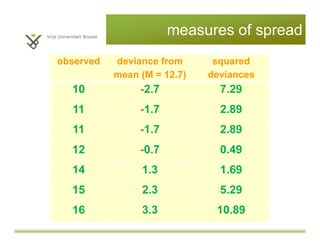
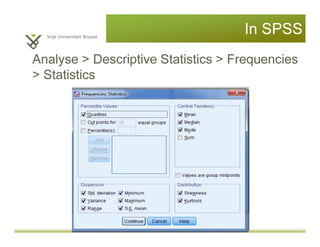
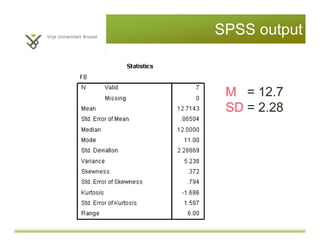
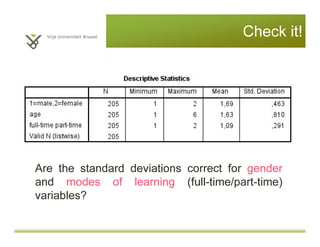
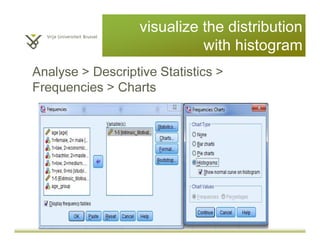
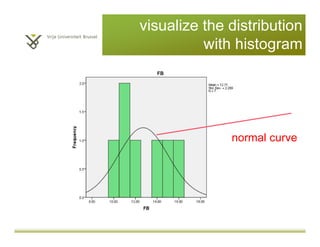
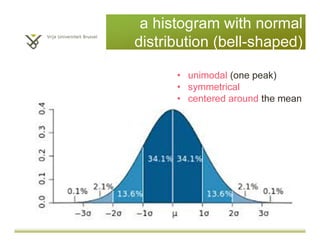
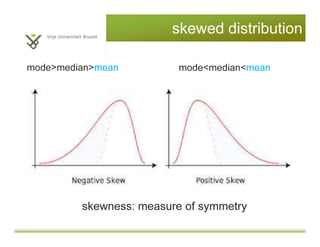
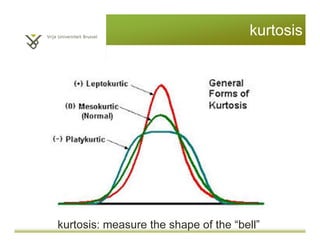
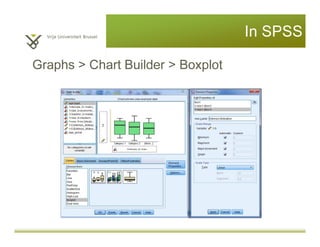
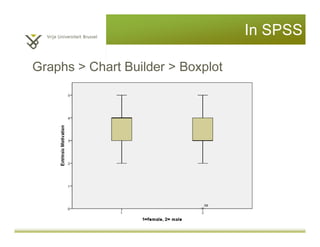
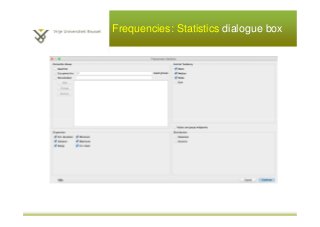
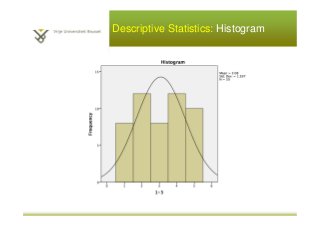
This document provides an introduction to descriptive statistics and statistical methods. It discusses the aims of exploring data through descriptive statistics like measures of central tendency (mean, median, mode) and dispersion (range, variance, standard deviation). It also covers testing assumptions like normal distribution through histograms and statistical tests. Examples are provided to demonstrate calculating and interpreting these descriptive statistics in SPSS. Practices are included to have the reader conduct descriptive analyses and normality tests on sample data sets in SPSS.
More Related Content
Similar to Applied statistics lecture_2
Applied statistics lecture_2
- 1. Introduction to appliedstatistics & applied statistical methods Prof. Dr. Chang Zhu1
- 2. Aims • Exploring data(descriptive statistics) central tendency data distribution (spread/dispersion) • Testing assumption normal distribution
- 3. population vs. sample •In reality, we can just collect a small subset of the population.
- 4. descriptive vs. inferential •Inferential statistics: draw conclusions based on a data set (sample) to the entire population. • Descriptive statistics: summarize a data set
- 5. descriptive statistics • Measuresof central tendency (mean, median, mode) • Measures of spread or dispersion (range, variance, standard deviation)
- 6. measures of centraltendency • A researcher is interested in the degree to which a person spends time on Facebook (in hours per week) and the amount of time spent socialising with friends (number of social encounters per month). • He comes up with the following data set. (adapted from http://wps.pearsoned.co.uk/ema_uk_he_dancey_statsmath _4/84/21626/5536329.cw/index.html)
- 7. measures of centraltendency P_ID Facebook use Social encounters 1 10 1 2 11 2 3 11 3 4 12 3 5 14 4 6 15 9 7 16 10
- 8. measures of centraltendency 10 11 11 12 14 15 16 Facebook use (hours per week) • How many hours do the participants spend on average? (sum = 89) • What is the score that occurs with the most frequency? • What is the score that divides the data into 2 equal halves?
- 9. measures of centraltendency 10 11 11 12 14 15 16 Facebook use (hours per week) • Mean: on average = 12.7 • Mode: the most frequency = 11 • Medium: divides the data into 2 equal halves = 12
- 10. measures of centraltendency 10 11 11 12 14 15 16 Facebook use (hours per week) • mean = 12.7 • mode = 11 • median = 12
- 11. measures of centraltendency – Mean: For normally distributed data, measured as interval and ratio (scales), the appropriate measure of central tendency is the mean. – Median: The median is most appropriate for data measured as ordinal (but can still be used for continuous data) – Mode: is the appropriate measure of central tendency for nominal data.
- 12. measures of spread observeddeviance from mean (M = 12.7) squared deviances 10 -2.7 7.29 11 -1.7 2.89 11 -1.7 2.89 12 -0.7 0.49 14 1.3 1.69 15 2.3 5.29 16 3.3 10.89
- 13. measures of spread Howrepresentative is the mean? • add up all the squared deviances: sum of squared errors affected by sample size • divide by the number of participants minus 1: variance • square root the variance: standard deviation
- 14. measures of spread •Range: the difference between the highest (maximum) and lowest (minimum) scores. e.g. range = 16-10 = 6 not quite objective, depending on the length of the data set.
- 15. In SPSS Analyse >Descriptive Statistics > Frequencies > Statistics
- 16. SPSS output M =12.7 SD = 2.28
- 17. Check it! Are thestandard deviations correct for gender and modes of learning (full-time/part-time) variables?
- 18. visualize the distribution withhistogram Analyse > Descriptive Statistics > Frequencies > Charts
- 19. normal curve visualize thedistribution with histogram
- 20. a histogram withnormal distribution (bell-shaped) • unimodal (one peak) • symmetrical • centered around the mean
- 21.
- 22. kurtosis kurtosis: measure theshape of the “bell”
- 23. testing assumption quantifying normaldistribution: • the Kolmogorov-Smirnov (K-S) test and the Shapiro-Wilk test: compare the scores of our data set with a normally distributed set of scores with the same mean and standard deviation) • p>.05: non-significant not different: normally distributed • p<.05: significant different : non-normal
- 24. normality assumption • notnormally distributed • outliers: a score which is very different from the others • How to identify outliers? Boxplot
- 25. In SPSS Graphs >Chart Builder > Boxplot
- 26. In SPSS Graphs >Chart Builder > Boxplot
- 27. Questions? • Descriptive statistics(mean, median, mode, range, variance, standard deviation) • Skewness/Kurtosis • Histogram to visualize the distribution In SPSS: Analyse > Descriptive Statistics > Frequencies > Statistics/Charts • Test of normal distribution (the K-S test) In SPSS: Analyse > Descriptive Statistics > Explore > Plots> Normality plots with tests
- 28.
- 29. Practice 1 • usingthe date file sample data 1.sav • conduct the descriptive statistics to explore (the variable named Intrinsic_Motivation_learn) mean, mode, median range, variance, standard deviation draw a histogram to see the frequency of scores
- 30. In SPSS Analyse >Descriptive Statistics > Frequencies
- 31.
- 32.
- 33.
- 34.
- 35. Practice 2 • usingthe date file sample data 1.sav • conduct the Kolmogorov-Smirnov (K-S) test and the Shapiro-Wilk test • Are the scores of the variable Intrinsic_Motivation_learn normally distributed?
- 36. In SPSS Analyse >Descriptive Statistics > Explore
- 37.
- 38. Test of normality:results According to the result, the Kolmogorov-Smirnov test and the Shapiro-Wilk test are highly significant, indicating that the distribution of scores for the variable Intrinsic_Motivation_learn is significantly different from a normal distribution. In other words, the distribution is not normal.
- 39. Practice 3 • usingthe date file SPSSexam.sav • conduct the Kolmogorov-Smirnov (K-S) test and the Shapiro-Wilk test for the variable exam 1. Are the scores of the variable exam normally distributed? 2. Redo the K-S test, this time organize the data by university (Hint: move the variable uni to the Factor List)