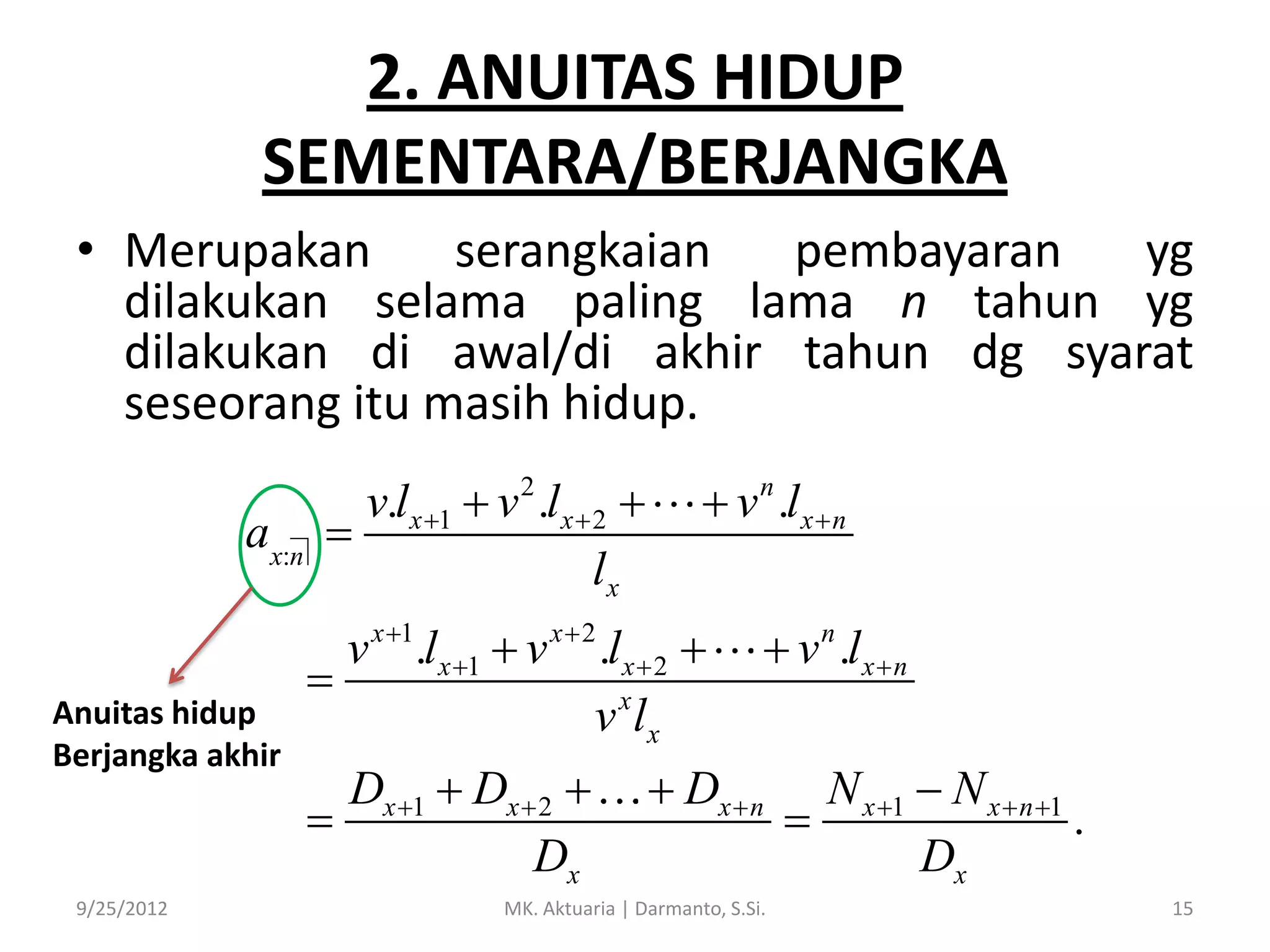
Dokumen tersebut membahas tentang anuitas hidup yang merupakan serangkaian pembayaran berkala yang dilakukan selama seseorang masih hidup. Terdapat tiga jenis anuitas hidup yang dijelaskan yaitu anuitas seumur hidup, anuitas sementara, dan anuitas ditunda.

1. ANUITAS HIDUP
9/25/2012
MK. Aktuaria | Darmanto, S.Si.
1

2. • Anuitas hidup adl serangkaian pembayaran
(besarnya
pembayaran
berkala
boleh
berubah) yang dilakukan selama seseorang
tertentu masih hidup.
• Pembayaran hanya dilakukan bila pada waktu
pembayaran itu jatuh orang tsb masih hidup.
9/25/2012
MK. Aktuaria | Darmanto, S.Si.
2

3. MACAM ANUITAS HIDUP
• ANUITAS SEUMUR HIDUP:
1. Anuitas awal seumur hidup: a x
adl serangkaian pembayaran sebesar 1 yg dilakukan tiap awal tahun,
pembayaran berlangsung seumur hidup seseorang tertentu.
2. Anuitas akhir seumur hidup: a x
adl serangkaian pembayaran sebesar 1 yg dilakukan tiap akhir tahun,
pembayaran berlangsung seumur hidup seseorang tertentu.
Simbol x menyatakan usia sekarang orang yg dengannya
anuitas tsb dikaitkan.
ax  ax  1
9/25/2012
MK. Aktuaria | Darmanto, S.Si.
3

4. • ANUITAS
SEMENTARA
(TEMPORARY ANNUITY):
/
BERJANGKA
1. Anuitas sementara awal tahun: a x:n
adl serangkaian pembayaran yg dilakukan selama paling
lama n tahun yg dilakukan di awal tahun dg syarat
seseorang itu masih hidup.
2. Anuitas sementara akhir tahun: a x:n
adl serangkaian pembayaran yg dilakukan selama paling
lama n tahun yg dilakukan di akhir tahun dg syarat
seseorang itu masih hidup.
ax:n  ax:n 1  1
9/25/2012
MK. Aktuaria | Darmanto, S.Si.
4

5. • ANUITAS DITUNDA:
1. Anuitas seumur hidup ditunda
 Anuitas seumur hidup ditunda awal tahun: n| a x
adl serangkaian pembayaran di awal tahun yg ditunda
n tahun selama seumur hidup jika seseorang itu masih
hidup.
 Anuitas seumur hidup ditunda akhir tahun: n| a x
adl serangkaian pembayaran di akhir tahun yg
ditunda n tahun selama seumur hidup jika seseorang
itu masih hidup.
9/25/2012
MK. Aktuaria | Darmanto, S.Si.
5

6. 2. Anuitas hidup sementara yang ditunda
 Anuitas sementara ditunda awal tahun: n|m ax
adl serangkaian pembayaran di awal tahun yg ditunda
n tahun selama paling lama m tahun jika seseorang itu
masih hidup.
 Anuitas sementara ditunda akhir tahun: n|m ax
adl serangkaian pembayaran di awal tahun yg ditunda
n tahun selama paling lama m tahun jika seseorang itu
masih hidup.
n 1
9/25/2012
ax 
n|
ax ; dan
n 1|m
MK. Aktuaria | Darmanto, S.Si.
ax 
n|m
ax
6

7. 1. ANUITAS SEUMUR HIDUP
• Misal setiap kohort (lx) yg menyetor sekarang
(tunai) sejumlah A rupiah pada suatu dana
sedemikian rupa sehingga tiap orang yg
mencapai usia x+1 menerima Rp. 1 dari dana
tsb, tiap orang yg mencapai usia x+2
menerima Rp. 1 dar dana tsb, demikian
seterusnya sampai sebanyak lx mati semua.
Berapakah besarnya A..?
9/25/2012
MK. Aktuaria | Darmanto, S.Si.
7

8. • Tiap orang menyetor A rupiah dan ada sebanyak
lx orang, jadi besarnya uang dalam dana sekarang
adl A.lx. Pada awal tahun berikutnya ada
sebanyak lx+1 orang yg masih hidup dan masing2
mendapatkan Rp.1, shg dana yg harus
dikeluarkan adalah lx+1. Dua tahun berikutnya
dana yg harus dikeluarkan adl lx+2, demikian
seterusnya. Jadi dapat ditulis,
Alx  v.lx1  v2 .lx2 
.
9/25/2012
MK. Aktuaria | Darmanto, S.Si.
 v w x .lw
8

9. • A disebut nilai tunai anuitas hidup akhir dari
seseorang dg pembayaran Rp. 1,- per tahun,
disebut pula premi tunggal bersih,
dilambangkan pula dengan a x
v.lx 1  v .lx  2 
A  ax 
lx
2
9/25/2012
MK. Aktuaria | Darmanto, S.Si.
v
w x
.lw
9

10. • Contoh:
Bila tingkat bunga 2,5% setahun, hitunglah a50 dg
menggunakan CSO 1941!
• Jawab:
1
v
 1, 0251
(1  0, 025)
1, 0251 (800.910)  1, 0252 (790.282)  ...  1, 02549
a50 
810.900
 15,316571
Tidak sulit tapi amat sangat membosankan >>> Dibuat simbol komutasi
9/25/2012
MK. Aktuaria | Darmanto, S.Si.
10

11. • SIMBOL-SIMBOL KOMUTASI:
Dx  v xlx
N x  Dx  Dx 1 
S x  N x  N x 1 
Cx  v x 1d x
M x  Cx  Cx 1 
Rx  M x  M x 1 
9/25/2012
MK. Aktuaria | Darmanto, S.Si.
11

12. • Didapatkan hubungan bahwa:
v.lx 1  v 2 .lx  2 
ax 
lx
 v w x .lw
v x 1.lx 1  v x  2 .lx  2 

v xlx
Dx 1  Dx  2 

Dx
 v w .lw
 Dw
N x 1

.
Dx
9/25/2012
MK. Aktuaria | Darmanto, S.Si.
12

13. • Karena
• Maka
ax  ax  1
N x 1
Dx  N x 1
ax 
1 
Dx
Dx
Dx  Dx 1  Dx  2 

Dx
 Dw
Nx

Dx
9/25/2012
MK. Aktuaria | Darmanto, S.Si.
13

14. – Contoh:
Hitunglah nilai tunai (premi tunggal bersih) suatu anuitas awal
seumur hidup dg pembayaran Rp. 1.500 setahun untuk
seseorang berusia 20 tahun jika i = 2,5% !
– Jawab:
Premi tunggal bersih
 1500.a20
N 20
15.744.215, 69
 1500
 1500
D20
580.662, 42
 Rp. 40.671,35
9/25/2012
MK. Aktuaria | Darmanto, S.Si.
14

15. 2. ANUITAS HIDUP
SEMENTARA/BERJANGKA
• Merupakan
serangkaian
pembayaran
yg
dilakukan selama paling lama n tahun yg
dilakukan di awal/di akhir tahun dg syarat
seseorang itu masih hidup.
ax:n
Anuitas hidup
Berjangka akhir
9/25/2012
v.lx 1  v 2 .lx  2 

lx

x 1
v .lx 1  v
x2
Dx 1  Dx  2 

Dx
 v n .lx  n
.lx  2 
v x lx
 v .lx  n
 Dx  n
MK. Aktuaria | Darmanto, S.Si.
n
N x 1  N x  n 1

.
Dx
15

16. • Karena: ax:n  ax:n1  1
• Didapatkan:
ax:n  ax:n 1  1
ax:n
v.lx 1  v 2 .lx  2 

lx
 v n 1.lx  n 1
v x 1.lx 1  v x  2 .lx  2 
 1
v x lx
v x lx  v x 1.lx 1  v x  2 .l x  2 

v x lx
9/25/2012
 v n 1.lx  n 1
 v n 1.l x  n 1
Dx  Dx 1   Dx  n 1 N x  N x  n


.
Dx
Dx
MK. Aktuaria | Darmanto, S.Si.
16

17. 3. ANUITAS HIDUP DITUNDA
• Ada 2:
1. Anuitas seumur hidup yang ditunda
2. Anuitas hidup sementara/berjangkan yang
ditunda
9/25/2012
MK. Aktuaria | Darmanto, S.Si.
17

18. 3.1. ANUITAS SEUMUR HIDUP
DITUNDA
• Adalah serangkaian pembayaran di awal/ di
akhir tahun yg ditunda n tahun selama seumur
hidup jika seseorang itu masih hidup.
Rp.1
x
9/25/2012
x+1
……
x+n
Rp.1
Rp.1
x+n+1
x+n+2
…..
MK. Aktuaria | Darmanto, S.Si.
18

19. • Nilai tunai untuk pembayaran di akhir tahun
(sebesar Rp.1) :
v n 1.lx  n 1  v n  2 .lx  n  2 
n| a x 
lx
 v w x .lw
v x  n 1.lx  n 1  v x  n  2 .lx  n  2 

v x lx
Dx  n 1  Dx  n  2 

Dx
9/25/2012
 Dw
MK. Aktuaria | Darmanto, S.Si.
 v w x .lw
N x  n 1

.
Dx
19

20. • Nilai tunai untuk pembayaran di awal tahun
(sebesar Rp. 1):
v n .lx  n  v n 1.lx  n 1 
n| a x 
lx
v x  n .lx  n  v x  n 1.lx  n 1 

v x lx
Dx  n  Dx  n 1 

Dx
9/25/2012
 Dw
MK. Aktuaria | Darmanto, S.Si.
 v w x .lw
 v w x .lw
N xn

.
Dx
20

21. • Didapatkan hubungan:
n|
ax  ax  ax:n

N x 1 N x 1  N x  n 1

Dx
Dx

N x  n 1
Dx
dan
n|
ax  ax  ax:n

N x N x  N xn

Dx
Dx
N xn

Dx
9/25/2012
MK. Aktuaria | Darmanto, S.Si.
21

22. 3.2. ANUITAS HIDUP BERJANGKA
DITUNDA
• adl serangkaian pembayaran di awal/ di akhir
tahun yg ditunda n tahun selama paling lama
m tahun (pembayaran terbatas hingga m
tahun) jika seseorang itu masih hidup.
masa pembayaran
masa penundaan
1
x
9/25/2012
1
x+n
MK. Aktuaria | Darmanto, S.Si.
1
x+n+m
tahun
22

23. • Nilai tunai untuk pembayaran di akhir tahun
(sebesar Rp. 1):
v n 1.lx  n 1  v n  2 .lx  n  2 
n|m ax 
lx
 v n  m .lx  n  m
v x  n 1.lx  n 1  v x  n  2 .lx  n  2 

v x lx
Dx  n 1  Dx  n  2 

Dx
9/25/2012
 v n  m .lx  n  m
N x  n 1  N x  n  m 1

.
Dx
 Dx  n  m
MK. Aktuaria | Darmanto, S.Si.
23

24. • Nilai tunai untuk pembayaran di akhir tahun
(sebesar Rp. 1):
n 1
v .lx  n  v .lx  n 1 
n|m ax 
lx
n
v x  n .lx  n  v x  n 1.lx  n 1 

v x lx
Dx  n  Dx  n 1 

Dx
9/25/2012
v
n  m 1
.lx  n  m 1
 v n  m 1.lx  n  m 1
 Dx  n  m 1
MK. Aktuaria | Darmanto, S.Si.
N xn  N xnm

.
Dx
24

25. • Diperoleh juga hubungan:
m|n
ax 
m 1|n
ax
N xm  N x mn

Dx
9/25/2012
MK. Aktuaria | Darmanto, S.Si.
25

26. ENDOWMEN MURNI
• Endowmen murni adl suatu pembayaran yg dilakukan
pada akhir suatu jangka waktu tertentu bagi seseorang
tertentu bila dia hidup mencapai akhir jangka waktu
tersebut. Bila orang tsb mati sebelum akhir jangka
waktu tsb maka tidak ada pembayaran sama sekali.
• Dilambangkan dengan nEx :: Artinya: nilai tunai
Endowmen Murni yg dikeluarkan bagi seorang berusia
x selama jangka waktu n tahun. Bila (x) mati sebelum
usia x+n thn maka tidak ada pembayaran, tapi bila dia
mencapai usia x+n maka kepadanya akan dibayarkan
sebesar 1 pada akhir tahun ke x+n.
9/25/2012
MK. Aktuaria | Darmanto, S.Si.
26

27. • Nilai tunai dari Rp. 1 adalah vn, peluangnya
dibayarkan adalah npx yaitu peluang (x)
mencapai usia x+n. Jadi,
lx  n v x  n .lx  n Dx  n
Ex  v n . n p x  v n .
 x

n
lx
v .lx
Dx
n|
ax
Anuitas awal seumur hidup yang ditunda selama n tahun dan
Pembayarannya hanya 1 kali sebesar Rp. 1,-.
9/25/2012
MK. Aktuaria | Darmanto, S.Si.
27

28. • Anuitas hidup berjangka akhir dapat
dipandang sbg gabungan dari serangkaian
endowment murni:
ax:n  1 Ex  2 Ex  3 Ex  ...  n Ex
Dx 1 Dx  2



Dx
Dx
Dx  n

Dx
Dx 1  Dx  2  ...  Dx  n N x 1  N x  n 1


.
Dx
Dx
9/25/2012
MK. Aktuaria | Darmanto, S.Si.
28

29. • Demikian juga:
m|n
ax 
m 1
Ex  m  2 Ex  m  3 Ex  ...  m  n Ex
Dx  m 1 Dx  m  2
Dx  m  n


 ... 
Dx
Dx
Dx
N x  m 1  N x  m  n 1

.
Dx
9/25/2012
MK. Aktuaria | Darmanto, S.Si.
29

30. SOAL - JAWAB
1. Hitunglah nilai tunai suatu endowmen murni
sebesar Rp. 1juta yg dikeluarkan bagi
seseorang berusia 25 thn selama 40 thn!
• Jawab:
D65
1.000.000 40 E25  1.000.000
D25
116.088,15
 1.000.000
506.594, 02
 Rp. 229.154,21.
9/25/2012
MK. Aktuaria | Darmanto, S.Si.
30

31. 2. Pada hari ulang tahunnya yg ke-30, si Ali membeli endowmen
murni sebesar Rp. 5.000,- untuk selama 35 thn. Bila dia
mencapai usia 65 thn, berapa besarkah yang akan dia
terima?
• Jawab:
35E30 adl nilai tunai dari 1, jd dgn nilai tunai Rp. 5.000,- Ali
akan dapat membeli endowmen murni dg besar pembayaran:
1. 35 E30  5.000
D30
5.000 5.000

 5.000
D65
D65
35 E30
D30
440.800,58
 5.000
 Rp. 18.985,60.
116.088,15
9/25/2012
MK. Aktuaria | Darmanto, S.Si.
31

32. 3. Si Ali, yg sekarang berusia 25 thn, ingin
membeli suatu rencana pensiun mulai usia
55 thn dg penerimaan 3 juta rupiah setahun.
Pembayaran pertama pada hari ulang
tahunnya yg ke-55. Untuk itu dia akan
melakukan pembayaran tahunan pada
permulaan tiap tahun mulai sekarang dan
berakhir pada hari ulang tahunnya yg ke-54.
Berapa besarkah pembayaran tahunan tsb?
9/25/2012
MK. Aktuaria | Darmanto, S.Si.
32

33. • Jawab:
Nilai tunai dari penerimaan tahunan sebesar 3jt
bagi seseorang berusia 25thn ditunda 30thn
adalah
3.000.000 30| a25
N55
 3.000.000
D25
Untuk membeli ini si Ali harus melakukan
pembayaran yg berbentuk anuitas sementara.
Misalkan pembayaran tahunannya adl B, maka
nilai tunai anuitas tsb adl
B.a25:30
9/25/2012
N 25  N55
B
D25
MK. Aktuaria | Darmanto, S.Si.
33

34. • Dengan menyamakan kedua nilai tunai anuitas
tsb maka nilai B dapat diperoleh:
N 25  N 55
N 55
B
 3.000.000
D25
D25
N 55
B  3.000.000
N 25  N 55
2.754.768, 79
 3.000.000
12.992.619,10  2.754.768, 79
 Rp. 807.230,63.
9/25/2012
MK. Aktuaria | Darmanto, S.Si.
34

35. 4. Pada usia 65 si Ali mpy dua pilihan:
a) Menerima 25jt dari suatu perusahaan asuransi yg akan
membungakannya dg i = 2,5% setahun, dan dia akan
menerima dg cara tentu tiap permulaan tahun selama
20thn (anuitas tentu selama 20thn) sejumlah uang yg
sama besarnya dan sesudah 20 kali pembayaran dana tadi
habis.
b) Membiarkan uangnya pd perusahaan tadi dan menerima
jumlah uang sama besarnya tiap permulaan tahun selama
20thn bila dia hidup (anuitas hidup).
Hitunglah besarnya penerimaan si Ali tiap tahun dalam kedua
hal tsb. Bila si Ali mati tepat sebelum mencapai usia 80thn,
berapa besarkah yg akan diterima oleh ahli warisnya?
9/25/2012
MK. Aktuaria | Darmanto, S.Si.
35

36. • Misalkanlah penerimaan tahunan si Ali Rp. B
a) Nilai tunai anuitas awal tentu selama 20 thn dg
pembayaran B tiap tahun adl
Ba20  25.000.000
Ba20
1 v
B
iv
20

1 1
1, 025
B
(0, 025) 1
1, 025
B  25.000.000


(0, 025) 1
1, 025

1 1
1, 025
9/25/2012

20


20
MK. Aktuaria | Darmanto, S.Si.

 Rp. 1.564.564,12
36

37. • Bila si Ali mati tepat sebelum berusia 80 tahun maka masih tersisa 5 kali
pembayaran yg hrs dilaksanakan yg akan diterima oleh si Ali. Nilai tunai
sisa pembayarannya adl:
1.564.564,12 a5  Rp. 7.450.413,93
b. Pembayaran tahunan untuk anuitas hidup awal berjangka pada usia 65thn
selama 20 thn adl
Ba65:20
N65  N85
B
 25.000.000
D65
B  25.000.000
D65
 Rp. 2.557.820,58
N65  N85
Dalam hal ini jika si Ali mati maka ahli waris tidak mendapat apa-apa.
9/25/2012
MK. Aktuaria | Darmanto, S.Si.
37