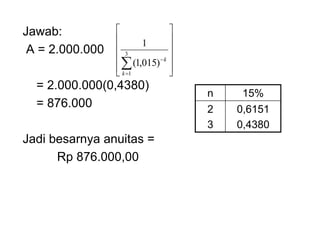
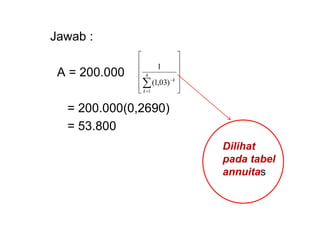
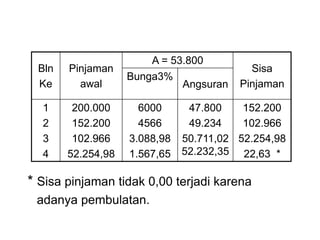
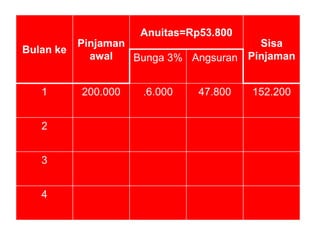
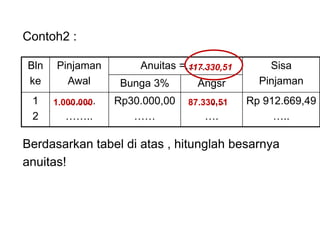
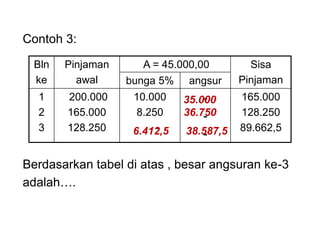
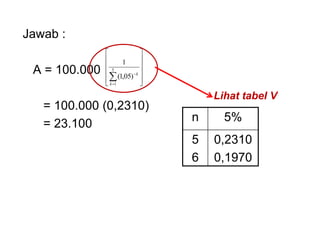
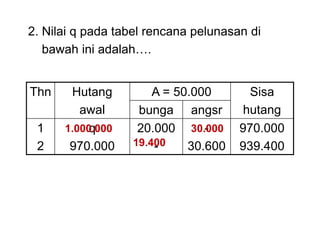
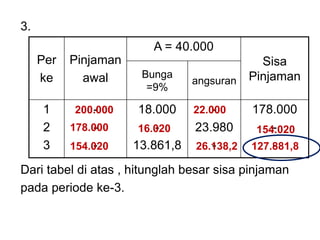
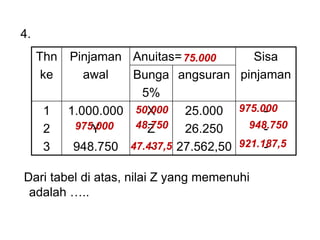
Dokumen tersebut membahas tentang anuitas, yaitu pembayaran berkala dengan jumlah yang sama yang terdiri dari bagian bunga dan angsuran pokok. Dokumen tersebut menjelaskan rumus-rumus untuk menghitung besaran anuitas, rencana pelunasan, sisa pinjaman, dan contoh soalnya.

1. ANUITAS

2. Anuitas adalah sejumlah pembayaran yang
sama besarnya, yang dibayarkan setiap
akhir jangka waktu, dan terdiri atas
bagian
bunga dan bagian angsuran.

3. Jika besarnya anuitas adalah A, angsuran
periode ke-n dinyatakan dengan an, dan
bunga periode ke-n adalah bn, maka dipero-
leh hubungan:
A = an + bn , n = 1,2,3,..

4. * Menghitung anuitas
Dengan notasi sigma:
A = M
Contoh:
Pinjaman sebesar Rp 2.000.000,00 akan diluna
si dengan sistem anuitas selama 3 tahun. Anui-
tas pertama dibayar satu tahun setelah peneri-
maan uang. Jika bunga diperhitungkan 15%
setahun, besarnya anuitas adalah….




n
k
k
i
1
)
1
(
1

5. Jawab:
A = 2.000.000
= 2.000.000(0,4380)
= 876.000
Jadi besarnya anuitas =
Rp 876.000,00
n 15%
2
3
0,6151
0,4380















3
1
)
015
,
1
(
1
k
k

6. * Membuat tabel rencana pelunasan
Contoh1:
Pinjaman sebesar Rp 200.000,00 akan dilu-
nasi dengan 4 anuitas bulanan . Anuitas
pertama dibayar satu bulan setelah
penerimaan uang. Jika bunga 3% sebulan,
buatlah tabel rencana pelunasannya!

7. Jawab :
A = 200.000
= 200.000(0,2690)
= 53.800















4
1
)
03
,
1
(
1
k
k
Dilihat
pada tabel
annuitas

8. * Sisa pinjaman tidak 0,00 terjadi karena
adanya pembulatan.
Bln
Ke
Pinjaman
awal
A = 53.800
Sisa
Pinjaman
Bunga3%
Angsuran
1
2
3
4
200.000
152.200
102.966
52.254,98
6000
4566
3.088,98
1.567,65
47.800
49.234
50.711,02
52.232,35
152.200
102.966
52.254,98
22,63 *

9. Bulan ke
Pinjaman
awal
Anuitas=Rp53.800
Sisa
Pinjaman
Bunga 3% Angsuran
1 200.000 .6.000 47.800 152.200
2
3
4

10. Contoh2 :
Berdasarkan tabel di atas , hitunglah besarnya
anuitas!
Bln
ke
Pinjaman
Awal
Anuitas =.... … Sisa
Pinjaman
Bunga 3% Angsr
1
2
……..
……..
Rp30.000,00
……
…..
….
Rp 912.669,49
…..
1.000.000 87.330,51
117.330,51

11. Jawab :
Pinjaman awal bln ke-1 = 30.000 x 100/3
= 1.000.000
Angsuran bln ke-1 = Pinj awal-Sisa Pinj
(a1) = 1.000.000- 912.669,49
= 87.330,51
Anuitas = a1 + b1
= 87.330,51 + 30.000
= 117.330,51

12. Contoh 3:
Berdasarkan tabel di atas , besar angsuran ke-3
adalah….
Bln
ke
Pinjaman
awal
A = 45.000,00 Sisa
Pinjaman
bunga 5% angsur
1
2
3
200.000
165.000
128.250
10.000
8.250
-
-
-
-
165.000
128.250
89.662,5
35.000
36.750
6.412,5 38.587,5

13. Jawab:
Bunga bln ke-3(b3) = 5% x 128.250
= 6.412,5
Angsuran ke-3 (a3) = 45.000 – 6.412,5
= 38.587,5
* Atau a3 = Pinj awal – sisa pinj
= 128.250 - 89.662,5 = 38.587,5
Jadi besar angsuran ke-3 = Rp 38.587,5

14. *Menghitung Pelunasan Hutang
Jika pelunasan (angsuran) dalam anuitas ke-1
adalah a1, dalam anuitas ke-n adalah an, hutang
semula M dan suku bunganya i, maka :
an = a1(1+i)n-1 , an = ak (1+i)n-k

15. Contoh:
Suatu pinjaman sebesar Rp 5.000.000,00
dengan bunga 6% per bulan akan dilunasi
dengan anuitas bulanan sebesar
Rp 500.000,00 .Dengan menggunakan tabel
berikut , hitunglah besar angsuran ke-3.
n 6%
2
3
1,1236
1,1910

16. Jawab:
a1 = A - b1 = 500.000 – 6%(5.000.000)
= 500.000 – 300.000
= 200.000
a3 = a1(1+i)3-1
= 200.000(1,06)2
= 200.000(1,1236)
= 224.720
Jadi besar angsuran ke-3 = Rp 224.720,00
n 6%
2
3
1,1236
1,1910

17. * Menghitung Sisa Pinjaman
Sisa pinjaman setelah pembayaran anuitas
ke-m (m<n) dapat dihitung dengan cara:
1. Sisa pinjaman = besar pinjaman – jumlah
semua angsuran yang sudah dibayar
Sm = M – a1 






 


1
1
)
1
(
1
m
k
k
i

18. 2. Sisa Pinjaman = jumlah semua nilai tunai
yang belum dibayar, dihitung pada akhir
tahun pembayaran anuitas terakhir yang
dibayar
Sm = A 










m
n
k
k
i
1
)
1
(

19. 3. Hubungan antara bunga dengan sisa
pinjaman, yaitu :
Sm =
i
b m )
1
( 

20. Contoh :
Seseorang meminjam uang sebesar
Rp 1.000.000,00 yang akan dilunasinya
dalam 12 anuitas bulanan. Anuitas pertama
dibayar sebulan setelah penerimaan pinja
man, dengan suku bunga majemuk 3%
sebulan.Hitunglah sisa pinjaman setelah
anuitas ke-9!

21. Jawab :
A = 1.000.000 = 1.000.000(0,100462)
= 100.462
S9 = 100.462
= 100.462 (2,828611)
= 284.167,92















12
1
)
03
,
1
(
1
k
k
k
k



  )
03
,
0
1
(
9
12
1
Lihat tabel IV

22. Latihan:
1. Suatu pinjaman dengan suku bunga 5%
per bulan sebesar Rp 100.000,00 akan
dilunasi dengan 5 anuitas bulanan. Jika
anuitas pertama dibayar sebulan setelah
pinjaman diterima,maka besar anuitas
tersebut adalah….

23. Jawab :
A = 100.000
= 100.000 (0,2310)
= 23.100















5
1
)
05
,
1
(
1
k
k
n 5%
5
6
0,2310
0,1970
Lihat tabel V

24. 2. Nilai q pada tabel rencana pelunasan di
bawah ini adalah….
Thn Hutang
awal
A = 50.000 Sisa
hutang
bunga angsr
1
2
q
970.000
20.000
-
-
30.600
970.000
939.400
30.000
1.000.000
19.400

25. Jawab:
a1 = A – b1 = 50.000- 20.000
= 30.000
Hutang awal thn ke-1 (q) = a1 + sisa htg
= 30.000 + 970.000
= 1.000.000
Jadi nilai q = Rp 1.000.000,00

26. 3.
Dari tabel di atas , hitunglah besar sisa pinjaman
pada periode ke-3.
Per
ke
Pinjaman
awal
A = 40.000
Sisa
Pinjaman
Bunga
=9%
angsuran
1
2
3
-
-
-
18.000
-
13.861,8
-
23.980
-
178.000
-
-
22.000
200.000
178.000 16.020 154.020
154.020 26.138,2 127.881,8

27. Jawab :
Pinjaman awal periode ke-2 = 178.000
Sisa pinjaman periode ke-2 = Pinjaman awal – a2
= 178.000 – 23.980
= 154.020
Pinjaman awal periode ke-3 = 154.020
a3 = A – b3 = 40.000 – 13.861,8
= 26.138,2
Sisa pinjaman periode ke- 3 = Pinj awal – a3
= 154.020 – 26.138,2 = 127.881,8

28. 4.
Dari tabel di atas, nilai Z yang memenuhi
adalah …..
Thn
ke
Pinjaman
awal
Anuitas= Sisa
pinjaman
Bunga
5%
angsuran
1
2
3
1.000.000
Y
948.750
X
Z
-
25.000
26.250
27.562,50
-
-
-
50.000 975.000
975.000 48.750 948.750
75.000
47.437,5 921.187,5

29. Jawab :
Sisa pinjaman thn ke-1 = pinj awal – a1
= 1.000.000 – 25.000
= 975.000
Pinjaman awal thn ke- 2 (Y) = 975.000
Bunga thn ke-2 (Z) = 5% x 975.000
= 48.750
Jadi besar bunga thn ke-2 = Rp 48.750,00

30. 5. Pada pelunasan pinjaman
dengan
anuitas, diketahui suku
bunganya 2%
sebulan. Jika angsuran
bulan ke-3
Rp 67.300,00, maka
besarnya angsuran
bulan ke-5 adalah….

31. Jawab :
a5 = a3 (1+i)5-3
= 67.300(1,02)2
= 67.300(1,0404)
= 70.018,92
Jadi besar angsuran bulan ke- 5
adalah Rp 70.018,92
Tabel I

32. 6. Pinjaman sebesar Rp 100.000,-
akan dilunasi dengan anuitas
tahunan sebesar Rp 21.630,00
berdasarkan suku bunga
majemuk 8% setahun.
Angsuran pertama dilaksanakan
satu tahun setelah
penerimaan pinjaman,
sisa pinjaman setelah
angsuran pertama dibayar =

33. Jawab:
a1 = A – b1
= 21.630 – x 100.000
= 21.630 – 8.000
= 13.630
S1 = A – a1 = 100.000 – 13.630
= 86.370
Jadi sisa pinjaman setelah angsuran pertama
adalah Rp 86.370,00
100
8