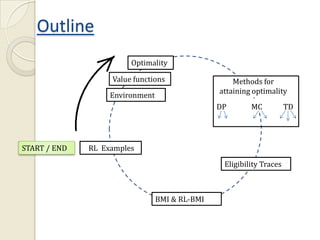
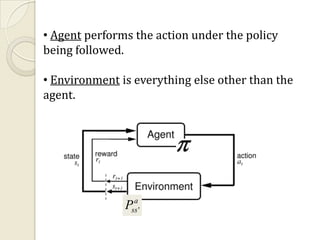
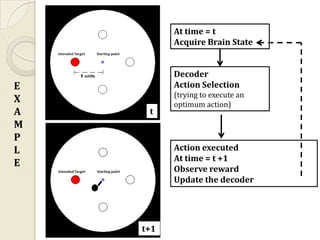
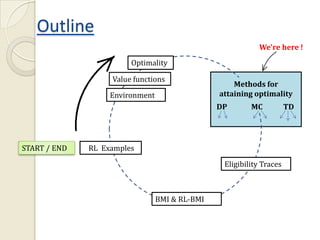
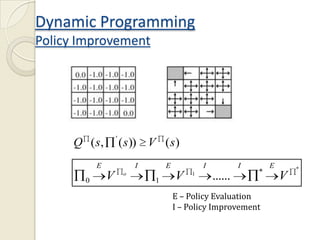
This document provides an introduction to reinforcement learning (RL) and RL for brain-machine interfaces (RL-BMI). It outlines key RL concepts like the environment, value functions, and methods for achieving optimality including dynamic programming, Monte Carlo, and temporal difference methods. It also discusses eligibility traces and provides an example of an online/closed-loop RL-BMI architecture. References for further reading on the topics are included.

1. An Introduction to Reinforcement
Learning (RL) and RL Brain Machine
Interface (RL-BMI)
Aditya Tarigoppula
www.joefrancislab.com
SUNY Downstate Medical Center

2. Outline
Optimality
Value functions Methods for
attaining optimality
Environment
DP MC TD
START / END RL Examples
Eligibility Traces
BMI & RL-BMI

4.  Environment model - Markov decision process
1) States ‘S’
2) Actions ‘A’
3) State transition probabilities.
a
Pss ' Pr{st 1 s ' | st s, at a}, Pa 1
ss '
4) Reward s'
Rt rt 1 rt 2 rt 3 ... rt T
2
Rt rt 1 rt 2 rt 3 ...
0 1
5) :s a
Deterministic, non-stationary policy
 RL Problem: The decision maker, ‘agent’ needs to learn the
optimum policy in an ‘environment’ to maximize the total
amount of reward it receives over the long term.

5. • Agent performs the action under the policy
being followed.
• Environment is everything else other than the
agent.
a
Pss '

6. Value Functions:
 State Value Function
V ( s) E {Rt | st s}
k
E {rt 1 rt k 2 | st s}
k 0
a a
( s, a ) Pss ' [ Rss ' V ( s ' )]
a s'
 State – Action Value Function
Q ( s, a ) E {Rt | st s, at a}
k
E { rt k 1 | st s, at a}
k 0

7. Optimal Value Function:
 Optimal Policy – A policy that is better than or equal to all
the other policies is called Optimal policy.
(in the sense of maximizing expected reward)
 Optimal state value function
V * ( s) maxV ( s)
 Optimal state-action value function
Q* ( s, a) max Q ( s, a)
 Bellman optimality equation
V * ( s) max E{rt 1 V * ( s' ) | st s, at a}
a
Q * ( s, a ) E{rt 1 max Q* ( s' , a' ) | st s, at a}
a

8. At time = t
Acquire Brain State
Decoder
E Action Selection
(trying to execute an
X optimum action)
A t
M
P
L Action executed
At time = t +1
E
Observe reward
Update the decoder
t+1

9. S1
Pr 0.8
E S3 Pr 0.1 Pr 0.1 S2
X
A
M Pr 0
P S4
L
E
V ( s) [0.8 * ( R( s, a1 ) *V ( s1 )) 0.1* ( R( s, a2 )...
... *V ( s2 )) 0.1* ( R( s, a3 ) *V ( s3 ))]
Prof. Andrew Ng, Lecture
16, Machine learning

10. Outline
We're here !
Optimality
Value functions
Methods for
Environment attaining optimality
DP MC TD
START / END RL Examples
Eligibility Traces
BMI & RL-BMI

11. Solution Methods for RL problem
◦ Dynamic Programming (DP) – is a method for optimization of
problems which exhibit the characteristics of overlapping sub
problems and optimal substructure.
◦ Monte Carlo method (MC) - requires only experience--sample
sequences of states, actions, and rewards from interaction
with an environment.
◦ Temporal Difference learning (TD) – is a method that
combines the better aspects of DP (estimation) and MC
(experience) without incorporating the ‘troublesome’ aspects
of both.

12. Dynamic Programming
Policy Evaluation

13. Dynamic Programming
Policy Improvement
'
Q ( s, ( s )) V ( s )
E I E I I E *
*
0 V o
1 V 1
...... V
E – Policy Evaluation
I – Policy Improvement

14. Policy Iteration Value Iteration
D
Y
N
A
M
I
C
P
R
O Replace entire
G section with
R
A V (s) max a a
Pss ' [ Rss ' V ( s ' )]
a
M s'
M
I
N
G

15. Monte Carlo Vs. DP
◦ The estimates for each state are independent. In other words,
MC methods do not "bootstrap“.
◦ DP includes only one-step transitions
whereas the MC diagram goes all the
way to the end of the episode.
◦ The computational expense of estimating the value of a single
state is less when one requires the value of only a subset of
the states.

16. Monte Carlo
 Policy Evaluation
Every visit MC First visit MC

17. -> Without a model, we need Q value estimates.
-> All state-action pairs should be visited.
-> Exploration techniques
1) Exploring starts 2) e-greedy Policy
Next Slide
M
O
N
T
E
C
A
R
L
O

18.  As promised, this is the “NEXT SLIDE” !
M
O
N
T
E
C
A
R
L
O

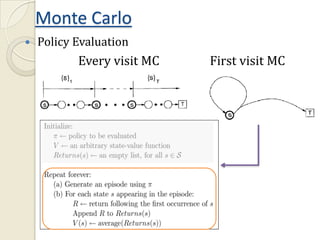
19. Temporal Difference Methods
◦ Like MC, TD methods can learn directly from raw experience
without a model of the environment's dynamics. Like DP, TD
methods update estimates are based in part on other learned
estimates, without waiting for a final outcome (they bootstrap).
V ( st ) V ( st ) [rt 1 V ( st 1 ) V ( st )]

20. TD(lambda)
Bias –Variance Tradeoff
Bias decreases
Intuition: start with large
‘lamda’ and then decrease
over time
Variance Increases
 trace decay parameter

21. SARSA
Difference
Q Learning

22. Outline
Optimality
Value functions Methods for
attaining optimality
Environment
DP MC TD
START / END RL Examples
Eligibility Traces
We're here !
BMI & RL-BMI

23. Eligibility Traces
OR

24. Outline
Optimality
Value functions Methods for
attaining optimality
Environment
DP MC TD
START / END RL Examples
Eligibility Traces
BMI & RL-BMI
We're here !

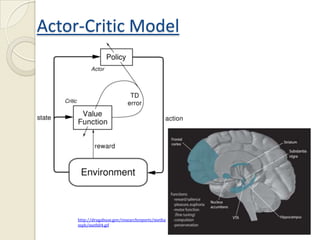
25. Online/closed loop RL-BMI architecture
NEURAL action output _ index[max(Qi ( st ))]
SIGNAL
Q( st , at ) Qi ( st , action)
reward
tanh(.)
TD _ err rt * Q( st 1 , at 1 ) Q( st , at )
delta TD _ err * e _ trace
‘delta’ used for updating
the weights through
back-propagation

26. B
M
I
S
E
T
U
P
Scott, S. H. (1999). "Apparatus for measuring and
perturbing shoulder and elbow joint positions and
torques during reaching." J Neurosci Methods
89(2): 119-27.

28. Actor-Critic Model
http://drugabuse.gov/researchreports/metha
mph/meth04.gif

29. References
 Reinforcement Learning: An Introduction
Richard S. Sutton & Andrew G. Barto
 Prof. Andrew Ng’s machine Learning Lectures
 http://heli.stanford.edu
 Dr. Joseph T. Francis
www.joefrancislab.com
 Prof. Peter Dayan
 Dr. Justin Sanchez Group
http://www.bme.miami.edu/nrg/