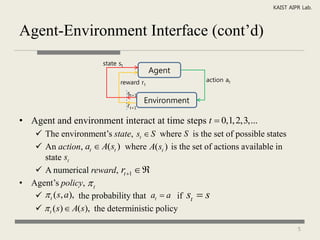
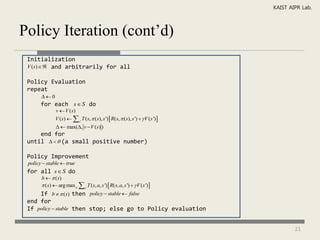
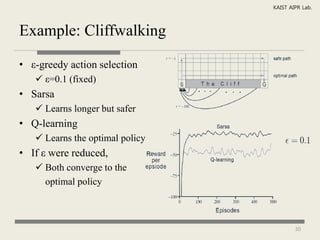
The document discusses reinforcement learning and Markov decision processes. It introduces reinforcement learning as an approach to machine learning where an agent learns to take actions in an environment to maximize rewards. Markov decision processes are described as a framework involving states, actions, transitions between states, and rewards. The goals of reinforcement learning are to learn a policy that maps states to optimal actions to maximize long-term rewards.

1. Reinforcement Learning: An Introduction
Ch. 3, 4, 6
R. Sutton and A. Barto.
KAIST AIPR Lab.
Jung-Yeol Lee
3rd June 2010
1

2. KAIST AIPR Lab.
Contents
• Reinforcement learning
• Markov decision processes
• Value function
• Policy iteration
• Value iteration
• Sarsa
• Q-learning
2

3. KAIST AIPR Lab.
Reinforcement Learning
• An approach to machine learning
• How to take actions in an environment responding to those
actions and presenting new situations
• To find a policy that maps situations to the actions
• To discover which action yield the most reward signal over the
long run
3

4. KAIST AIPR Lab.
Agent-Environment Interface
• Agent
 The learner and decision maker
• Environment
 Everything outside the agent
 Responding to actions and presenting new situations
 Giving a reward (feedback, or reinforcement)
4

5. KAIST AIPR Lab.
Agent-Environment Interface (cont’d)
state st
Agent
reward r t action at
st+1
Environment
r t+1
• Agent and environment interact at time steps t  0,1, 2,3,...
 The environment’s state, st  S where S is the set of possible states
 An action, at  A(st ) where A( st ) is the set of actions available in
state st
 A numerical reward, rt 1 
• Agent’s policy,  t
  t ( s, a), the probability that at  a if st  s
  t (s)  A(s), the deterministic policy
5

6. KAIST AIPR Lab.
Goals and Rewards
• Goal
 What we want to achieve, not how we want to achieve it
• Rewards
 To formalize the idea of a goal
 A numerical value by the environment.
6

7. KAIST AIPR Lab.
Returns
• Specific function of the reward sequence
• Types of returns
 Episodic tasks
Rt  rt 1  rt 2  rt 3   rT , where T is a final time step
 Continuing tasks ( T   )
The additional concept, discount rate 

Rt  rt 1   rt  2   rt 3 
2
   k rt  k 1 , where 0    1
k 0
7

8. KAIST AIPR Lab.
Exploration vs. Exploitation
• Exploration
 To discover better action selections
 To improve its knowledge
• Exploitation
 To maximize its reward based on what it already knows
• Exploration-exploitation dilemma
 Both can’t be pursued exclusively without failing
8

9. KAIST AIPR Lab.
Markov Property
• State signal retaining all relevant information
• “Independence of path” property
• Formally,
 Pr st 1  s ', rt 1  r | st , at , rt , st 1 , at 1 , , r1 , s0 , a0 
 Pr st 1  s ', rt 1  r | st , at 
9

10. KAIST AIPR Lab.
Markov Decision Processes (MDP)
• 4-tuple, (S , A, T , R)
 S is a set of states
 A is a set of actions
 Transition probabilities
T (s, a, s ')  Pr st 1  s ' | st  s, at  a , for all s, s '  S , a  A(s)
 The expected reward
R(s, a, s ')  E rt 1 | st  s, at  a, st 1  s '
• Finite MDP: the state and action spaces are finite
10

11. KAIST AIPR Lab.
Example: Gridworld
• S  1, 2,...,14
• A  up, down, right , left
• E.g., T (5, right ,6)  1, T (5, right ,10)  0, T (7, right ,7)  1
• R(s, a, s ')  1, s, s ', a
11

12. KAIST AIPR Lab.
Value Functions
• “How good” it is to perform a given action in a given state
• The value of a state s under a policy 
 The state-value function for policy
• Expected return when starting in s and following 
 k 
V ( s)  E Rt | st  s  E   rt  k 1 | st  s 

 k 0 
 The action-value function for policy 
• Expected return starting from s , taking the action a and following 
 k 
Q ( s, a)  E Rt | st  s, at  a  E   rt  k 1 | st  s, at  a 

 k 0 
12

13. KAIST AIPR Lab.
Bellman Equation
• Particular recursive relationships of value functions
• The Bellman equation for V 
 V ( s)  E   rt  k 1 | st  s 
  k

 k 0 
 

 E rt 1     k rt  k  2 | st  s 
 k 0 
 

   ( s, a) T ( s, a, s ')  R( s, a, s ')   E {  k rt  k  2 | st 1  s '}
a s'  k 0 
   ( s, a) T ( s, a, s ')  R( s, a, s ')   V  ( s ') 
 
a s'
• The value function is the unique solution to its Bellman equation
13

14. KAIST AIPR Lab.
Optimal Value Functions
• Policies are partially ordered
   ' if and only if V  (s)  V  ' (s) for all s  S
• Optimal policy π*
 Policies that is better than or equal to all other policies
• Optimal state-value function V *
 V * (s)  max V  ( s), for all s  S

• Optimal action-value function Q*
 Q* (s, a)  max Q ( s, a), for all s  S and a  A(s)

 E rt 1   V * (st 1 ) | st  s, at  a
14

15. KAIST AIPR Lab.
Bellman Optimality Equation
• The Bellman equation for V *
*
V ( s)  max Q ( s, a)
*
aA( s )
 max E * Rt | st  s, at  a
a
 k 
 max E *   rt  k 1 | st  s, at  a 
a
 k 0 
 

 max E * rt 1     k rt  k  2 | st  s, at  a 
a
 k 0 
 max E rt 1   V * (st 1 ) | st  s, at  a
a
 max  T ( s, a, s ')  R( s, a, s ')   V * ( s ') 
 
a
s'
15

16. KAIST AIPR Lab.
Bellman Optimality Equation (cont’d)
• The Bellman optimality equation for Q*

 Q* (s, a)  E rt 1   max Q* (st 1 , a ') | st  s, at  a
a'

  T (s, a, s ')  R( s, a, s ')   max Q* ( s ', a ') 
s'
 a' 
• Optimal policy from Q*
  * (s)  arg max Q* (s, a)
aA( s )
• Optimal policy from V *
 Any policy that is greedy with respect to V * (s)  max Q (s, a)
*
aA( s )
16

17. KAIST AIPR Lab.
Dynamic Programming (DP)
• Algorithms for optimal policies under a perfect model
• Limited utility in reinforcement learning, but theoretically
important
• Foundation for the understanding of other methods
17

18. KAIST AIPR Lab.
Policy Evaluation
• How to compute the state-value function V 
• Recall, the Bellman equation for V 
 V (s)    ( s, a) T ( s, a, s ')  R( s, a, s ')   V ( s ') 
 
 
a s'
• A sequence of approximate value functions V0 ,V1 ,V2 ,
• Successive approximation
 Vk 1 ( s)   T ( s, a, s ')  R( s, a, s ')   Vk ( s ') 
s'
• Vk converge to V  as k  
18

19. KAIST AIPR Lab.
Policy Improvement
• Policy improvement theorem (proof)
 If Q (s,  '(s))  V  (s), for all s  S then, V  ' (s)  V  (s)
 Better to switch action iff Q (s,  '(s))  V  (s)
• The new greedy policy,  '
 Selecting the action that appears best
 '(s)  arg max Q ( s, a)
a
 arg max  T ( s, a, s ')  R( s, a, s ')   V  ( s ') 
 
a
s'
• What if V  '  V  ?
 Both  ' and  are optimal policies
19

20. KAIST AIPR Lab.
Policy Iteration
•  0  V   1  V    2    *  V * ,
E
 0 I
 E1
 I
 E
 I
 E

where  denotes a policy evaluation and
E

 denotes a policy improvement
I

• Policy iteration finishes when a policy is stable
20

21. KAIST AIPR Lab.
Policy Iteration (cont’d)
Initialization
V (s)  and arbitrarily for all
Policy Evaluation
repeat
0
for each s  S do
v  V (s)
V (s)   s ' T (s,  (s), s ')  R(s,  ( s), s ')   V ( s ') 
  max(, v  V (s) )
end for
until    (a small positive number)
Policy Improvement
policy  stable  true
for all s  S do
b   ( s)
 (s)  arg max a  s ' T (s, a, s ')  R(s, a, s ')   V (s ')
If b   (s) then policy  stable  false
end for
If policy  stable then stop; else go to Policy evaluation
21

22. KAIST AIPR Lab.
Value Iteration
• Turning the Bellman optimality equation into an update rule
 Vk 1 (s)  max E rt 1   Vk (st 1 ) | st  s, at  a
a
 max  T ( s, a, s ')  R(s, a, s ')   Vk (s ')  for all s  S
a
s'
• Policy π, such that
 (s)  arg max  T ( s, a, s ')  R( s, a, s ')   V ( s ') 
a s'
22

23. KAIST AIPR Lab.
Value Iteration (cont’d)
Initialization V arbitrarily, e.g., V (s)  0 for all s  S 
repeat
0
for each s  S do
v  V (s)
V (s)  max a  s ' T (s, a, s ')  R(s, a, s ')   V (s ')
  max(, v  V (s) )
end for
until    (a small positive number)
Output a deterministic policy,  , such that
 (s)  arg max a  s ' T (s, a, s ')  R(s, a, s ')   V (s ')
23

24. KAIST AIPR Lab.
Temporal-Difference (TD) Prediction
• Model free method
• Basic Update rule
 NewEstimate  OldEstimate  StepSize Target  OldEstimate
• The simplest TD method, TD(0) error
 V (st )  V (st )    Rt  V (st )
 V (st )    rt 1   V (st 1 )  V (st )
 α: step size
24

25. KAIST AIPR Lab.
Advantages of TD Prediction Methods
• Bootstrapping
 Estimate on the basis of other estimates (a guess from a guess)
• Over DP methods
 Model free methods
• Wait only one time step
 In case of continuing tasks and no episodes
• Guarantee convergence to the correct answer
 Sufficiently small α
 Selecting all actions infinitely often
25

26. KAIST AIPR Lab.
Sarsa: On-Policy TD Control
• On-policy
 Improve the policy that is used to make decisions

• Estimate Q under the current policy π
• Under TD(0), apply to the corresponding algorithm
 Q(st , at )  Q(st , at )   rt 1   Q(st 1, at 1 )  Q(st , at ) 
 For every quintuples of events, (st , at , rt 1 , st 1 , at 1 ) (Sarsa)
 If st 1 is terminal, then Q(st 1 , at 1 )  0
• Change π toward greediness w.r.t. Q
• Converges if all pairs are visited infinite times and policy
converges to the greedy (e.g., ε= t in ε-greedy)
1
26

27. KAIST AIPR Lab.
Sarsa: On-Policy TD Control (cont’d)
Initialize Q(s, a) arbitrarily
Repeat (for each episode):
Initialize s
Choose a from s using policy derived from Q (e.g., ε-greedy)
Repeat (for each step of episode):
Take action a, observe r , s '
Choose( a ' from s ' using policy derived from Q(e.g., ε-greedy)
Q(s, a)  Q(s, a)    r   Q(s ', a ')  Q(s, a)
s  s '; a  a '
until s is terminal
27

28. KAIST AIPR Lab.
Q-Learning: Off-Policy TD Control
• Off-policy
 Behavior policy
 Estimation policy (may be deterministic (e.g., greedy) )
• Simplest form, one-step Q-learning, is defined by
 Q( st , at )  Q( st , at )   rt 1   max Q( st 1 , a)  Q( st , at ) 
 a 
• Directly approximate Q*, the optimal action-value function
• Qt converges to Q* with probability 1
 Correct converges if all pairs continue to be updated
28

29. KAIST AIPR Lab.
Q-Learning: Off-Policy TD Control (cont’d)
Initialize Q(s, a) arbitrarily
Repeat (for each episode):
Initialize s
Repeat (for each step of episode):
Choose( a from s using policy derived from Q (e.g., ε-greedy)
Take action a, observe r , s '
Q(s, a)  Q(s, a)    r   max a ' Q(s ', a ')  Q(s, a)
s  s'
until s is terminal
29

30. KAIST AIPR Lab.
Example: Cliffwalking
• ε-greedy action selection
 ε=0.1 (fixed)
• Sarsa
 Learns longer but safer
• Q-learning
 Learns the optimal policy
• If ε were reduced,
 Both converge to the
optimal policy
30

31. KAIST AIPR Lab.
Summary
• Goal of reinforcement learning
 To find an optimal policy to maximize the long-term reward
• Model-based methods
 Policy iteration: a sequence of improving policies and value
function
 Value iteration: backup operations for V *
• Model-free methods

 Sarsa estimates Q for the behavior policy  , change  toward
greediness w.r.t. Q
 Q-learning directly approximates the optimal action-value
function
31

32. KAIST AIPR Lab.
References
[1] R. Sutton and A. Barto. Reinforcement Learning: An
Introduction. Pages 51-158, 1998.
[2] S. Russel and P. Norvig. Artificial Intelligence: A Modern
Approach. Pages 613-784, 2003.
32

33. KAIST AIPR Lab.
Q&A
• Thank you
33

34. KAIST AIPR Lab.
Appendix 1. Policy Improvement Theorem
• Proof)
34

35. KAIST AIPR Lab.
Appendix 2. Convergence of Value Iteration
• Prove
35

36. KAIST AIPR Lab.
Appendix 3. Target Estimation
• DP • Simple TD
V (st )  E  rt 1   V (st 1 ) V (st )  V (st )    rt 1   V (st 1 )  V (st )
36