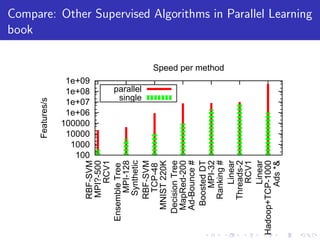
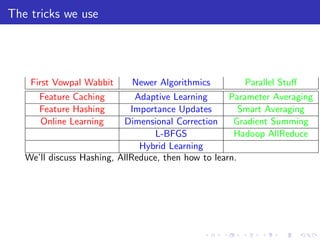
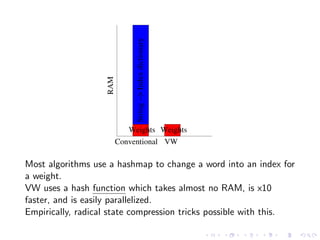
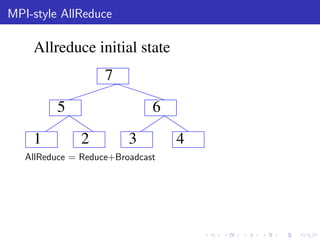
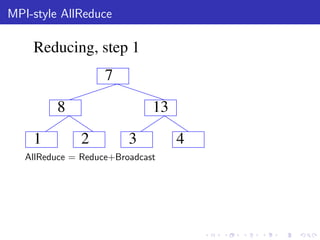
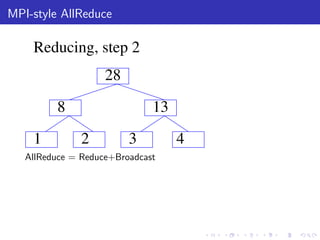
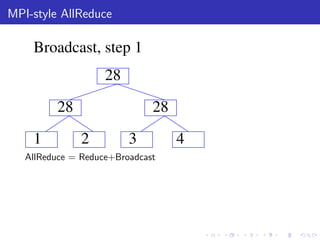
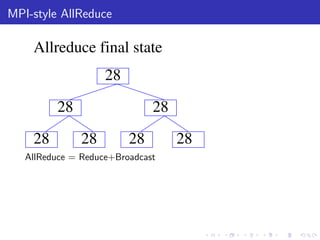
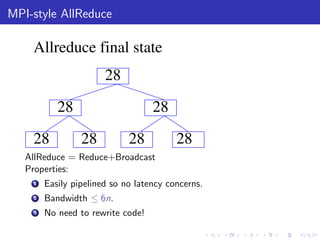
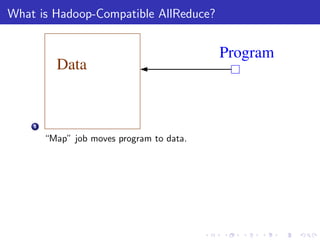
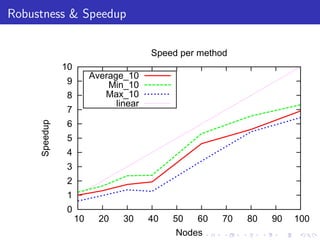
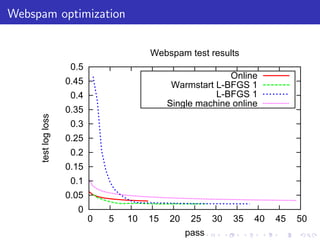
The document describes a terascale learning algorithm for training linear models on large datasets using distributed computing. It discusses using a hashing trick to reduce input complexity, an adaptive online gradient descent algorithm to warm-start L-BFGS batch optimization, and a custom all-reduce implementation to synchronize model parameters across nodes. The approach leverages Hadoop for fault tolerance while training linear models on up to 2.1 trillion features and 17 billion examples in 70 minutes, significantly faster than single machine algorithms.

1. A Terascale Learning Algorithm
Alekh Agarwal, Olivier Chapelle, Miroslav Dudik, and John
Langford
... And the Vowpal Wabbit project.

2. Applying for a fellowship in 1997

3. Applying for a fellowship in 1997
Interviewer: So, what do you want to do?

4. Applying for a fellowship in 1997
Interviewer: So, what do you want to do?
John: I’d like to solve AI.

5. Applying for a fellowship in 1997
Interviewer: So, what do you want to do?
John: I’d like to solve AI.
I: How?

6. Applying for a fellowship in 1997
Interviewer: So, what do you want to do?
John: I’d like to solve AI.
I: How?
J: I want to use parallel learning algorithms to create fantastic
learning machines!

7. Applying for a fellowship in 1997
Interviewer: So, what do you want to do?
John: I’d like to solve AI.
I: How?
J: I want to use parallel learning algorithms to create fantastic
learning machines!
I: You fool! The only thing parallel machines are good for is
computational windtunnels!

8. Applying for a fellowship in 1997
Interviewer: So, what do you want to do?
John: I’d like to solve AI.
I: How?
J: I want to use parallel learning algorithms to create fantastic
learning machines!
I: You fool! The only thing parallel machines are good for is
computational windtunnels!
The worst part: he had a point. At that time, smarter learning
algorithms always won. To win, we must master the best
single-machine learning algorithms, then clearly beat them with a
parallel approach.

9. Demonstration

10. Terascale Linear Learning ACDL11
Given 2.1 Terafeatures of data, how can you learn a good linear
predictor fw (x) = i wi xi ?

11. Terascale Linear Learning ACDL11
Given 2.1 Terafeatures of data, how can you learn a good linear
predictor fw (x) = i wi xi ?
2.1T sparse features
17B Examples
16M parameters
1K nodes

12. Terascale Linear Learning ACDL11
Given 2.1 Terafeatures of data, how can you learn a good linear
predictor fw (x) = i wi xi ?
2.1T sparse features
17B Examples
16M parameters
1K nodes
70 minutes = 500M features/second: faster than the IO
bandwidth of a single machine⇒ we beat all possible single
machine linear learning algorithms.

13. Terascale Linear Learning ACDL11
Given 2.1 Terafeatures of data, how can you learn a good linear
predictor fw (x) = i wi xi ?
2.1T sparse features
17B Examples
16M parameters
1K nodes
70 minutes = 500M features/second: faster than the IO
bandwidth of a single machine⇒ we beat all possible single
machine linear learning algorithms.
(Actually, we can do even better now.)

14. book
Features/s
100
1000
10000
100000
1e+06
1e+07
1e+08
1e+09
RBF-SVM
MPI?-500
RCV1
Ensemble Tree
MPI-128
Synthetic
single
parallel
RBF-SVM
TCP-48
MNIST 220K
Decision Tree
MapRed-200
Ad-Bounce #
Boosted DT
MPI-32
Speed per method
Ranking #
Linear
Threads-2
RCV1
Linear
Hadoop+TCP-1000
Ads *&
Compare: Other Supervised Algorithms in Parallel Learning

15. The tricks we use
First Vowpal Wabbit Newer Algorithmics Parallel Stuff
Feature Caching Adaptive Learning Parameter Averaging
Feature Hashing Importance Updates Smart Averaging
Online Learning Dimensional Correction Gradient Summing
L-BFGS Hadoop AllReduce
Hybrid Learning
We’ll discuss Hashing, AllReduce, then how to learn.

16. String −> Index dictionary
RAM
Weights Weights
Conventional VW
Most algorithms use a hashmap to change a word into an index for
a weight.
VW uses a hash function which takes almost no RAM, is x10
faster, and is easily parallelized.
Empirically, radical state compression tricks possible with this.

17. MPI-style AllReduce
Allreduce initial state
7
5 6
1 2 3 4
AllReduce = Reduce+Broadcast

18. MPI-style AllReduce
Reducing, step 1
7
8 13
1 2 3 4
AllReduce = Reduce+Broadcast

19. MPI-style AllReduce
Reducing, step 2
28
8 13
1 2 3 4
AllReduce = Reduce+Broadcast

20. MPI-style AllReduce
Broadcast, step 1
28
28 28
1 2 3 4
AllReduce = Reduce+Broadcast

21. MPI-style AllReduce
Allreduce final state
28
28 28
28 28 28 28
AllReduce = Reduce+Broadcast

22. MPI-style AllReduce
Allreduce final state
28
28 28
28 28 28 28
AllReduce = Reduce+Broadcast
Properties:
1 Easily pipelined so no latency concerns.
2 Bandwidth ≤ 6n.
3 No need to rewrite code!

23. An Example Algorithm: Weight averaging
n = AllReduce(1)
While (pass number < max)
1 While (examples left)
1 Do online update.
2 AllReduce(weights)
3 For each weight w ← w /n

24. An Example Algorithm: Weight averaging
n = AllReduce(1)
While (pass number < max)
1 While (examples left)
1 Do online update.
2 AllReduce(weights)
3 For each weight w ← w /n
Other algorithms implemented:
1 Nonuniform averaging for online learning
2 Conjugate Gradient
3 LBFGS

25. What is Hadoop-Compatible AllReduce?
Program
Data
1
“Map” job moves program to data.

26. What is Hadoop-Compatible AllReduce?
Program
Data
1
“Map” job moves program to data.
2 Delayed initialization: Most failures are disk failures. First
read (and cache) all data, before initializing allreduce. Failures
autorestart on different node with identical data.

27. What is Hadoop-Compatible AllReduce?
Program
Data
1
“Map” job moves program to data.
2 Delayed initialization: Most failures are disk failures. First
read (and cache) all data, before initializing allreduce. Failures
autorestart on different node with identical data.
3 Speculative execution: In a busy cluster, one node is often
slow. Hadoop can speculatively start additional mappers. We
use the first to finish reading all data once.

28. What is Hadoop-Compatible AllReduce?
Program
Data
1
“Map” job moves program to data.
2 Delayed initialization: Most failures are disk failures. First
read (and cache) all data, before initializing allreduce. Failures
autorestart on different node with identical data.
3 Speculative execution: In a busy cluster, one node is often
slow. Hadoop can speculatively start additional mappers. We
use the first to finish reading all data once.
The net effect: Reliable execution out to perhaps 10K node-hours.

29. Algorithms: Preliminaries
Optimize so few data passes required ⇒ Smart algorithms.
Basic problem with gradient descent = confused units.
fw (x) = i wi xi
(x)−y 2
⇒ ∂(fw ∂wi ) = 2(fw (x) − y )xi which has units of i.
But wi naturally has units of 1/i since doubling xi implies halving
wi to get the same prediction.
Crude fixes:
∂ 2 −1
1 Newton: Multiply inverse Hessian: ∂wi ∂wj by gradient to
get update direction.
2 Normalize update so total step size is controlled.

30. Algorithms: Preliminaries
Optimize so few data passes required ⇒ Smart algorithms.
Basic problem with gradient descent = confused units.
fw (x) = i wi xi
(x)−y 2
⇒ ∂(fw ∂wi ) = 2(fw (x) − y )xi which has units of i.
But wi naturally has units of 1/i since doubling xi implies halving
wi to get the same prediction.
Crude fixes:
2 −1
1 Newton: Multiply inverse Hessian: ∂w∂∂wj
i
by gradient to
get update direction...but computational complexity kills you.
2 Normalize update so total step size is controlled...but this just
works globally rather than per dimension.

31. Approach Used
1 Optimize hard so few data passes required.
1 L-BFGS = batch algorithm that builds up approximate inverse
∆ ∆T
hessian according to: ∆w ∆w where ∆w is a change in weights
T
w g
w and ∆g is a change in the loss gradient g .

32. Approach Used
1 Optimize hard so few data passes required.
1 L-BFGS = batch algorithm that builds up approximate inverse
∆ ∆T
hessian according to: ∆w ∆w where ∆w is a change in weights
T
w g
w and ∆g is a change in the loss gradient g .
2 Dimensionally correct, adaptive, online, gradient descent for
small-multiple passes.
1 Online = update weights after seeing each example.
1
2 Adaptive = learning rate of feature i according to √P
gi2
where gi = previous gradients.
3 Dimensionally correct = still works if you double all feature
values.
3 Use (2) to warmstart (1).

33. Approach Used
1 Optimize hard so few data passes required.
1 L-BFGS = batch algorithm that builds up approximate inverse
∆ ∆T
hessian according to: ∆w ∆w where ∆w is a change in weights
T
w g
w and ∆g is a change in the loss gradient g .
2 Dimensionally correct, adaptive, online, gradient descent for
small-multiple passes.
1 Online = update weights after seeing each example.
1
2 Adaptive = learning rate of feature i according to √P
gi2
where gi = previous gradients.
3 Dimensionally correct = still works if you double all feature
values.
3 Use (2) to warmstart (1).
2 Use map-only Hadoop for process control and error recovery.

34. Approach Used
1 Optimize hard so few data passes required.
1 L-BFGS = batch algorithm that builds up approximate inverse
∆ ∆T
hessian according to: ∆w ∆w where ∆w is a change in weights
T
w g
w and ∆g is a change in the loss gradient g .
2 Dimensionally correct, adaptive, online, gradient descent for
small-multiple passes.
1 Online = update weights after seeing each example.
1
2 Adaptive = learning rate of feature i according to √P
gi2
where gi = previous gradients.
3 Dimensionally correct = still works if you double all feature
values.
3 Use (2) to warmstart (1).
2 Use map-only Hadoop for process control and error recovery.
3 Use custom AllReduce code to sync state.

35. Approach Used
1 Optimize hard so few data passes required.
1 L-BFGS = batch algorithm that builds up approximate inverse
∆ ∆T
hessian according to: ∆w ∆w where ∆w is a change in weights
T
w g
w and ∆g is a change in the loss gradient g .
2 Dimensionally correct, adaptive, online, gradient descent for
small-multiple passes.
1 Online = update weights after seeing each example.
1
2 Adaptive = learning rate of feature i according to √P
gi2
where gi = previous gradients.
3 Dimensionally correct = still works if you double all feature
values.
3 Use (2) to warmstart (1).
2 Use map-only Hadoop for process control and error recovery.
3 Use custom AllReduce code to sync state.
4 Always save input examples in a cachefile to speed later
passes.

36. Approach Used
1 Optimize hard so few data passes required.
1 L-BFGS = batch algorithm that builds up approximate inverse
∆ ∆T
hessian according to: ∆w ∆w where ∆w is a change in weights
T
w g
w and ∆g is a change in the loss gradient g .
2 Dimensionally correct, adaptive, online, gradient descent for
small-multiple passes.
1 Online = update weights after seeing each example.
1
2 Adaptive = learning rate of feature i according to √P
gi2
where gi = previous gradients.
3 Dimensionally correct = still works if you double all feature
values.
3 Use (2) to warmstart (1).
2 Use map-only Hadoop for process control and error recovery.
3 Use custom AllReduce code to sync state.
4 Always save input examples in a cachefile to speed later
passes.
5 Use hashing trick to reduce input complexity.

37. Approach Used
1 Optimize hard so few data passes required.
1 L-BFGS = batch algorithm that builds up approximate inverse
∆ ∆T
hessian according to: ∆w ∆w where ∆w is a change in weights
T
w g
w and ∆g is a change in the loss gradient g .
2 Dimensionally correct, adaptive, online, gradient descent for
small-multiple passes.
1 Online = update weights after seeing each example.
1
2 Adaptive = learning rate of feature i according to √P
gi2
where gi = previous gradients.
3 Dimensionally correct = still works if you double all feature
values.
3 Use (2) to warmstart (1).
2 Use map-only Hadoop for process control and error recovery.
3 Use custom AllReduce code to sync state.
4 Always save input examples in a cachefile to speed later
passes.
5 Use hashing trick to reduce input complexity.
Open source in Vowpal Wabbit 6.0. Search for it.

38. Robustness & Speedup
Speed per method
10
Average_10
9 Min_10
8 Max_10
linear
7
Speedup
6
5
4
3
2
1
0
10 20 30 40 50 60 70 80 90 100
Nodes

39. Webspam optimization
Webspam test results
0.5
Online
0.45 Warmstart L-BFGS 1
0.4 L-BFGS 1
Single machine online
0.35
test log loss
0.3
0.25
0.2
0.15
0.1
0.05
0
0 5 10 15 20 25 30 35 40 45 50
pass

40. How does it work?
The launch sequence (on Hadoop):
1 mapscript.sh hdfs output hdfs input maps asked
2 mapscript.sh starts spanning tree on the gateway. Each vw
connects to spanning tree to learn which other vw is adjacent
in the binary tree.
3 mapscript.sh starts hadoop streaming map-only job: runvw.sh
4 runvw.sh calls vw twice.
5 First vw call does online learning while saving examples in a
cachefile. Weights are averaged before saving.
6 Second vw uses online solution to warmstart L-BFGS.
Gradients are shared via allreduce.
Example: mapscript.sh outdir indir 100
Everything also works in a nonHadoop cluster: you just need to
script more to do some of the things that Hadoop does for you.

41. How does this compare to other cluster learning efforts?
Mahout was founded as the MapReduce ML project, but has
grown to include VW-style online linear learning. For linear
learning, VW is superior:
1 Vastly faster.
2 Smarter Algorithms.
Other algorithms exist in Mahout, but they are apparently buggy.
AllReduce seems a superior paradigm in the 10K node-hours
regime for Machine Learning.
Graphlab(@CMU) doesn’t overlap much. This is mostly about
graphical model evaluation and learning.
Ultra LDA(@Y!), overlaps partially. VW has noncluster-parallel
LDA which is perhaps x3 more effecient.

42. Can allreduce be used by others?
It might be incorporated directly into next generation Hadoop.
But for now, it’s quite easy to use the existing code.
void all reduce(char* buffer, int n, std::string master location,
size t unique id, size t total, size t node);
buffer = pointer to some floats
n = number of bytes (4*floats)
master location = IP address of gateway
unique id = nonce (unique for different jobs)
total = total number of nodes
node = node id number
The call is stateful: it initializes the topology if necessary.

43. Further Pointers
search://Vowpal Wabbit
mailing list: vowpal wabbit@yahoogroups.com
VW tutorial (Preparallel): http://videolectures.net
Machine Learning (Theory) blog: http://hunch.net

44. Bibliography: Original VW
Caching L. Bottou. Stochastic Gradient Descent Examples on Toy
Problems, http://leon.bottou.org/projects/sgd, 2007.
Release Vowpal Wabbit open source project,
http://github.com/JohnLangford/vowpal_wabbit/wiki,
2007.
Hashing Q. Shi, J. Petterson, G. Dror, J. Langford, A. Smola, and
SVN Vishwanathan, Hash Kernels for Structured Data,
AISTAT 2009.
Hashing K. Weinberger, A. Dasgupta, J. Langford, A. Smola, and J.
Attenberg, Feature Hashing for Large Scale Multitask
Learning, ICML 2009.

45. Bibliography: Algorithmics
L-BFGS J. Nocedal, Updating Quasi-Newton Matrices with Limited
Storage, Mathematics of Computation 35:773–782, 1980.
Adaptive H. B. McMahan and M. Streeter, Adaptive Bound
Optimization for Online Convex Optimization, COLT 2010.
Adaptive J. Duchi, E. Hazan, and Y. Singer, Adaptive Subgradient
Methods for Online Learning and Stochastic Optimization,
COLT 2010.
Import. N. Karampatziakis, and J. Langford, Online Importance
Weight Aware Updates, UAI 2011.

46. Bibliography: Parallel
grad sum C. Teo, Q. Le, A. Smola, V. Vishwanathan, A Scalable
Modular Convex Solver for Regularized Risk Minimization,
KDD 2007.
averaging G. Mann, R. Mcdonald, M. Mohri, N. Silberman, and D.
Walker. Efficient large-scale distributed training of conditional
maximum entropy models, NIPS 2009.
averaging K. Hall, S. Gilpin, and G. Mann, MapReduce/Bigtable for
Distributed Optimization, LCCC 2010.
(More forthcoming, of course)