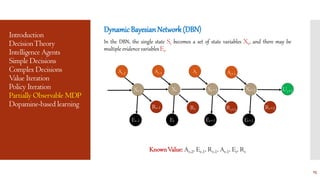
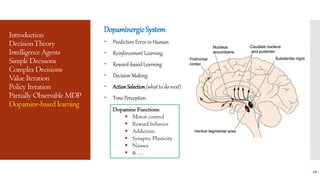
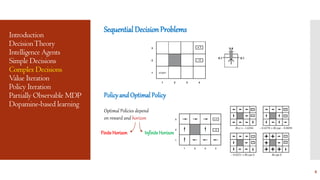
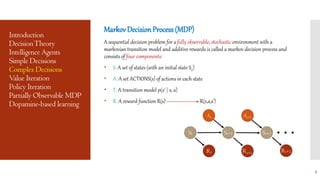
This document provides an overview of Markov Decision Processes (MDPs) and related concepts in decision theory and reinforcement learning. It defines MDPs and their components, describes algorithms for solving MDPs like value iteration and policy iteration, and discusses extensions to partially observable MDPs. It also briefly mentions dynamic Bayesian networks, the dopaminergic system, and its role in reinforcement learning and decision making.




![Introduction
DecisionTheory
Intelligence Agents
Simple Decisions
Complex Decisions
Value Iteration
Policy Iteration
Partially Observable MDP
Dopamine-based learning
MaximumExpectedUtility (MEU)
A rational agent should choose the action that maximizes the agent’s expected utility:
action = argmaxa EU(a|e)
EU(a|e) = ∑P(RESULT(a)= s’ | a, e) U(s’)
The Value of Information
VPI (Ej) = [∑P(Ej = ejk | e) EU (aejk
| e, Ej = ejk)] − EU (a|e)
5
Random VariableNondeterministic Partially Observable Environments](https://image.slidesharecdn.com/markovdecisionprocess-180925102304/85/Markov-decision-process-5-320.jpg)

![Introduction
DecisionTheory
Intelligence Agents
Simple Decisions
Complex Decisions
Value Iteration
Policy Iteration
Partially Observable MDP
Dopamine-based learning
Utilities of Sequences
1. Additive rewards:
Uh([s0, s1, s2, . . .]) = R(s0) + R(s1) + R(s2) + · · ·
2. Discounted rewards:
Uh([s0, s1, s2, . . .]) = R(s0) + γR(s1) + γ2R(s2) + · · ·
With discounted rewards, the utility of an infinite sequence is finite. (γ < 1)
Uh([s0, s1, s2, . . .]) = ∑γtR(st) ≤ ∑γtRmax = Rmax/(1 − γ)
9
Discount Factor is a number between 0 and 1](https://image.slidesharecdn.com/markovdecisionprocess-180925102304/85/Markov-decision-process-9-320.jpg)
![Introduction
DecisionTheory
Intelligence Agents
Simple Decisions
Complex Decisions
Value Iteration
Policy Iteration
Partially Observable MDP
Dopamine-based learning
The Bellman Equationfor Utilities
The utility of a state is the immediate reward for that state plus the expected discounted
utility of the next state, assuming that the agent chooses the optimal action.
U’(s) = R(s) + γ maxa∈A(s) [∑P(s’ | s, a)U(s’)]
The Value IterationAlgorithm
10](https://image.slidesharecdn.com/markovdecisionprocess-180925102304/85/Markov-decision-process-10-320.jpg)