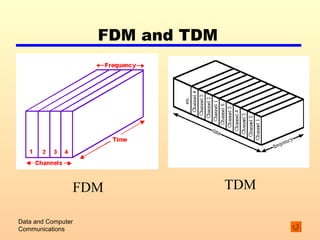
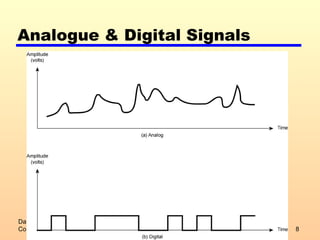
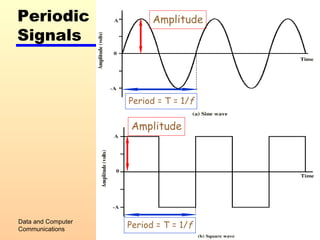
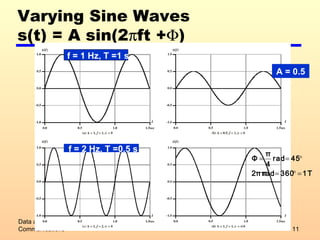
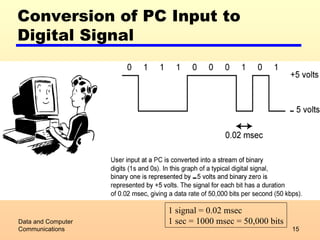
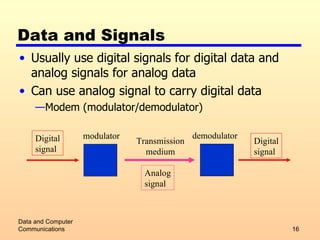
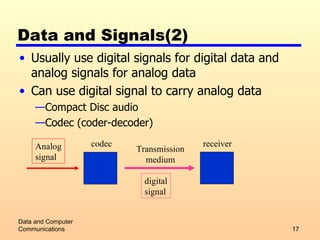
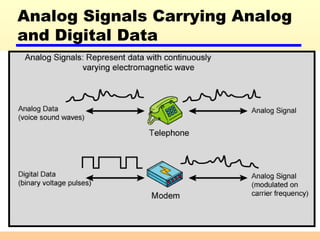
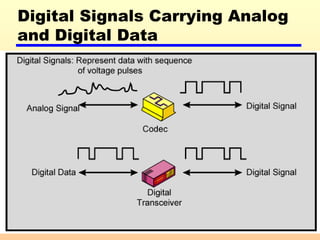
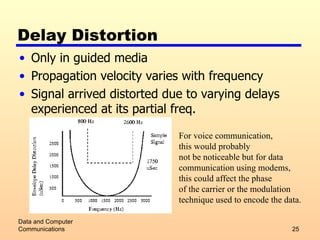
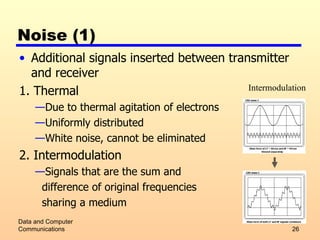
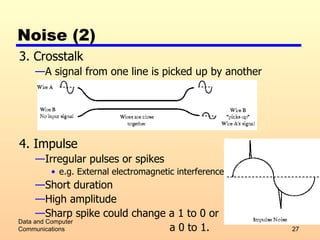
The document introduces some key concepts in data communication, including: 1) Different types of transmission media such as guided (e.g. fiber optic cable) and unguided (e.g. wireless). 2) Analog and digital signals and how analog data can be transmitted using either type of signal. 3) Factors that can impair transmission such as attenuation, delay distortion, and different types of noise. The Nyquist bandwidth and Shannon capacity formulas for calculating maximum data rates are also covered.

1. Chapter 2 Data Communication 2.1 Data Transmission Key Points

2. Terminology (1) Introduction of some concepts & terms used. Transmitter Receiver Medium Com. in form of electromagnetic waves Guided medium Along a physical path e.g. twisted pair, optical fiber Unguided medium Means for transmitting electromagnetic waves but not guide them e.g. air, water, vacuum Data and Computer Communications

3. Terminology (2) Direct link No intermediate devices Transmission path between 2 devices Can apply to both guided & unguided media Point-to-point Direct link Only 2 devices share link Multi-point More than two devices share the link Data and Computer Communications

4. Terminology (3) Transmission mode : Simplex One direction e.g. Television Half duplex Either direction, but only one way at a time e.g. police radio Full duplex Both directions at the same time e.g. telephone Data and Computer Communications

5. Frequency Time domain concepts Analog signal Various in a smooth way over time Digital signal Maintains a constant level then changes to another constant level Periodic signal Pattern repeated over time Aperiodic signal Pattern not repeated over time Data and Computer Communications

6. Analog and Digital Data Transmission Data Entities that convey meaning or info Signals Electric or electromagnetic representations of data Transmission Communication of data by propagation and processing of signals Data and Computer Communications

7. Analog and Digital Data Analog Continuous values within some interval e.g. sound, video Digital Discrete values e.g. text, integers Data and Computer Communications

8. Analogue & Digital Signals Data and Computer Communications

9. Periodic Signals Data and Computer Communications Amplitude Period = T = 1/ f Period = T = 1/ f Amplitude

10. Sine Wave Fundamental periodic signal Peak Amplitude (A) maximum strength of signal volts Frequency (f) Rate of change of signal Hertz (Hz) or cycles per second Period = time for one repetition (T) T = 1/f Phase (  ) Relative position in time Data and Computer Communications

11. Varying Sine Waves s(t) = A sin(2  ft +  ) Data and Computer Communications A = 0.5 f = 1 Hz, T =1 s f = 2 Hz, T =0.5 s

12. Components of Speech Frequency range (of hearing) 20Hz-20kHz Speech 100Hz-7kHz Easily converted into electromagnetic signal for transmission Sound frequencies with varying volume converted into electromagnetic frequencies with varying voltage Limit frequency range for voice channel 300-3400Hz Data and Computer Communications

13. Conversion of Voice Input into Analog Signal Data and Computer Communications

14. Binary Digital Data Generated by computer terminals etc. Converted into digital voltage pulses for transmission Two dc components Voltage levels – 1s and 0s Bandwidth of signal depends on data rate Bandwidth approximation of digital pulse stream Data and Computer Communications

15. Conversion of PC Input to Digital Signal Data and Computer Communications - - 1 signal = 0.02 msec 1 sec = 1000 msec = 50,000 bits

16. Data and Signals Usually use digital signals for digital data and analog signals for analog data Can use analog signal to carry digital data Modem (modulator/demodulator) Data and Computer Communications Digital signal modulator Analog signal demodulator Digital signal Transmission medium

17. Data and Signals(2) Usually use digital signals for digital data and analog signals for analog data Can use digital signal to carry analog data Compact Disc audio Codec (coder-decoder) Data and Computer Communications Analog signal codec digital signal receiver Transmission medium

18. Analog Signals Carrying Analog and Digital Data Data and Computer Communications

19. Digital Signals Carrying Analog and Digital Data Data and Computer Communications

20. Analog Transmission Analog signal transmitted without regard to content May be analog or digital data Eg: Analog data: voice, Digital data: binary data that passed through a modem Attenuated over distance Use amplifiers to boost signal Also amplifies noise Disadvantage: distance distortion Analog data (eg. voice) :distortion can be tolerated Digital data :introduce errors Data and Computer Communications

21. Digital Transmission Concerned with content(binary) Integrity endangered by noise, attenuation etc. -limited distance Repeaters used Repeater receives digital signal Extracts bit pattern recover the patterns of 1s and 0s Retransmits a new signal Attenuation is overcome Noise is not amplified Data and Computer Communications

22. Advantages of Digital Transmission Digital technology Low cost LSI/VLSI technology Data integrity Longer distances over lower quality lines with the use of repeater(regenerate) rather than amplifier Capacity utilization High bandwidth links economical. eg: satellite channels, optical fiber High degree of multiplexing easier with digital techniques Time division multiplexing (TDM) rather than frequency division multiplexing (FDM) Security & Privacy Encryption To digital data and analog data that have been digitized Integration Can treat analog and digital data similarly Data and Computer Communications

23. Transmission Impairments Signal received may differ from signal transmitted Analog - degradation of signal quality Digital - bit errors Caused by Attenuation and attenuation distortion Delay distortion Noise Data and Computer Communications

24. Attenuation Signal strength falls off with distance Depends on medium Received signal strength: must be enough to be detected must be sufficiently higher than noise to be received without error Can be deal by using amplifier/repeater Attenuation is an increasing function of frequency Noticeable for analog signal Use equalizer to smooth out attenuation effect Use amplifier to amplify high freq. more than low freq. Data and Computer Communications

25. Delay Distortion Only in guided media Propagation velocity varies with frequency Signal arrived distorted due to varying delays experienced at its partial freq. Data and Computer Communications For voice communication, this would probably not be noticeable but for data communication using modems, this could affect the phase of the carrier or the modulation technique used to encode the data.

26. Noise (1) Additional signals inserted between transmitter and receiver 1. Thermal Due to thermal agitation of electrons Uniformly distributed White noise, cannot be eliminated 2. Intermodulation Signals that are the sum and difference of original frequencies sharing a medium Data and Computer Communications Intermodulation

27. Noise (2) 3. Crosstalk A signal from one line is picked up by another 4. Impulse Irregular pulses or spikes e.g. External electromagnetic interference Short duration High amplitude Sharp spike could change a 1 to 0 or a 0 to 1. Data and Computer Communications

28. Thermal Noise The amount of thermal,noise to e found in a bandiwdth of 1 Hz in any device or conductor is: N 0 = kT (W/Hz) N 0 = noise power density in watt per 1 Hz of bandwidth k = boltzman constant = 1.38 x 10 T = temp, in Kelvins Thermal noise in watt present in a bandwidth of B N = kTB = 10 log k + 10 log T + 10 log B Data and Computer Communications

29. Channel Capacity Def. :Max. rate at which data can be transmitted over a given com. path/channel under given condition Concept of channel capacity: Data rate In bits per second Rate at which data can be communicated Bandwidth Range of frequency In cycles per second or Hertz, (unit for frequency, f= 1/T) Constrained by transmitter and medium Data and Computer Communications

30. Channel Capacity (cont) Noise Average level of noise over com. path Error rate Rate at which errors occur Reception of a 1 when 0 was transmitted or the other way Com. facilities are expensive Bandwidth cost Make efficient use of given bandwidth Main constraint in achieving this efficiency is noise Data and Computer Communications

31. Nyquist Bandwidth In the case of a channel that is noise free, limitation on data rate is simply the bandwidth of the signal. If rate of signal transmission is 2 B then signal with frequencies no greater than B is sufficient to carry signal rate Given bandwidth B, highest signal rate is 2B Given binary signal, data rate supported by B Hz is 2B bps Can be increased by using M signal levels C= 2 B log 2 M Data and Computer Communications C = Channel capacity

32. Nyquist Bandwidth (2) Can be increased by using M signal levels C= 2 B log 2 M M is the number of discrete signal or voltage levels Eg: 1 bit value (0 to 1) = 2 1 (M= 2 levels) 2 bit value (00 to 11) =2 2 (M= 4 levels) 3 bit value (000 to 111) =2 3 (M= 8 levels) Data and Computer Communications

33. Nyquist Bandwidth (3) Nyquist’s formula : C= 2 B log 2 M Ex. 1: Consider a voice channel being used to transmit digital data. Assume a bandwidth of 3100 Hz. So the data rate, C of the channel is 2 B = 6200bps For M= 8 (2 3 :bit value from 000 to 111), C becomes 18,600 bps for a bandwidth of 3100 Hz. Data and Computer Communications

34. Nyquist Bandwidth (4) Nyquist’s formula : C= 2 B log 2 M Ex. 2: For sampling rate for analog  digital signal. What data rate is needed for a signal with a bandwidth of 10,000Hz (1,000 to 11,000 Hz)? Solution: The sampling rate must be twice the highest frequency in the signal: Data rate = 2(11,000)=22,000 data/sec Data and Computer Communications

35. Shannon Capacity Formula Nyquist’s formula indicates that doubling the bandwidth doubles the data rate. Consider data rate, noise and error rate Faster data rate shortens each bit, so burst of noise affects more bits At given noise level, high data rate means higher error rate Greater signal strength would improve ability to receive data correctly in the presence of noise. Data and Computer Communications

36. Shannon Capacity Formula (2) Formula developed by a mathematician Claude Shannon. Signal to noise ratio (in decibels) SNR db = 10 log 10 (signal/noise) Ex.: Suppose that V s = 10.0 μ v and V n = 1.00 μ v . Then S/N = 20 log(10(1.00)) = 20.0 dB Max. channel capacity C=B log 2 (1+SNR) This is error free capacity Data and Computer Communications

37. Shannon Capacity Formula (3) Ex.2: Consider an extremely noisy channel in which the value of the signal-to-noise ration is almost zero. In other words, the noise is so strong that the signal is faint. For this channel, the capacity is calculated as C = B log 2 (1 + S/N) = B log 2 (1 + 0) = B log 2 (1) = B x 0 = 0 This means that the capacity of this channel is zero regardless of the bandwidth. In other words, we cannot send any data through this channel. Data and Computer Communications

38. Shannon Capacity Formula (3) Let us consider an ex. that relates te Nyquist and Shannon formulations. Ex.: Suppose that the spectrum of a channel is between 3 MHz and 4 MHz and SNR dB =24 dB B = 4 MHz – 3 MHz = 1 MHz SNR dB = 24 dB = 10 log 10 (SNR)=251 Using Shannon’s formula, C = 10 6 x log 2 (1+251) ≈10 6 x 8 = 8 Mbps Data and Computer Communications

39. Shannon Capacity Formula (4) Based on Nyquist’s formula, how many signaling levels are required? B = 4 MHz – 3 MHz = 1 MHz Using Shannon’s formula, C = 10 6 x log 2 (1+251) ≈106 x 8 = 8 Mbps C = 2 B log 2 M 8 x 10 6 = 2 x (10 6 ) x log 2 M 4 = log 2 M M = 16 Data and Computer Communications END!!!

40. CONCLUSION Successful transmission of data depends principally on 2 factors Quality of the signal being transmitted Characters of the transmission medium Data and Computer Communications

41. Key Points All forms of info. can be represented by electromagnetic signals Analog or Digital signals can be used to convey info. The greater the bandwidth of the signal, the greater its info.-carrying capacity Data and Computer Communications

42. Key Points (2) Major problem in designing a com. facility is transmission impairment Attenuation, delay attenuation, noise (thermal noise, intermodulation noise, crosstalk, impulse noise) Designer of com. facility must deal with 4 factors Bandwidth of signal, data rate that is used for digital info., amount of noise & other impairments, and the level of error rate that is acceptable. Data and Computer Communications

43. The first integrated circuits contained only a few transistors. Called " Small-Scale Integration " ( SSI ), they used circuits containing transistors numbering in the tens. The next step in the development of integrated circuits, taken in the late 1960s, introduced devices which contained hundreds of transistors on each chip, called " Medium-Scale Integration " ( MSI ). They were attractive economically because while they cost little more to produce than SSI devices, they allowed more complex systems to be produced using smaller circuit boards, less assembly work (because of fewer separate components), and a number of other advantages. Further development, driven by the same economic factors, led to " Large-Scale Integration " ( LSI ) in the mid 1970s, with tens of thousands of transistors per chip. Integrated circuits such as 1K-bit RAMs, calculator chips, and the first microprocessors, that began to be manufactured in moderate quantities in the early 1970s, had under 4000 transistors. True LSI circuits, approaching 10,000 transistors, began to be produced around 1974, for computer main memories and second-generation microprocessors. The final step in the development process, starting in the 1980s and continuing on, was " Very Large-Scale Integration" (VLSI), with hundreds of thousands of transistors, and beyond (well past several million in the latest stages). For the first time it became possible to fabricate a CPU on a single integrated circuit, to create a microprocessor. LSI and VLSI Data and Computer Communications

44. FDM and TDM Data and Computer Communications FDM TDM