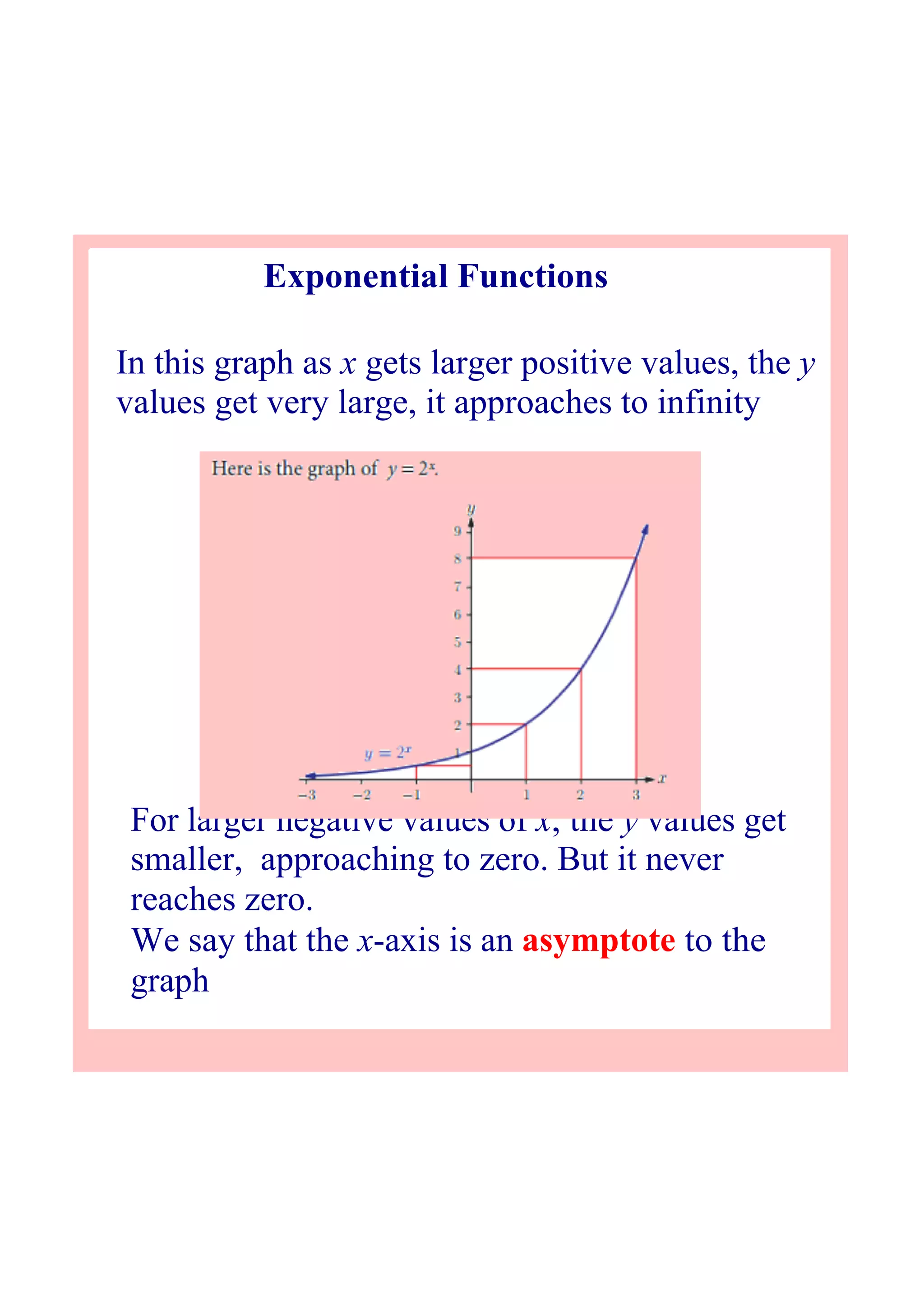
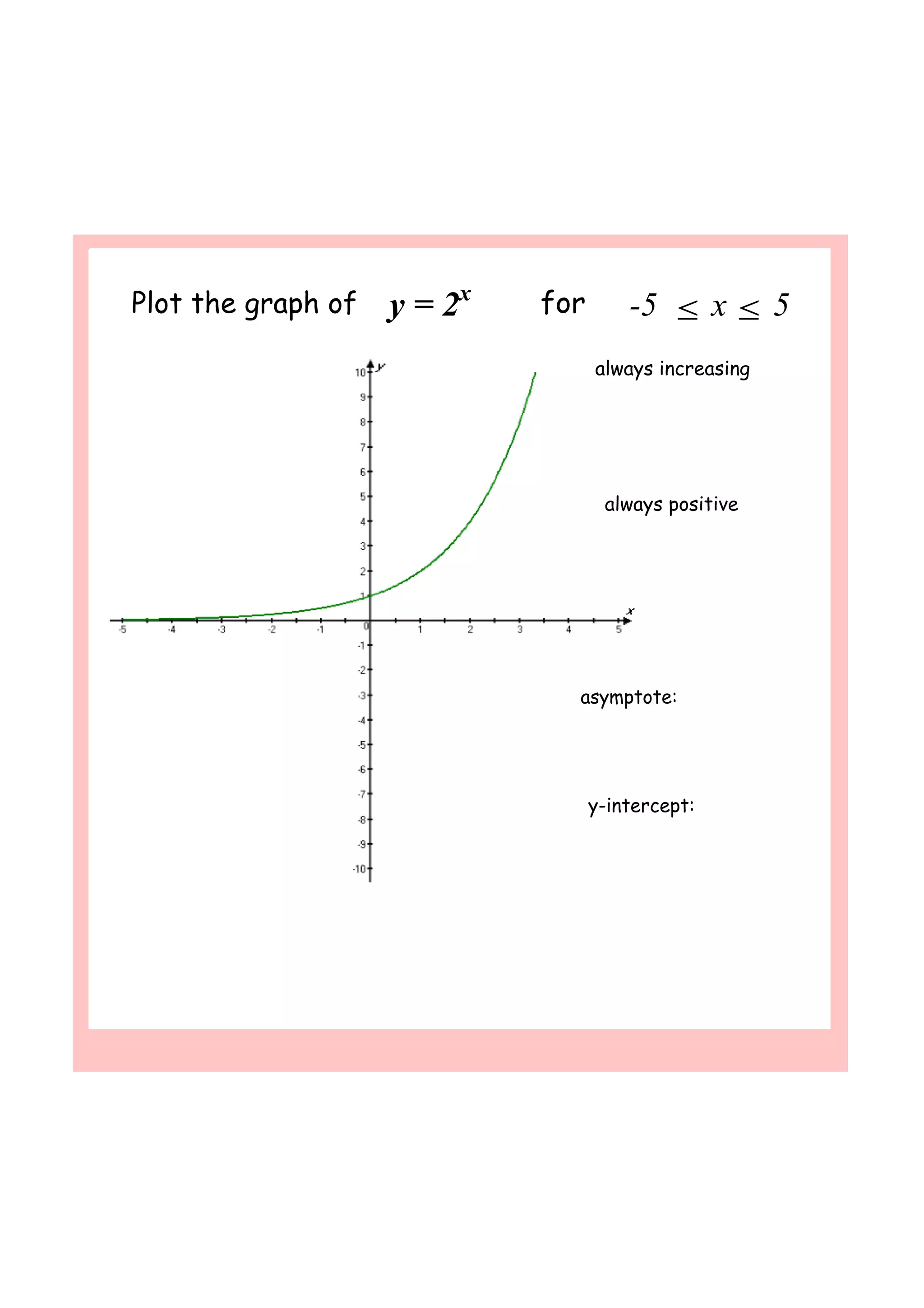
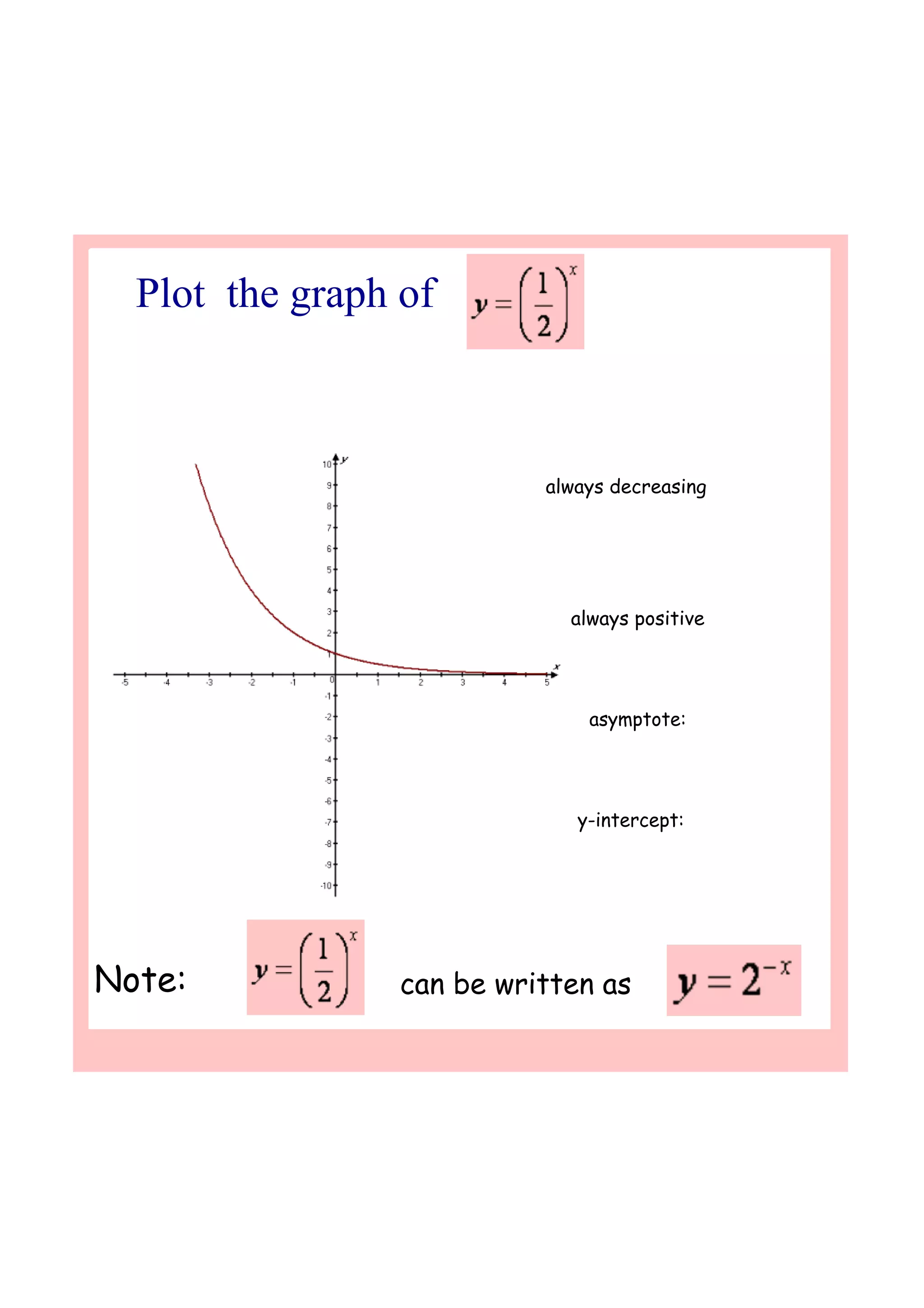
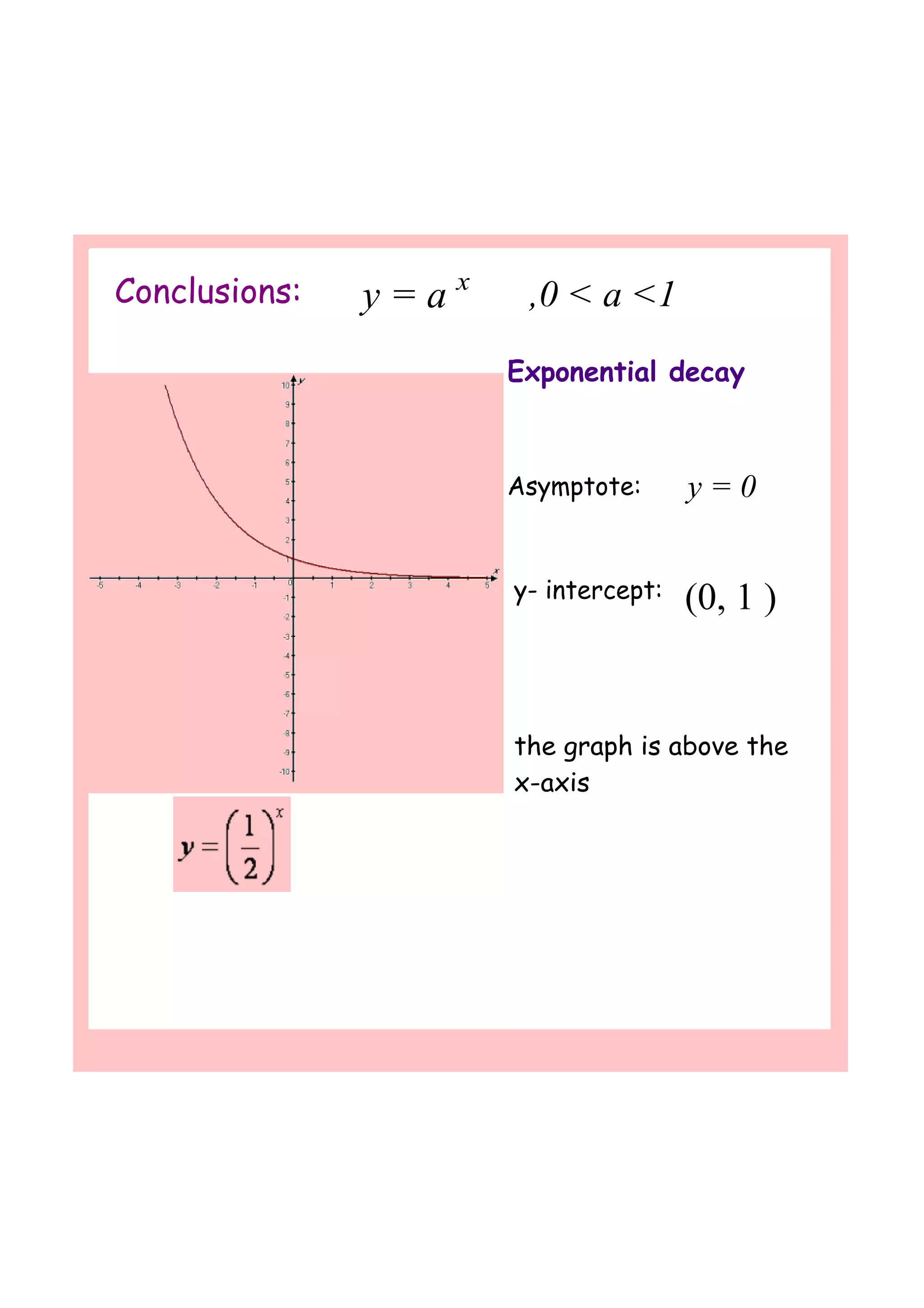
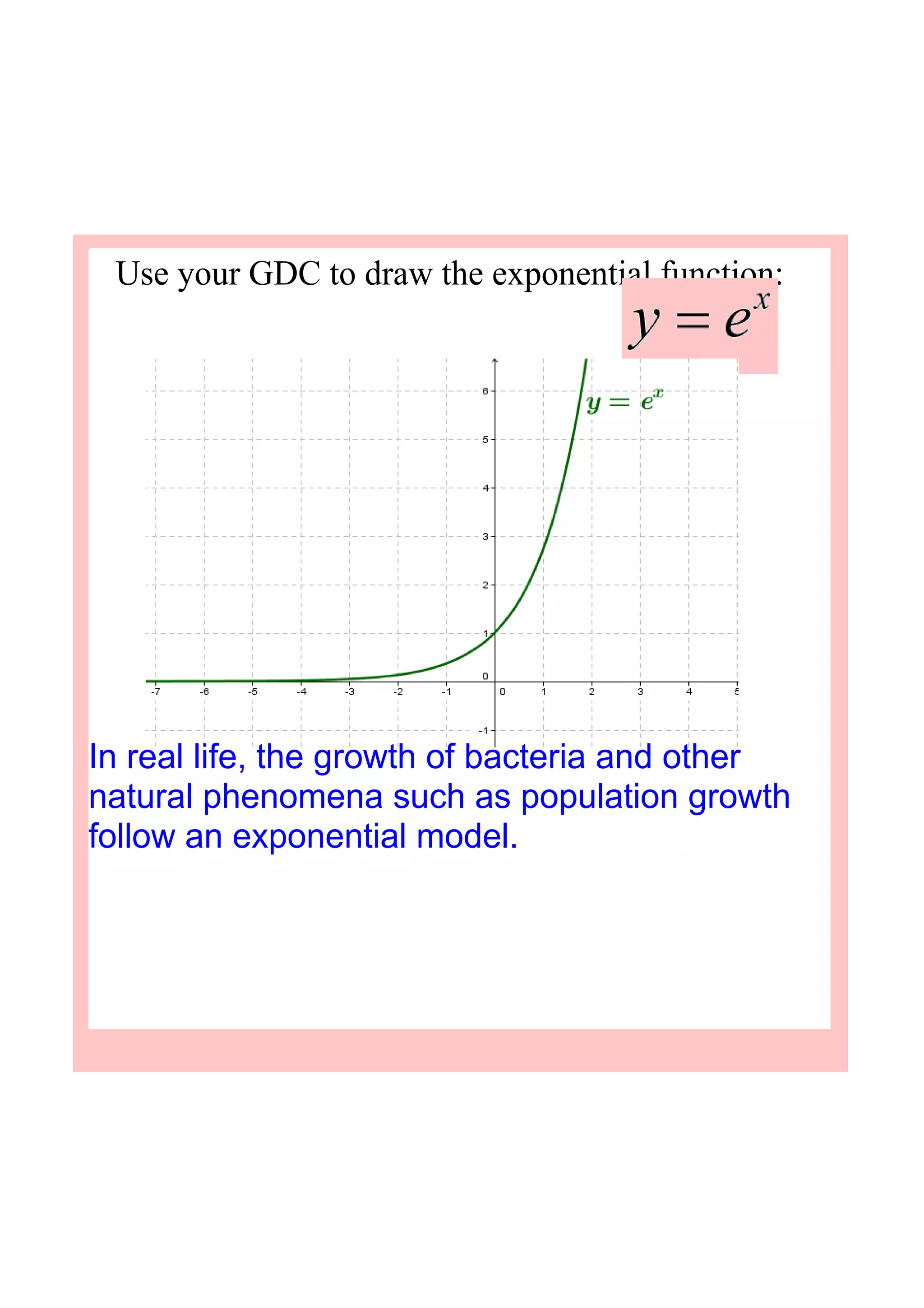
This document discusses exponential functions and their properties. It explores exponential growth and decay through graphs of functions like y=2^x and y=0.5^x. It shows that as x increases, exponential growth functions approach infinity, while decay functions approach zero. The document also introduces the irrational number e as the most important base for modeling continuous growth and decay. It shows how the function A=Ce^rt models continuous compound interest as the compounding period approaches infinity.

1. Exponential functions
To explore the properties of exponential functions and
their graphs.
To understand the nature and behavior of exponential
growth and decay.
To solve problems leading to exponential equations

2. Exponential Functions
In an exponential function the unknown appears
in the exponent like in:
f(x)= 2x

3. Plot the graph of y = 2x
for ­5 ≤ x ≤ 5

4. Exponential Functions
In this graph as x gets larger positive values, the y
values get very large, it approaches to infinity
For larger negative values of x, the y values get
smaller, approaching to zero. But it never
reaches zero.
We say that the x­axis is an asymptote to the
graph

5. Plot the graph of y = 2x
for ­5 ≤ x ≤ 5
always increasing
always positive
asymptote:
y-intercept:

6. On GDC explore the graphs of:
g (x) = 3 x
h(x) = 4 x
f (x) = 2 x
y=2xy=3xy=4x
y- intercept:
asymptote:

7. Plot the graph of
always decreasing
always positive
asymptote:
y-intercept:
Note: can be written as

8. Conclusions: y = a x
,a > 1
Exponential growth
Asymptote: y = 0
y- intercept: (0, 1 )
the graph is above the
x-axis
as in y = 2x

9. Conclusions: y = a x
,0 < a <1
Exponential decay
Asymptote: y = 0
y- intercept: (0, 1 )
the graph is above the
x-axis

10. Exponential functions can be used to model
real life situations as: growing of an investment,
of a tumor, of a population,etc.

11. The number of bacteria in a culture, N, is modelled
by the function: N = 1000 x 20.2t
, t≥ 0
where t is measured in days.
• Find the initial number of bacteria in the culture.
• Find the number of bacteria after 5 days.
• How long does it take for the number of bacteria
to grow to 4000?
1000
2000
10 days
• Use your GDC to plot the graph of N(t).

12. Mexico's population is increasing at a rate of
2 % per year. Calculate how long will it take for
Mexico's population to double.

13. In Nigeria the population is increasing at a rate of
6.2 % per year. Calculate how long will it take for
Nigeria's population to double.

14. The temperature T, in degrees Celsius, of a
cooling liquid is modelled by the equation:
T = 24 +72 (0.6)3t
where t is the time in minutes after the
cooling begins.
a) What is the initial temperature of the liquid?
b) Find the temperature of the liquid after 2 min.
c) How long does it take for the liquid to cool to
26o
C?
d) What temperature does the model predict the
liquid will eventually reach?

15. We have been working with examples of
exponential growth and decay and we used
different bases, bases like 10 and 2 are commonly
used for modelling certain applications. However
the most important base is an irrational number
denoted with the letter "e". ( e≈2.71828)

16. Do you remember the formula to calculate
compound interest?
A : future value
C: initial value
r: rate of interest
n : number of periods

17. we are going to study what happens when we
compound the interest continuously
we can write r as a decimal , then the formula will
be:

18. If we compound the interest twice a year the formula
will be:
To simplify this study, let's make r =1, C=1

19. If we compound the interest three times a year the
formula will be:
If we compound the interest twelve times a year the
formula will be:
we can continue to compound the interest daily,
minute­ly, second­ly...

20. Use the menu table in your calculator to
complete:
compounding n
annual
semi­annual
quaterly
monthly
daily
hourly
every minute
every second
1
2
4
12
365
8 760
525 600
31 536 000
2
2.25
2.4414...
2.613035...
2.714567...
2.718126...
2.71827921..
2.71828247..

21. Now move to the graph menu and plot the graph
of
we say that this function tends to number e

22. We say that the expression tends to e:
The irrational number e ( Euler's number)
http://torus.math.uiuc.edu/eggmath/Expon/numbere.html
http://abcnews.go.com/Technology/WhosCounting/story?id=99501&page=1

23. There are many real situations of continuous
change, to model them the most suitable function
is
Use your calculator to draw these functions.
continuous growth
continuous decay

24. Use your GDC to draw the exponential function:
In real life, the growth of bacteria and other
natural phenomena such as population growth
follow an exponential model.

25. Solve the equation:
But e is just a number, so it can be used as any
other
Use your calculator to find:
e2
2e ­ 1 e­2

26. Solve the equation:

27. Solve the equation:

28. Solve worksheet
exponential equations
Book page 48, Ex 2B and
page 51 Ex 2C
Exponential Equations and Functions 2014.docx

29. Attachments
Exponential Equations and Functions 2014.docx