Embed presentation
Downloaded 11 times

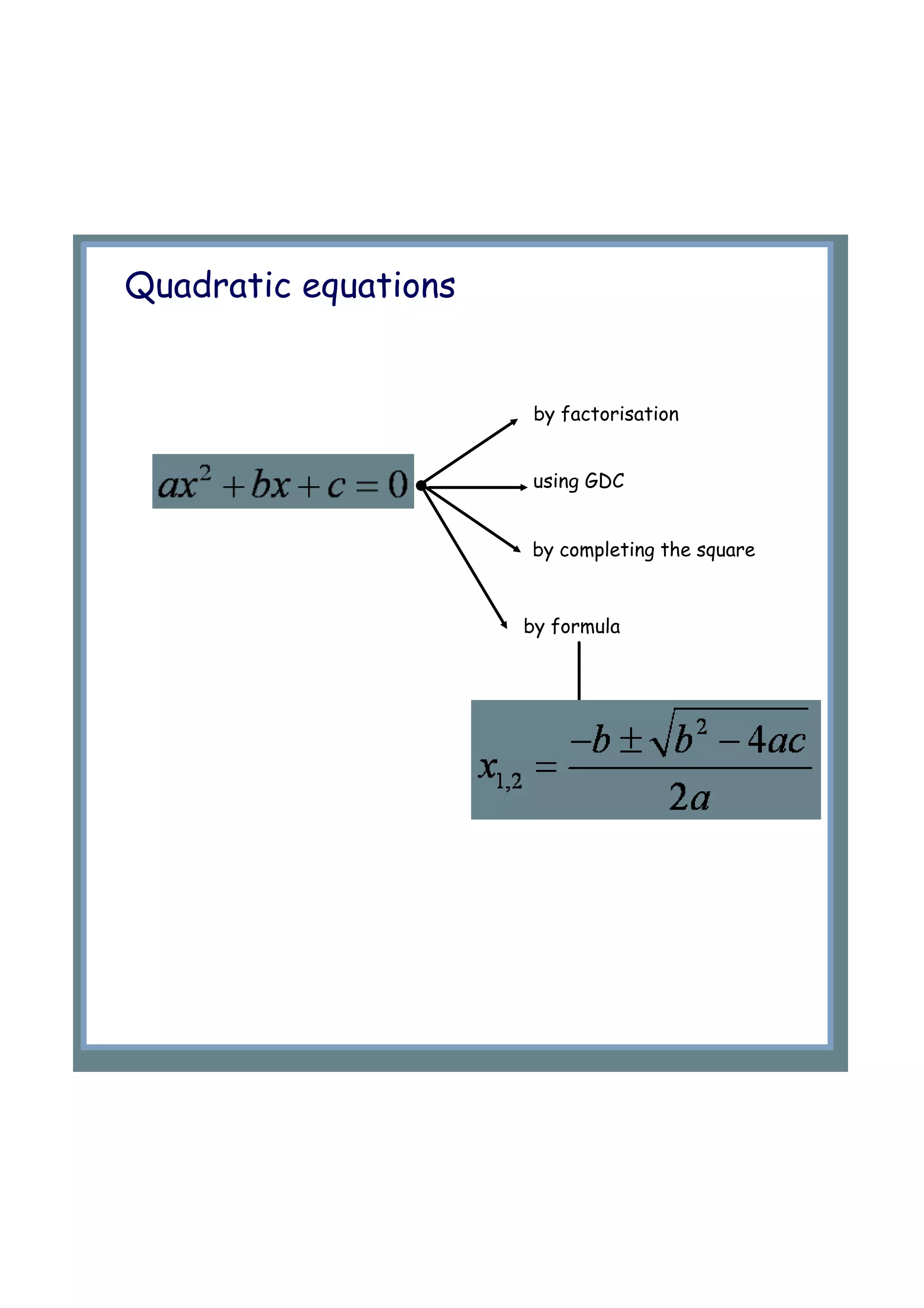












This document discusses solving quadratic equations by different methods such as factorisation, using the quadratic formula, and completing the square. It explains how to determine the number of solutions a quadratic equation has based on the sign of its discriminant, namely: - If the discriminant is positive, there are two real roots - If the discriminant is zero, there is one repeated root - If the discriminant is negative, there are no real roots. Examples are provided to illustrate calculating the discriminant and determining the number and type of roots.













