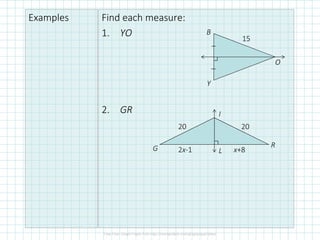
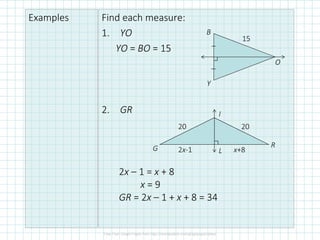
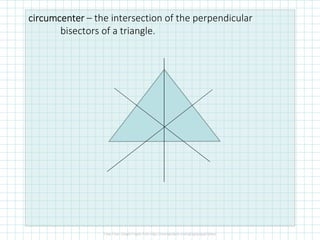
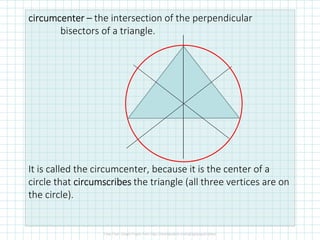
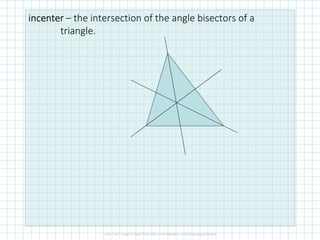
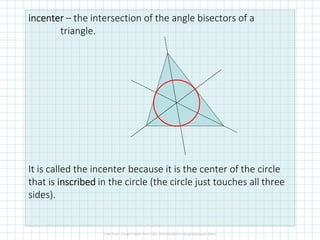
This document discusses perpendicular bisectors, angle bisectors, and how to use them to find the circumcenter and incenter of a triangle. The perpendicular bisector theorem states that if a point is on the perpendicular bisector of a segment, it is equidistant from the endpoints. The angle bisector theorem similarly states that if a point is on the bisector of an angle, it is equidistant from the sides of the angle. The circumcenter is defined as the intersection of the perpendicular bisectors of a triangle, while the incenter is the intersection of the angle bisectors.

1. Perpendicular and Angle Bisectors
The student is able to (I can):
• Construct perpendicular and angle bisectors
• Use bisectors to solve problems
• Identify the circumcenter and incenter of a triangle

2. Perpendicular Bisector Theorem
If a point is on the perpendicular bisector of a segment,
then it is equidistant from the endpoints of the segment.
P
D
A
E
PD = AD
PE = AE

3. Converse of Perpendicular Bisector Theorem
If a point is equidistant from the endpoints of a segment,
then it is on the perpendicular bisector of the segment.
S
K
YT
ST = YT
KT SY⊥

4. Examples Find each measure:
1. YO
2. GR
B
O
Y
15
G
I
R
L
20 20
2x-1 x+8

5. Examples Find each measure:
1. YO
YO = BO = 15
2. GR
B
O
Y
15
G
I
R
L
20 20
2x-1 x+8
2x – 1 = x + 8
x = 9
GR = 2x – 1 + x + 8 = 34

6. Angle Bisector Theorem
If a point is on the bisector of an angle, then it is
equidistant from the sides of the angle.
Converse of the Angle Bisector Theorem
If a point is equidistant from the sides of an angle, then it
is on the angle bisector.
A
L G
N AN = GN
∠ALN ≅ ∠GLN

7. circumcentercircumcentercircumcentercircumcenter – the intersection of the perpendicular
bisectors of a triangle.

8. circumcentercircumcentercircumcentercircumcenter –––– the intersection of the perpendicular
bisectors of a triangle.
It is called the circumcenter, because it is the center of a
circle that circumscribescircumscribescircumscribescircumscribes the triangle (all three vertices are on
the circle).

9. incenterincenterincenterincenter – the intersection of the angle bisectors of a
triangle.

10. incenterincenterincenterincenter – the intersection of the angle bisectors of a
triangle.
It is called the incenter because it is the center of the circle
that is inscribedinscribedinscribedinscribed in the circle (the circle just touches all three
sides).