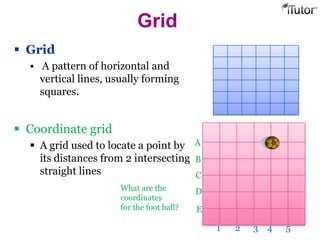
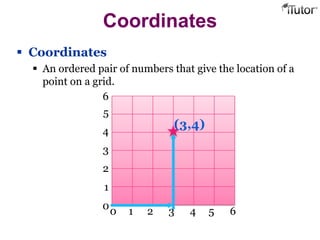
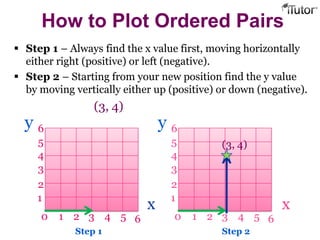
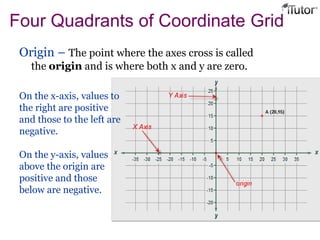
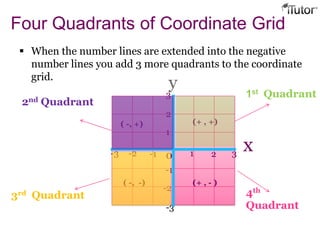
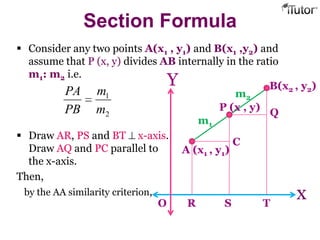
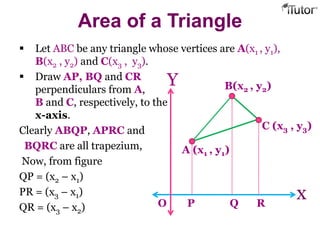
This document provides information about coordinate grids, ordered pairs, and formulas in coordinate geometry. It defines key terms like coordinates, quadrants, and distance and section formulas. The distance formula calculates the distance between two points with coordinates (x1, y1) and (x2, y2). The section formula finds the coordinates of a point that divides a line segment between (x1, y1) and (x2, y2) in a given ratio. It also discusses finding the midpoint and calculating the area of a triangle using coordinates.

1. Coordinate
Grid & Distance Geometry
Formula
T- 1-855-694-8886
Email- info@iTutor.com
By iTutor.com

2. Grid
 Grid
 A pattern of horizontal and
vertical lines, usually forming
squares.
 Coordinate grid
 A grid used to locate a point by
its distances from 2 intersecting
straight lines
A
B
C
D
E
1 2 3 4 5
What are the
coordinates
for the foot ball?

3. The Coordinate Plane
 In coordinate geometry, points are placed on the
"coordinate plane" as shown below.
 It has two scales:
 X axis – A horizontal number line on a coordinate grid.
 Y axis - A vertical number line on a coordinate grid.
1 2 3 4 50 6
x1
2
3
4
5
6
y

4. Coordinates
 Coordinates
 An ordered pair of numbers that give the location of a
point on a grid.
1
2
3
4
5
0
6
1 2 3 4 50 6
(3,4)

5. How to Plot Ordered Pairs
 Step 1 – Always find the x value first, moving horizontally
either right (positive) or left (negative).
 Step 2 – Starting from your new position find the y value
by moving vertically either up (positive) or down (negative).
(3, 4)
1
3
2
4
5
0 1 2 3 4 5 6
y 6
1
3
2
4
5
0 1 2 3 4 5 6
y 6
Step 1 Step 2
x x
(3, 4)

6. Four Quadrants of Coordinate Grid
Origin – The point where the axes cross is called
the origin and is where both x and y are zero.
On the x-axis, values to
the right are positive
and those to the left are
negative.
On the y-axis, values
above the origin are
positive and those
below are negative.

7. Four Quadrants of Coordinate Grid
 When the number lines are extended into the negative
number lines you add 3 more quadrants to the coordinate
grid.
-2 -1
1
2
-3
3
-2
-1
0 1 2
-3
3
y
x
(+ , +)( -, +)
( -, -) (+ , - )
1st Quadrant
2nd Quadrant
3rd Quadrant 4th
Quadrant

8. Four Quadrants
 The following relationship between the signs of the
coordinates of a point and the quadrant of a point in
which it lies.
1) If a point is in the 1st quadrant, then the point will be
in the form (+, +), since the 1st quadrant is enclosed
by the positive x - axis and the positive y- axis.
2) If a point is in the 2nd quadrant, then the point will be
in the form (–, +), since the 2nd quadrant is enclosed
by the negative x - axis and the positive y - axis.

9. Four Quadrants
3) If a point is in the 3rd quadrant, then the point will be
in the form (–, –), since the 3rd quadrant is enclosed
by the negative x - axis and the negative y – axis.
4) If a point is in the 4th quadrant, then the point will be
in the form (+, –), since the 4th quadrant is enclosed
by the positive x - axis and the negative y - axis
x
y
(+, +)(–, +)
(–, –) (+, –)
III
III IV

10. Coordinate Geometry
 A system of geometry where the position of points on
the plane is described using an ordered pair of numbers.
 The method of describing the location
of points in this way was proposed by the
French mathematician René Descartes .
 He proposed further that curves and lines
could be described by equations using this
technique, thus being the first to link
algebra and geometry.
 In honor of his work, the coordinates of a point are often
referred to as its Cartesian coordinates, and the coordinate
plane as the Cartesian Coordinate Plane.
René Déscartes (1596 -1650)

11. Distance Formula
 The distance of a point from the y-axis is called
its x-coordinate, or abscissa.
 The distance of a point from the x-axis is called
its y-coordinate, or ordinate.
 The coordinates of a point on the x-axis are of the
form (x, 0), and of a point on the y-axis are of
the form (0, y).

12. Distance Formula
 Let us now find the distance between any two points
P(x1, y1) and Q(x1, y2)
 Draw PR and QS x-axis.
A perpendicular from the
point P on QS is drawn
to meet it at the point T
So, OR = x1 , OS = x2
, PR = PS = y1
, QS = y2
Then , PT = x2 – x1 ,
QT = y2 – y1
x
Y
P (x1 , y1)
Q(x2 , y2)
T
R SO

13. Distance Formula
 Now, applying the Pythagoras theorem in ΔPTQ, we get
Therefore
222
QTPTPQ
2
12
2
12 yyxx
2
12
2
12 yyxxPQ
which is called the distance formula.

14. Section Formula
 Consider any two points A(x1 , y1) and B(x1 ,y2) and
assume that P (x, y) divides AB internally in the ratio
m1: m2 i.e.
 Draw AR, PS and BT x-axis.
Draw AQ and PC parallel to
the x-axis.
Then,
by the AA similarity criterion, x
Y
A (x1 , y1)
B(x2 , y2)
P (x , y)
R SO T
2
1
m
m
PB
PA
m1
m2
Q
C

15. Section Formula
ΔPAQ ~ ΔBPC
---------------- (1)
Now,
AQ = RS = OS – OR = x– x1
PC = ST = OT – OS = x2– x
PQ = PS – QS = PS – AR = y– y1
BC = BT– CT = BT – PS = y2– y
Substituting these values in (1), we get
BC
PQ
PC
AQ
BP
PA
yy
yy
xx
xx
m
m
2
1
2
1
2
1

16. Section Formula
For x - coordinate
Taking
or
xx
xx
m
m
2
1
2
1
1221 xxmxxm
122121 xmxmxmxmor
or 121221 mmxxmxm
12
1221
mm
xmxm
x

17. Section Formula
For y – coordinate
Taking
yy
yy
m
m
2
1
2
1
1221 yymyym
122121 ymymymym
121221 mmyymym
12
1221
mm
ymym
y
or
or
or

18. Section Formula
So, the coordinates of the point P(x, y) which divides the
line segment joining the points A(x1, y1) and B(x2, y2),
internally, in the ratio m1: m2 are
12
1221
12
1221
,
mm
ymym
mm
xmxm
This is known as the section formula.

19. Mid- Point
• The mid-point of a line segment divides the line segment
in the ratio 1 : 1.
Therefore,
the coordinates of the mid-point P of the join of the
points A(x1, y1) and B(x2, y2) is
From section formula
11
11
,
11
11 1212 yyxx
2
,
2
1212 yyxx

20. Area of a Triangle
 Let ABC be any triangle whose vertices are A(x1 , y1),
B(x2 , y2) and C(x3 , y3).
 Draw AP, BQ and CR
perpendiculars from A,
B and C, respectively, to the
x-axis.
Clearly ABQP, APRC and
BQRC are all trapezium,
Now, from figure
QP = (x2 – x1)
PR = (x3 – x1)
QR = (x3 – x2)
x
Y
A (x1 , y1)
B(x2 , y2)
C (x3 , y3)
P QO R

21. Area of a Triangle
Area of Δ ABC = Area of trapezium ABQP + Area of
trapezium BQRC– Area of trapezium APRC.
We also know that ,
Area of trapezium =
Therefore,
Area of Δ ABC =
embetween thdistancesidesparallelofsum
2
1
PRCR+AP
2
1
CR+BQ
2
1
QPAP+BQ
2
1
QR
133123321212
2
1
2
1
2
1
xxyyxxyyxxyy
133311312333223211211222
2
1
xyxyxyxyxyxyxyxyxyxyxyxy
123312231
2
1
yyxyyxyyx
Area of Δ ABC

22. The End
Call us for more
information
www.iTutor.com
1-855-694-8886
Visit