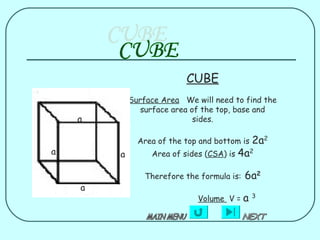
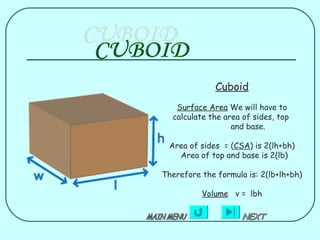
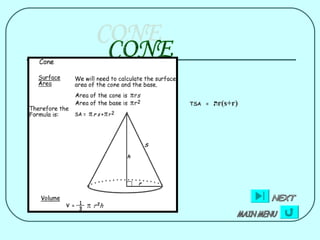
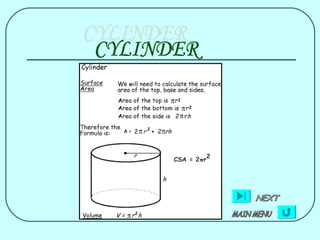
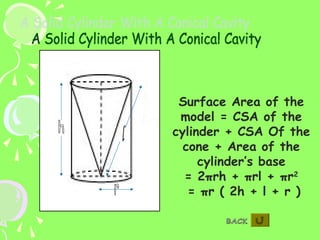
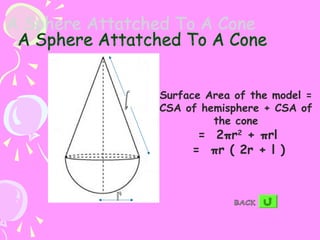
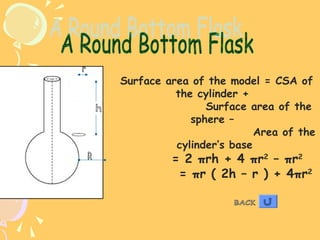
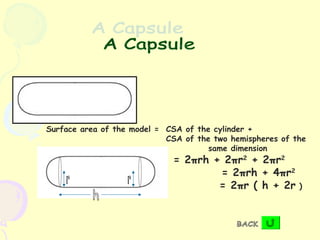
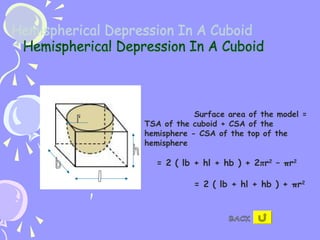
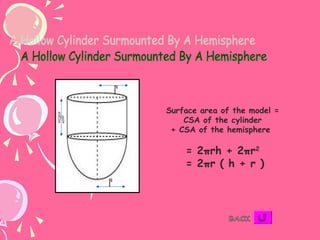
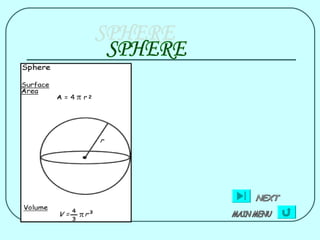
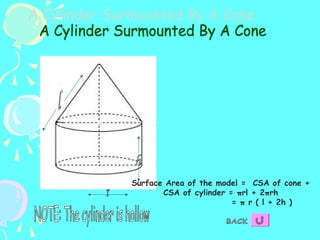
The document provides formulas for calculating the surface area of various 3D geometric shapes like cubes, cuboids, spheres, cylinders, cones, and combinations of shapes. The key information summarized is: 1) Formulas are given for surface area of individual shapes like cubes (6a^2), cuboids (2(lb+lh+bh)), spheres (4πr^2), cylinders (2πrh+2πr^2), and cones (πr(l+2h)). 2) Formulas are also provided for combinations of shapes, for example when two cubes are joined to form a cuboid the surface area is 10a^2. 3) In general,

3. CUBE
Surface Area We will need to find the
surface area of the top, base and
a sides.
Area of the top and bottom is 2a2
a a Area of sides (CSA) is 4a2
Therefore the formula is: 6a2
a
Volume V = a 3

4. Cuboid
Surface Area We will have to
calculate the area of sides, top
and base.
Area of sides = (CSA) is 2(lh+bh)
Area of top and base is 2(lb)
Therefore the formula is: 2(lb+lh+bh)
Volume v = lbh

5. TSA = ‫ת‬r(s+r)

6. 2
CSA = 2πr

8. Surface Area We need to find the
outer surface area and the area of the
base.
Outer surface area (CSA) is 2 π r^2
Area of the base is π r^2
Therefore the formula is 3 π r^2
Volume V = πr^3

11. Surface Area of the model = CSA of cone +
CSA of cylinder = πrl + 2πrh
= π r ( l + 2h )

12. Surface Area of the
model = CSA of the
cylinder + CSA Of the
cone + Area of the
cylinder’s base
= 2πrh + πrl + πr2
= πr ( 2h + l + r )

13. Surface Area of the model =
CSA of hemisphere + CSA of
the cone
= 2πr2 + πrl
= πr ( 2r + l )

14. Surface area of the model = CSA of
the cylinder +
Surface area of the
sphere –
Area of the
cylinder’s base
= 2 πrh + 4 πr2 – πr2
= πr ( 2h – r ) + 4πr2

15. Surface area of the model = TSA of the the larger
cylinder + TSA of the smaller cylinder – Area of the
smaller cylinder’s base
= 2πRH + 2πR2 + 2πrh + 2πr2 – πr2
= 2πR ( H + R ) + 2πr ( h + r )

16. Surface area of the
model = CSA of the
cylinder + CSA of
both the cones
= 2πrh + 2πrl
= 2πr ( h + l )

17. Surface area of the model =
CSA of the cylinder
+ CSA of the
two hemispheres
= 2πrh + 2 ( 2πr2 )
= 2πrh + 4πr2
= 2πr ( h + 2r )

18. When two cubes are joined,
they form a cuboid.
In the given model when the
two cubes of side ‘a’ are joined,
we get a cuboid of dimension >
l = a + a
b = a
h = a
So the model’s surface area is
2 ( lb + bh +hl )
= 2 { ( a + a ) a + a2 + a ( a + a) }
= 2 ( 2a2 + a2 + 2a2 )
= 2 ( 5a2)
= 10a2

19. Surface area of the model = CSA of the cylinder +
CSA of the two hemispheres of the
same dimension
= 2πrh + 2πr2 + 2πr2
= 2πrh + 4πr2
= 2πr ( h + 2r )

20. Surface area of the model =
TSA of the cuboid + CSA of the
hemisphere - CSA of the top of the
hemisphere
= 2 ( lb + hl + hb ) + 2πr2 – πr2
= 2 ( lb + hl + hb ) + πr2

21. Surface area of the model =
TSA of the cuboid + CSA of the
hemisphere - CSA of the top of the
hemisphere
= 2 ( lb + hl + hb ) + 2πr2 – πr2
= 2 ( lb + hl + hb ) + πr2

22. Surface area of the model =
CSA of the cylinder
+ CSA of the hemisphere
= 2πrh + 2πr2
= 2πr ( h + r )

23. • Thank you
- Dhruv Sahdev