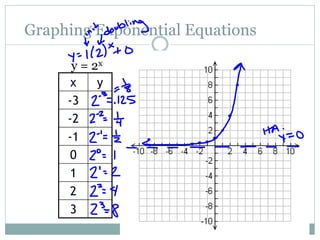
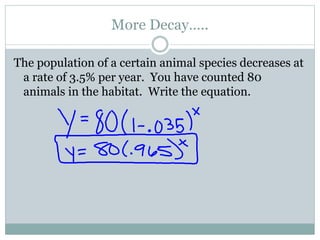
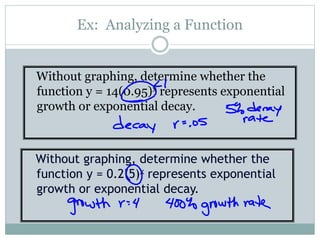
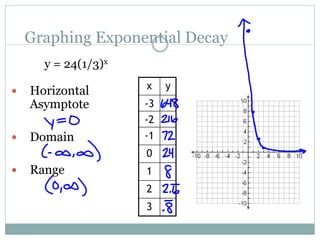
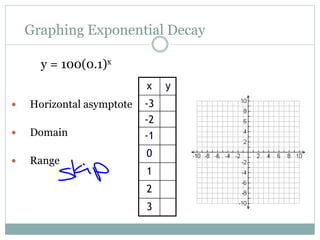
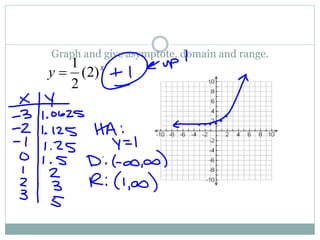
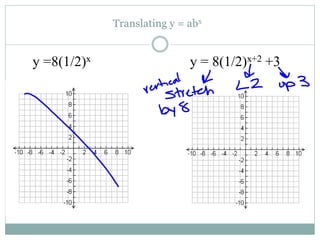
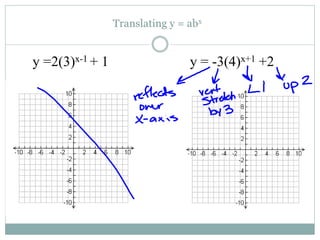
This document provides information about exponential functions and graphs. It defines the general form of an exponential function as y = abx, where a ≠ 0, b > 0, and b ≠ 1. It discusses exponential growth and decay models and provides examples of writing functions to model population growth and depreciation. It also covers graphing exponential functions, including determining horizontal asymptotes, domain and range. It concludes with examples of translating exponential functions by adding or subtracting terms.

1. G R A P H I N G E X P O N E N T I A L S A N D L O G S
Day 2

2. An exponential function is a function with the
general form of:
y = abx
where x is a real number,
a ≠ 0, b > 0, and b ≠ 1.

3. Graphing Exponential Equations
y = 2x
x y
-3
-2
-1
0
1
2
3

4. EXPONENTIAL GROWTH
y = a • bx time
initial amount growth factor (1+r)
Ex. The population of the US in 1994 was about 260
million with an average annual rate of increase
of about 0.7%.
1. Write a function to model this population.
2. What was the population in 2006?

5. Modeling growth
 The bear population increases at a rate
of 2% per year. There are 1573 bears this year.
Write a function that models the bear population.
How many bears will there be in 10 years?

6. Exponential Decay: y = a(1-r)t
Suppose you want to buy a used car that costs
$11,800. The expected depreciation of the car is
20% per year. Estimate the depreciated value of
the car after 6 years.

7. More Decay…..
The population of a certain animal species decreases at
a rate of 3.5% per year. You have counted 80
animals in the habitat. Write the equation.

8. Ex: Analyzing a Function
Without graphing, determine whether the
function y = 14(0.95)x represents exponential
growth or exponential decay.
Without graphing, determine whether the
function y = 0.2(5)x represents exponential
growth or exponential decay.

9. Graphing Exponential Decay
y = 24(1/3)x
 Horizontal
Asymptote
 Domain
 Range
x y
-3
-2
-1
0
1
2
3

10. Graphing Exponential Decay
y = 100(0.1)x
 Horizontal asymptote
 Domain
 Range
x y
-3
-2
-1
0
1
2
3

11. Graph and give asymptote, domain and range.
x
y )2(
2
1


12. Translating y = abx
y =8(1/2)x y = 8(1/2)x+2 +3

13. Translating y = abx
y =2(3)x-1 + 1 y = -3(4)x+1 +2

14. Homework
 Pg. 296 (1-14, 29-34)