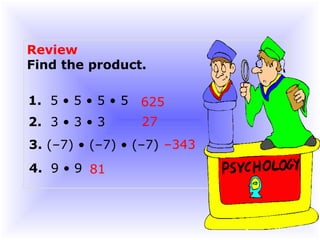
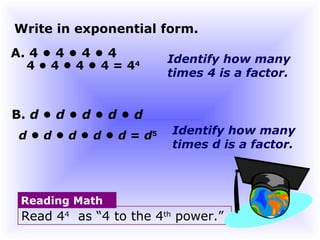
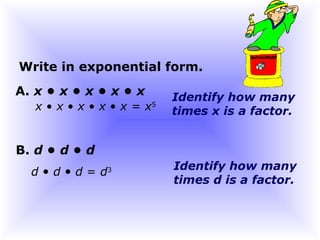
The document is about exponents and power. It begins by introducing exponents, reviewing the rules for evaluating expressions with exponents such as multiplying powers of the same base. It provides examples of simplifying expressions using the laws of exponents such as changing expressions to exponential form, multiplying exponents when multiplying the same base, and evaluating exponential expressions.

1. NAME – ABCD
CLASS -7A
TOPIC -EXPONENTS AND
POWER

3. OBJECTIVE:
The students will simplify
expressions by using the
laws of exponents.

4. Intro to
Exponents
Learn to evaluate
expressions with
exponents.

5. HISTORY of the word
EXPONENT.
• The term EXPONENT
was introduced by
Michael Stifel (1487-
1567) in 1544 in
Arithmetica integra.

6. Review
Find the product.
6251. 5 • 5 • 5 • 5
2. 3 • 3 • 3
3. (–7) • (–7) • (–7)
4. 9 • 9
27
–343
81

7. The term 27
is called a power.
If a number is in exponential
form, the exponent
represents how many times
the base is to be used as a
factor.
7
ExponentBase
2

8. Identify how many
times 4 is a factor.
4 • 4 • 4 • 4 = 44
Write in exponential form.
A. 4 • 4 • 4 • 4
Identify how many
times d is a factor.
d • d • d • d • d = d5
B. d • d • d • d • d
Read 44
as “4 to the 4th
power.”
Reading Math

10. Identify how many
times –6 is a factor.
(–6) • (–6) • (–6) = (–6)3
Identify how many
times 5 is a factor.
5 • 5 = 52
C. (–6) • (–6) • (–6)
D. 5 • 5
Write in exponential form.
Remember to keep the – sign inside the ( )!
If it is outside, your answer will be negative
even if you have an even number of – signs.

11. Exponential Rule:Exponential Rule:
( )
nm mn
x x=
( )
23 3 2 6
Example: 4 4 4×
= =
( ) ( ) ( ) ( )
2 23
6
Proof: 4 4 4 4 4 4 4 4 4 4
4 4 4 4 4 4 4
= × × = × × × × × =
= × × × × × =

12. 15
5•3
53
4
4
)4(
=
=
NOTE:
Multiply the exponents, not add them!
Words Numbers Algebra
To multiply
power of a
power, keep the
base and
multiply the
exponents.
Multiplying Power of a Power
(pr
)s
=
pr
• s
15
5•3
53
4
4
)4(
=
=

13. Identify how many
times x is a factor.x • x • x • x • x = x5
Write in exponential form.
A. x • x • x • x • x
Identify how many
times d is a factor.
d • d • d = d3
B. d • d • d

16. A. 35
= 243
35
= 3 • 3 • 3 • 3 • 3
Find the product of
five 3’s.
= –243
= (–3) • (–3) • (–3) • (–3) • (–3)(–3)5
Find the product of five –3’s.B. (–3)5
Always use parentheses to raise a negative
number to a power.
Helpful Hint
Evaluate.

17. C. 74
= 2401
74
= 7 • 7 • 7 • 7
Find the product of four 7’s.
= –729
= (–9) • (–9) • (–9)(–9)3
Find the product of three –9’s.D. (–9)3
Evaluate.

18. Simplifying Expressions
= 47
Simplify (25
– 32
) + 6(4)
= (32 – 9) + 6(4)
= (23) + 6(4)
= 23 + 24
Evaluate the exponents.
Subtract inside the parentheses.
Multiply from left to right.
Add from left to right.

19. = –49
Simplify (32
– 82
) + 2 • 3
= (9 – 64) + 2 • 3
= (–55) + 2 • 3
= –55 + 6
Evaluate the exponents.
Subtract inside the parentheses.
Multiply from left to right.
Add from left to right.