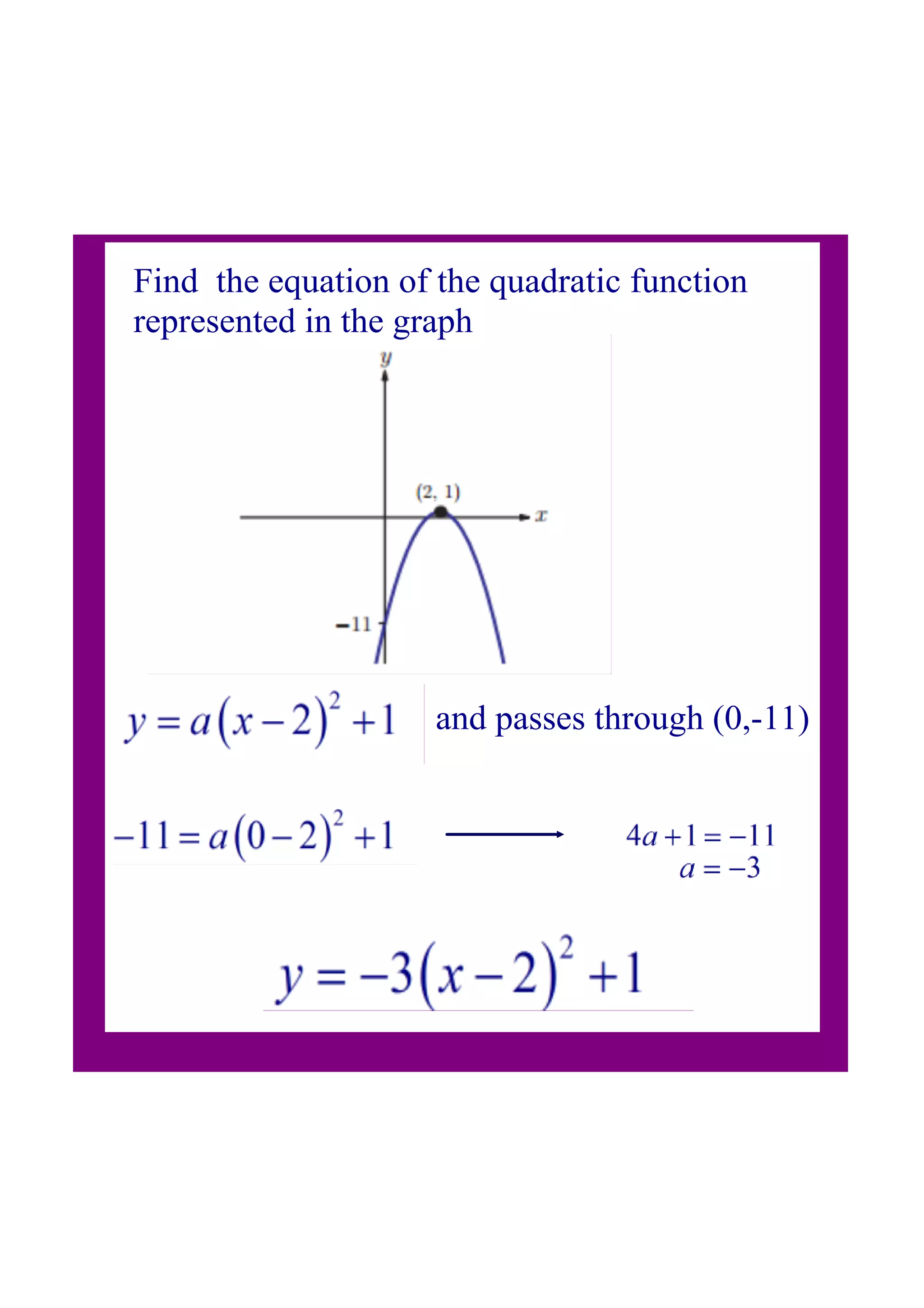
The document discusses quadratic functions and their graphs. It aims to explore the properties of quadratic functions and express them in different forms, including vertex form. It provides examples of writing quadratic functions in vertex form given the vertex, as well as writing the function in general form given its vertex. The key points are that the vertex form of a quadratic function y = a(x - h)2 + k shows the vertex is (h, k) and the line of symmetry is x = h. Converting between the vertex and general forms allows finding the maximum point of a quadratic function.

1. To explore the properties of quadratic functions
and their graphs.
To investigate the different forms in which
quadratic functions can be expressed.
To express a quadratic function in vertex form.
http://www.youtube.com/watch?v=VSUKNxVXE4E&feature=player_embedded#
http://evmaths.jimdo.com/year­11/functions/?logout=1

2. Draw sketches of these quadratic functions
with the help of your calculator and state
the vertex in each case,
V=
V=
V=
V=

3. is called Vertex Form or completed square form
A quadratic function y = a (x ­ h )2
+ k has its
vertex in (h , k) and line of symmetry x = h.

4. Let's go back to the examples:
V= (5 , 3)
write this quadratic in general form, thus find
a, b and c
line of symmetry: x = 5
a =2 b = ­ 20 c = 53
line of symmetry:

5. Let's go back to the examples:
V= (­5 , 3)
write this quadratic in general form, thus find
a, b and c
line of symmetry: x = ­5
a =1 b = 10 c = 28
line of symmetry:

6. Let's go back to the examples:
V= (2 , 7)
write this quadratic in general form, thus find
a, b and c
line of symmetry: x = 2
a = ­3 b = 12 c = ­ 5
line of symmetry:

7. a)Write the function y = ­ x2
+ 4 x ­ 3 in the
form y =a( x ­ h )2
+k , hence state its maximum
point.
b) Solve the equation y = ­ 8
a= ­1, b= 4 , c =­ 3
line of symmetry: x =2
vertex or maximum point will be when x = 2
when x = 2 then y = ­(2)2
+4(2)­3= 1
so V = ( 2, 1)

8. b) Solve the equation y = ­ 8

9. Find the equation of the quadratic function
represented in the graph
and passes through (0,­11)

10. Solve Ex 1 B page 11