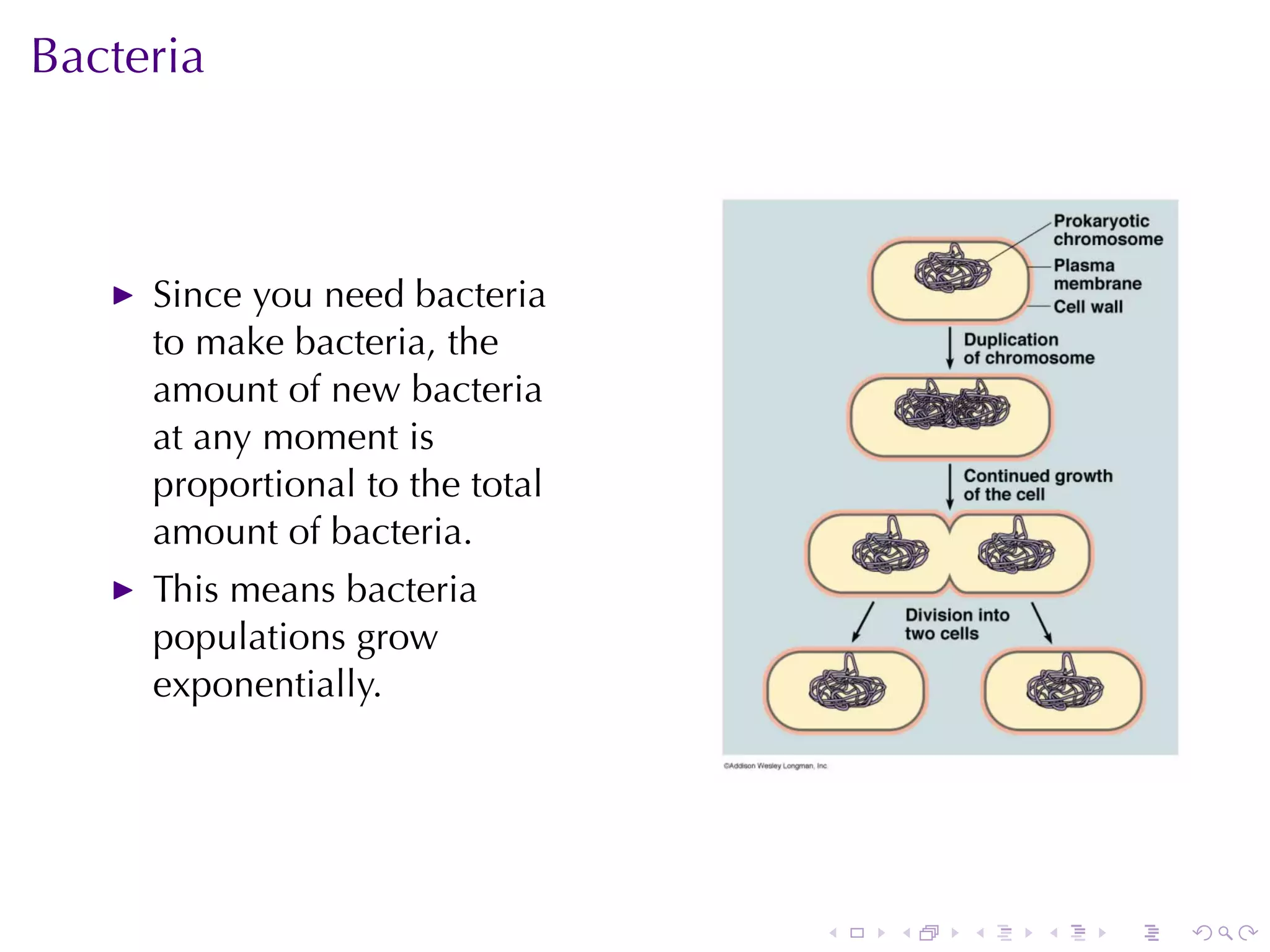
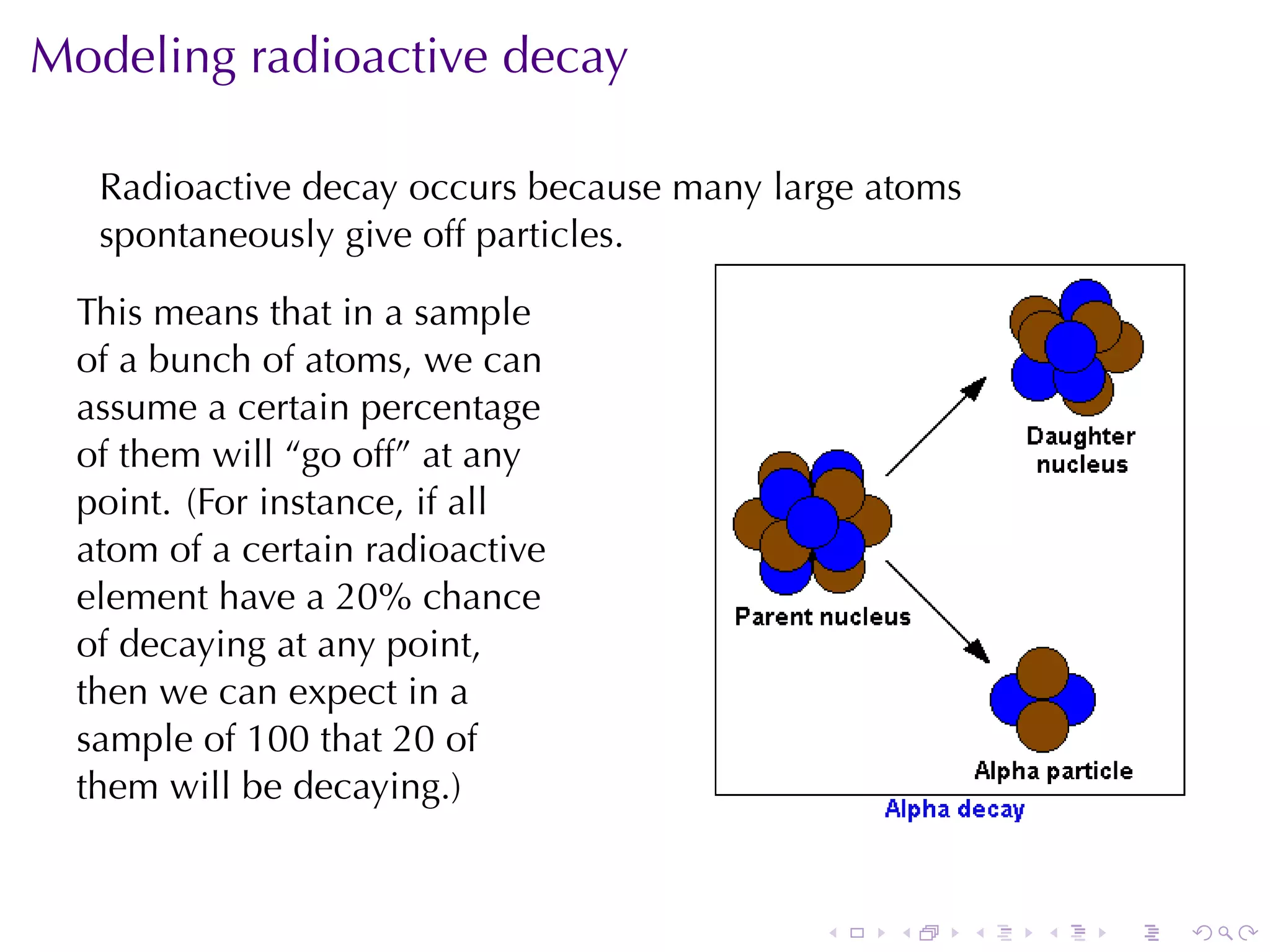
The document discusses various mathematical models involving exponential growth and decay, including population growth, radioactive decay, and continuously compounded interest. It defines differential equations and provides examples of how to solve them, particularly focusing on real-world applications such as carbon-14 dating and Newton's law of cooling. Several examples illustrate the principles of exponential functions in different contexts, highlighting their significance in calculus.