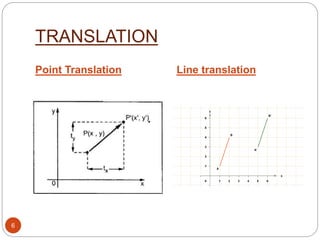
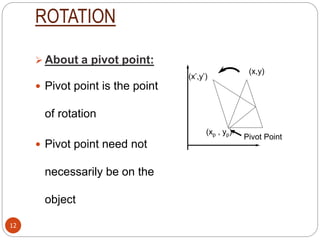
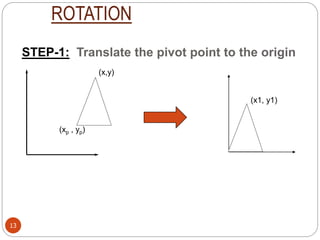
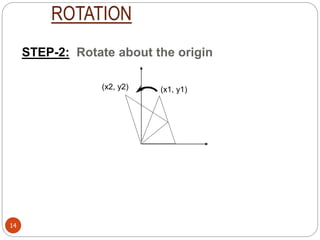
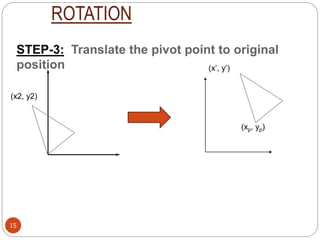
This document discusses 2D transformations including translation and rotation. Translation moves an object to a new position by adding a translation vector to the original coordinates. Rotation changes the orientation of an object by a certain angle. Rotation can occur around the origin or a pivot point, with the latter requiring three steps - translate to origin, rotate, translate back. The document provides examples and matrix representations of these transformations.

1. 2D-TRANSLATION
&
ROTATION
(W.R.T ORIGIN &PIVOT POINT)
1

2. TRANSFORMATION
 Transformation means changing some graphics into
something else by applying rules.
 Types
 Translation,
 Scaling
 Rotation,
 Shearing
 Reflection
2

3. TRANSLATION
 Translation moves an object to a different position
on the screen.
 It can be described as a rigid motion.
 It changes the position of object.
3

4. TRANSLATION
 A point can be translated in 2D by adding translation
coordinate (tx, ty) to the original coordinate (X, Y) to
get the new coordinate (X’, Y’).
 i.e. X’=X+ tx
Y’=Y+ ty
 (tx, ty) is called the translation vector or shift vector.
4

5. TRANSLATION
 Matrix
Representation:
 1 0 0
0 1 0
tx ty 1
• (tx ,ty)= translation factor.
5

6. TRANSLATION
Point Translation Line translation
6

7. QUESTION
7
Q. Consider a unit square and translate it to 3-units in
x-direction and 3-units in y-direction.
given:
tx=3-units
ty=3-units
Co-ordinates of the unit square: A(0,0);
B(1,0);C(1,1);D(0,1).

8. ROTATION
8
 Change in orientation.
 Rigid body transformation.
 Types:
 about origin(0,0)
 about a pivot point

9. ROTATION
9
 About origin:
 In rotation, we rotate the object at particular angle θ
(theta) from its origin.
 It can be described as rigid body transformation.
 It is change in orientation.
 Convention:
Θ positive: rotation counter clockwise.
Θ negative: rotation clockwise.

10. ROTATION
 The point P(X, Y) is
located at angle φ
from the horizontal X
coordinate with
distance r from the
origin.
 We rotate it at the
angle θ. After rotating
it to a new location,
we get a new point P’
(X’, Y’).
10

11. ROTATION
11
 Matrix
Representation:
cos θ -sin θ
0
sin θ cos θ
0
0 0
1
 Question:
Rotate a triangle
A(0,0);
B(1,1), C(5,2) about
origin by 45degrees.
Given: angle of
rotation=45
degrees.

12. ROTATION
12
 About a pivot point:
 Pivot point is the point
of rotation
 Pivot point need not
necessarily be on the
object
(xp , yp)
(x,y)
(x’,y’)
Pivot Point

13. 13
(xp , yp)
(x,y)
(x1, y1)
STEP-1: Translate the pivot point to the origin
ROTATION

14. 14
(x1, y1)
STEP-2: Rotate about the origin
(x2, y2)
ROTATION

15. 15
STEP-3: Translate the pivot point to original
position
(x2, y2)
(xp, yp)
(x’, y’)
ROTATION

16. ROTATION
16
 About pivot point matrix representation:
1 0 0 1 0 cos θ 1 0 0
0 1 0 0 1 - sin θ 0 1 0
-tx -ty 1 0 0 1 tx ty 1
• (tx,ty)=translation factor
• Θ=angle of rotation.

17. Question
17
Q. Rotate a triangle with co-ordinates A(0,0);
B(1,1);C(5,2) about a pivot point (1,1) by
45degrees.
Given:
pivot point=(0,0)
angle of rotation=45 degrees.
Step1: translate the triangle to origin.(tx=-1,ty=-1)
Step 2: rotate the triangle by 45degrees.
Step 3: translate the triangle back to the pivot point.
(tx=1, ty=1)

18. 18
THANK YOU