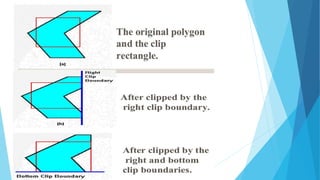
This document discusses two computer graphics algorithms: the Sutherland-Hodgman polygon clipping algorithm and the scan line fill algorithm. The Sutherland-Hodgman algorithm clips polygons against the boundaries of a clip window by testing each polygon edge against each clip window edge. The scan line fill algorithm fills polygons by drawing between intersection points of polygon edges and horizontal scan lines from top to bottom. It handles polygon corners and edge endpoints to correctly determine the interior and exterior regions.

1. POLYGON CLIPPING WITH
SUTHERLAND HODGEMAN
ALGORITHM
AND
SCAN LINE FILL ALGORITHM

2. Clipping
 The primary use of clipping in computer graphics is to remove
objects, lines, or line segments that are outside the viewing pane .
Clip Window: The region against which an object is to be clipped.
 Point Clipping
 Line Clipping (straight-line segments)
 Area Clipping (polygons)
 Text Clipping

3. Polygon Clipping
 Clipping a polygon fill area needs more than line-clipping of the
polygon edges
-would produce and unconnected set of lines
 Must generate one or more closed polylines, which can be filled with
the assigned colour or pattern

4. Sutherland–Hodgeman algorithm
 Each edge of the polygon must be tested against each edge of the clip
rectangle; new edges must be added, and existing edges must be
discarded, retained, or divided. Multiple polygons may result from
clipping a single polygon. We need an organized way to deal with all
these cases

5. FOUR POSSIBLE SCENARIOS AT EACH CLIPPER
Each edge goes through 4 clippers .The rule for each edge for each clipper is:
 If first input vertex is outside, and second is inside, output the intersection and
the second vertex
 If first both input vertices are inside, then just output second vertex
 If first input vertex is inside, and second is outside, output is the intersection
 If both vertices are outside, output is nothing

6. Steps of Sutherland-Hodgmans polygon
clipping algorithm
 Polygons can be clipped against each edge of the window one at a
time.
 Vertices which are kept after clipping against one window edge are
saved for clipping against the remaining edges .
 Note that the number of vertices usually changes and will often
increases.

9. SCAN LINE FILL ALGORITHM

10. Scan-Line
 A scan line is one line, or row, in a raster scanning
pattern, such as a line of video on a cathode ray
tube display of a television set or computer
monitor.

11. Scan-line Polygon Fill
For each scan-line :
 Locate the intersection of the scan-line with the edges (y=ys)
 Sort the intersection points from left to right.
 Draw the interiors intersection points pairwise. (a-b), (c-d)

12. Problem with corners. Same point counted twice or not?
 a,b,c and d are intersected by 2 line segments each.
 Count b,c twice but a and d once. Why?
Solution:
Make a clockwise or counter-clockwise traversal on edges.
Check if y is monotonically increasing or decreasing. If
direction changes, double intersection, otherwise single
intersection.

13. Scan Line Fill: What happens at edge
end-point?
 Edge endpoint is duplicated.
 In other words, when a scan line intersects an edge endpoint, it
intersects two edges.
 Two cases:
Case A: edges are monotonically increasing or decreasing
Case B: edges reverse direction at endpoint
 In Case A, we should consider this as only ONE edge
intersection
 In Case B, we should consider this as TWO edge intersections

14. Scan Line Fill Algorithm
Basic algorithm:
 Assume scan line start from the left and is outside the polygon.
 When intersect an edge of polygon, start to color each pixel (because
now we’re inside the polygon), when intersect another edge, stop
coloring …
 Odd number of edges: inside
 Even number of edges: outside

15. THANK YOU