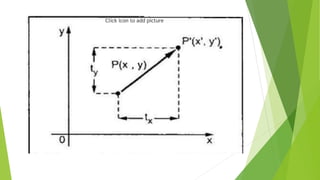
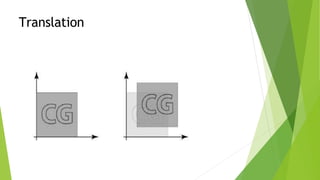
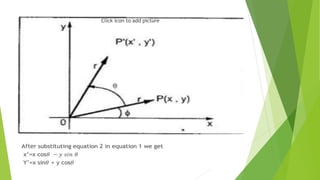
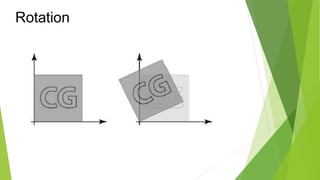
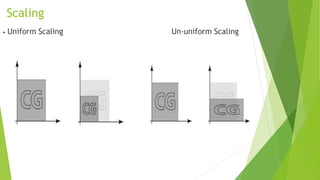
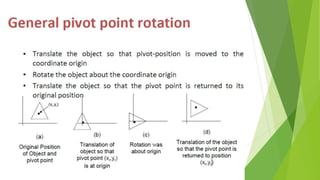
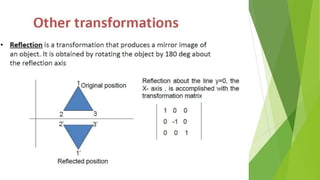
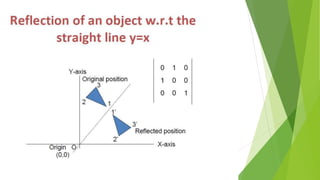
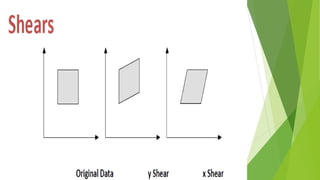
This document discusses 2D transformations in computer graphics, including translation, rotation, and scaling. Translation moves an object by adding offsets to x and y coordinates. Rotation uses trigonometry and rotation matrices to reposition objects around a central point. Scaling enlarges or shrinks objects by multiplying their coordinates by scaling factors. Homogeneous coordinates allow representing these transformations with matrix multiplications.

1. 2D TRANSFORMATIONS
COMPUTER GRAPHICS

2. 2D Transformations
“Transformations are the operations applied to
geometrical description of an object to change its
position, orientation, or size are called geometric
transformations”.

3. Translation
❖ Translation is a process of changing the position
of an object in a straight-line path from one co-
ordinate location to another.
❖ We can translate a two dimensional point by
adding translation distances, tx and ty.
❖ Suppose the original position is (x ,y) then new
position is (x’, y’).
❖ Here x’=x + tx and y’=y + ty.

4. Click icon to add picture

5. Translation

6. ❖ Matrix form of the equations:
X’ = X + tx and Y’ = Y + ty is
P = x
y
P’ = x’
y’
T= tx
ty
❖ we can write it,
P’= P + T

7. ❖ Translate a polygon with co-ordinates A(2,5) B(7,10) and C(10,2) by 3
units in X direction and 4 units in Y direction.
❖ A’ = A +T
= 2 +
5
3 =
4
5
9
❖ B’ = B + T
= 7
10
C’ = C + T
+ 3 =
4
10
14
❖
= 10 + 3 =
2 4
13
7

8. Rotation
❖ A two dimensional rotation is applied to an object by
repositioning it along a circular path in the xy plane.
❖ Using standard trigonometric equations , we can express
the transformed co-ordinates in terms of
x’ = r cos( coscosr sinsin
y’ = r sin( cosr sin
❖ The original co-ordinates of the point is
x = r cos
y = r sin

9. Click icon to add picture
After substituting equation 2 in equation 1 we get
x’=x cos
Y’=x sin + y cos

10. Rotation

11. ❖ That equation can be represented in matrix form
x’ y’ = x y cos
-sin cos
❖ we can write this equation as,
P’ = P . R
❖ Where R is a rotation matrix and it is given as
R = cos
-sin cos

12. ❖ A point (4,3) is rotated counterclockwise by angle of 45.
find the rotation matrix and the resultant point.
❖ R = cos =
- cos
cos45
-sin45
= 1/√2
sin45
cos45
1/√2
- 1/√2 1/√2
P’ = 4 3 1/√2 1/√2
- 1/√2 1/√2
= 4/√2 – 3/√2 4/√2 + 3/√2
= 1/√2 7/√2

13. Scaling
❖ A scaling transformation changes the size of an object.
❖ This operation can be carried out for polygons by
multiplying the co-ordinates values (x , y) of each vertex
by scaling factors Sx and Sy to produce the transformed
co-ordinates (x’ , y’).
x’ = x . Sx
y’ = y . Sy
❖ In the matrix form
x’ y’ = x y Sx 0
0 Sy
= P . S

14. Scaling
• Uniform Scaling Un-uniform Scaling

15. Homogeneous co-ordinates for Translation
❖ The homogeneous co-ordinates for translation are given as
T = 1 0 0
0 1 0
tx ty 1
❖ Therefore , we have
x’ y’ 1 = x y 1 1 0 0
0 1 0
tx ty 1
= x + tx y + ty 1

16. Homogeneous co-ordinates for rotation
❖ The homogeneous co-ordinates for rotation are given as
R = cos sin
-sin cos
0 0 1
❖ Therefore , we have
x’ y’ 1 = x y 1 cos sin
-sin cos
0 0 1
= x cos - y sin x sin + y cos 1

17. Homogeneous co-ordinates for scaling
❖ The homogeneous co-ordinate for scaling are given as
S = Sx 0 0
0 Sy 0
0 0 1
= x . Sx y . Sy
❖ Therefore , we have
x’ y’ 1 = x y 1 Sx 0 0
0 Sy 0
0 0 1
1

28. CONCLUSION
T o manipulate the initially created
object and to display the
modified object without having to
redraw it, we use
Transformations.

29. THANK YOU