The document discusses control strategies for wind turbines. It begins by outlining the four major steps in developing a wind turbine control system: 1) define clear control objectives, 2) select suitable control strategies, 3) decide how to realize the control strategy, and 4) design the controller. The objectives of wind turbine controls are then defined as maximizing energy capture while preventing excessive mechanical loads and ensuring power quality. The document goes on to explain how the aerodynamic torque on the turbine changes based on wind speed and rotor speed.

1. Wind Energy I
Control strategies
Michael Hölling, WS 2010/2011 slide 1

2. Wind Energy I Class content
5 Wind turbines in
general 6/7 Wind - blades
2 Wind measurements interaction
8 Power losses at
the rotor blade
9 Control strategies
3 Wind field
characterization
4 Wind power 10 Generator
11 Electrics / grid
Michael Hölling, WS 2010/2011 slide 2

3. Wind Energy I Control objectives and strategies
Development of a wind turbine control system can be divided
into four major steps:
define clearly control objectives
selection of suitable control strategies which determines the operation point
of the wind turbine for each wind speed
decide how the control strategy will be realized --> selection of the control
schemes, the controlled variables, the reference signals, the switching
procedure between different controllers, etc.
design of the input-output map, meaning the characteristics of the
controller according to the specifications
Michael Hölling, WS 2010/2011 slide 3

4. Wind Energy I Control objectives
Control objectives for wind turbines
Energy capture: Maximization of energy capture taking into
account safe operation restrictions such as rated power, rated
speed and cut-out wind speed, etc.
Mechanical loads: Preventing WECS from excessive dynamic
mechanical loads. This general goal includes reduction of transient
loads, reduction of high frequency loads and resonance avoidance.
Power quality: Conditioning the generated power to comply with
interconnection standards.
Michael Hölling, WS 2010/2011 slide 4

5. Wind Energy I Operation point
Where / what is the steady-state of operation ?
the steady-state of operation is reached when the aerodynamic torque
developed by the rotor equals the reaction torque of the generator
net torque applied to the system is zero
At the steady-state operation point the aerodynamical power
equals the converted power (minus losses at the generator):
Pae = Pgen
Tae · ω = Tgen · ω
ω · (Tae − Tgen ) = 0 ⇒ Tae − Tgen = 0
Michael Hölling, WS 2010/2011 slide 5

6. Wind Energy I Torque and power coefficient
How does the aerodynamic torque change with u1 ?
Aerodynamic torque Tae:
Tae = Fae · R · cT
1
Tae = · ρ · π · R2 · u2 · R · cT
2 1
The power converted by the WEC is given by:
PW EC = Tae · ω = Pair · cp
1
⇒ cT = cp ·
λ
Michael Hölling, WS 2010/2011 slide 6

7. Wind Energy I Aerodynamic torque
The torque coefficient can be determined from the power
coefficient. Until now we determined the maximum power
coefficient by taking into consideration:
Betz limit with the expansion by Schmitz
losses at the rotor blades (drag losses and tip losses)
0.6 cpSchmitz
cpSchmitz, z=3,"(#)=60
0.4
These curve represents the
cpr(!)
maximum power coefficient
0.2
for each tip speed ratio BUT
λ0
design is only possible for one
0.0
0 5 10 15 20 tip speed ratio λ0!
!
Michael Hölling, WS 2010/2011 slide 7

8. Wind Energy I Aerodynamic torque
Without control system the WEC is designed and optimized
for one u1 and one ω.
0.6
cpr(!) 0.4
0.2
λ0
0.0
0 5 10 15 20
!
u2= 2/3.u1 u2= 2/3.u*1
the angle of
urot urot attack changes
β ures by changing u1 β* u*res and cl(α) to cl(α*)
to u*1 and with and cd(α) to cd(α*)
α it λ το λ* as well
α*
Michael Hölling, WS 2010/2011 slide 8

9. Wind Energy I Aerodynamic torque
0.6 cp From Betz we know that there is one
optimum ratio between u3 and u1.
0.4
The WEC meets this at the design for
cp
0.2 λ0.
λ0
0.0
0.0 0.5 1.0
u3/u1
The cp coming from Betz in cpSchmitz
0.6
combination with the cpSchmitz,
changing angle of attack 0.4 z=3,"(#)=60
for different u1, we get a cp! (!,#)
cpr(!)
0
power coefficient that 0.2
depends on λ and α - λ0
cp(λ,α) 0.0
0 5 10 15 20
!
Michael Hölling, WS 2010/2011 slide 9

10. Wind Energy I Aerodynamic torque
Note: In reality λmax and λ0 must NOT necessarily coincide !!
1
With cT = cp · cp(λ) and cT(λ) can be plotted:
⇒
λ
0.6 0.15
cp(!)
cT(!)
0.4 0.10
cT(!)
cp(!)
0.2 0.05
0.0 0.00
0 4 8 12
!
Michael Hölling, WS 2010/2011 slide 10

11. Wind Energy I Aerodynamic torque
How does the torque change with changing ω for different but
fixed u1? 1 ω·R 1
Tae = · ρ · π · R2 · u3 · cp ·
2 1
u1 ω
λ
0.6
cp(!)
0.4
cp(!)
cp(!)
0.2
0.0
0 4 8 12
! !
Michael Hölling, WS 2010/2011 slide 11

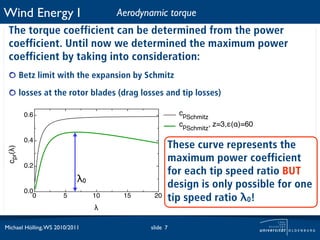
12. Wind Energy I Aerodynamic torque
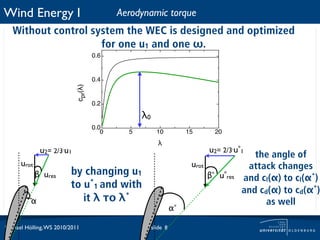
How does the torque change with changing ω for different but
fixed u1? 1 ω·R 1
Tae = · ρ · π · R2 · u3 · cp ·
2 1
u1 ω
λ
u1 = 25m/s
torque [Nm]
cp(!)
! !
Michael Hölling, WS 2010/2011 slide 12

13. Wind Energy I Aerodynamic torque
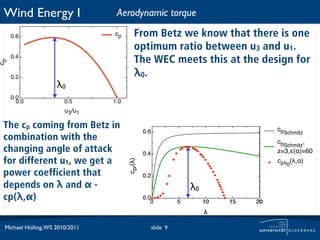
How does the torque change with changing ω for different but
fixed u1? 1 ω·R 1
Tae = · ρ · π · R2 · u3 · cp ·
2 1
u1 ω
λ
u1 = 25m/s
u1 = 22m/s
torque [Nm]
cp(!)
! !
Michael Hölling, WS 2010/2011 slide 13

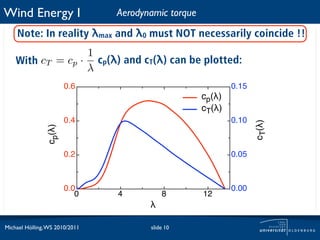
14. Wind Energy I Aerodynamic torque
How does the torque change with changing ω for different but
fixed u1? 1 ω·R 1
Tae = · ρ · π · R2 · u3 · cp ·
2 1
u1 ω
λ
u1 = 25m/s
u1 = 22m/s
torque [Nm]
u1 = 20m/s
cp(!)
! !
Michael Hölling, WS 2010/2011 slide 14

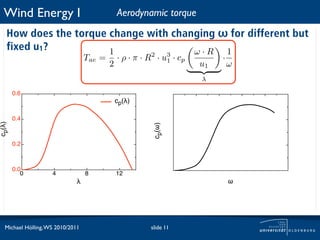
15. Wind Energy I Aerodynamic torque
How does the torque change with changing ω for different but
fixed u1? 1 ω·R 1
Tae = · ρ · π · R2 · u3 · cp ·
2 1
u1 ω
λ
u1 = 25m/s
u1 = 22m/s
torque [Nm]
u1 = 20m/s
u1 = 17m/s
cp(!)
! !
Michael Hölling, WS 2010/2011 slide 15

16. Wind Energy I Aerodynamic torque
How does the torque change with changing ω for different but
fixed u1? 1 ω·R 1
Tae = · ρ · π · R2 · u3 · cp ·
2 1
u1 ω
λ
u1 = 25m/s
u1 = 22m/s
torque [Nm]
u1 = 20m/s
u1 = 17m/s
cp(!)
u1 = 14m/s
! !
Michael Hölling, WS 2010/2011 slide 16

17. Wind Energy I Aerodynamic torque
How does the torque change with changing ω for different but
fixed u1? 1 ω·R 1
Tae = · ρ · π · R2 · u3 · cp ·
2 1
u1 ω
λ
u1 = 25m/s
u1 = 22m/s
torque [Nm]
u1 = 20m/s
u1 = 17m/s
cp(!)
u1 = 14m/s
u1 = 12m/s
! !
Michael Hölling, WS 2010/2011 slide 17

18. Wind Energy I Aerodynamic torque
How does the torque change with changing ω for different but
fixed u1? 1 ω·R 1
Tae = · ρ · π · R2 · u3 · cp ·
2 1
u1 ω
λ
u1 = 25m/s
u1 = 22m/s
torque [Nm]
u1 = 20m/s
u1 = 17m/s
cp(!)
u1 = 14m/s
u1 = 12m/s
u1 = 10m/s
! !
Michael Hölling, WS 2010/2011 slide 18

19. Wind Energy I Aerodynamic torque
How does the torque change with changing ω for different but
fixed u1? 1 ω·R 1
Tae = · ρ · π · R2 · u3 · cp ·
2 1
u1 ω
λ
u1 = 25m/s
u1 = 22m/s
torque [Nm]
u1 = 20m/s
u1 = 17m/s
cp(!)
u1 = 14m/s
u1 = 12m/s
u1 = 10m/s
u1 = 8m/s
! !
Michael Hölling, WS 2010/2011 slide 19

20. Wind Energy I Aerodynamic torque
How does the torque change with changing ω for different but
fixed u1? 1 ω·R 1
Tae = · ρ · π · R2 · u3 · cp ·
2 1
u1 ω
λ
u1 = 25m/s
u1 = 22m/s
torque [Nm]
u1 = 20m/s
u1 = 17m/s
cp(!)
u1 = 14m/s
u1 = 12m/s
u1 = 10m/s
u1 = 8m/s
u1 = 6m/s
! !
Michael Hölling, WS 2010/2011 slide 20

21. Wind Energy I Aerodynamic torque
How does the torque change with changing ω for different but
fixed u1? 1 ω·R 1
Tae = · ρ · π · R2 · u3 · cp ·
2 1
u1 ω
λ
u1 = 25m/s
u1 = 22m/s
torque [Nm]
u1 = 20m/s
u1 = 17m/s
cp(!)
u1 = 14m/s
u1 = 12m/s
u1 = 10m/s
u1 = 8m/s
u1 = 6m/s
u1 = 4m/s
! !
Michael Hölling, WS 2010/2011 slide 21

22. Wind Energy I Aerodynamic torque
How does the torque change with changing ω for different but
fixed u1? 1 ω·R 1
Tae = · ρ · π · R2 · u3 · cp ·
2 1
u1 ω
λ
u1 = 25m/s
u1 = 22m/s
torque [Nm]
u1 = 20m/s
u1 = 17m/s
cp(!)
u1 = 14m/s
u1 = 12m/s
u1 = 10m/s
u1 = 8m/s
u1 = 6m/s
u1 = 4m/s
! !
Tcpmax
Michael Hölling, WS 2010/2011 slide 22

23. Wind Energy I Aerodynamic torque
How does the torque change with changing ω for different but
fixed u1? 1 ω·R 1
Tae = · ρ · π · R2 · u3 · cp ·
2 1
u1 ω
λ
u1 = 25m/s
u1 = 22m/s
torque [Nm]
u1 = 20m/s
u1 = 17m/s
cp(!)
u1 = 14m/s
u1 = 12m/s
u1 = 10m/s
u1 = 8m/s
u1 = 6m/s
u1 = 4m/s
! !
Tcpmax
Trated power
Michael Hölling, WS 2010/2011 slide 23

24. Wind Energy I Control strategies
Points in this torque-rotational speed plane (Tae-ω plane) that
intersect with the generator torque define the steady-state
operating conditions of the WEC. Different WEC control
strategies results in different power curves P(u1), power
coefficients cp(u1) and dynamical behavior.
Different strategies are:
fixed-speed, fixed-pitch (FS-FP)
variable-speed, fixed-pitch (VS-FP)
fixed-speed, variable-pitch (FS-VP)
variable speed, variable-pitch (VS-VP)
Michael Hölling, WS 2010/2011 slide 24

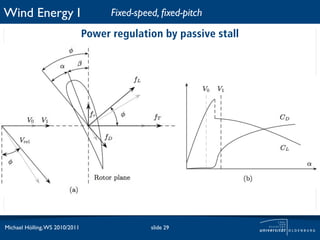
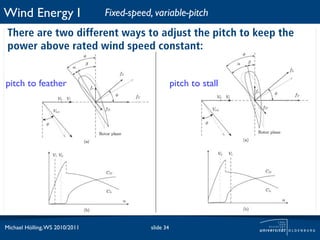
25. Wind Energy I Control strategies
The interesting region for the control system is marked in the
red box.
u1 = 25m/s
u1 = 22m/s
torque [Nm]
u1 = 20m/s
u1 = 17m/s
u1 = 14m/s
u1 = 12m/s
u1 = 10m/s
u1 = 8m/s
u1 = 6m/s
u1 = 4m/s
!
Tcpmax
Trated power
Michael Hölling, WS 2010/2011 slide 25

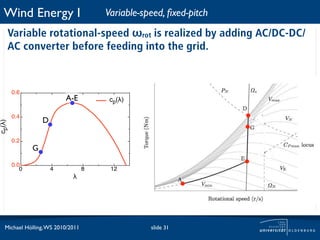
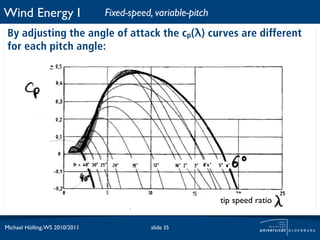
26. Wind Energy I Fixed-speed, fixed-pitch
Fixed rotational-speed ω0 is realized by coupling an
asynchronous generator directly to the grid.
0.6
B u1 = 17m/s
cp(!) u1max u1 = 8m/s
C
torque [Nm]
0.4 C u1 = 4m/s
cp(!)
Trated power
D
Tcpmax
0.2
D
B
0.0
12 A Aω
0 4
!
8
u1min !
0
Michael Hölling, WS 2010/2011 slide 26

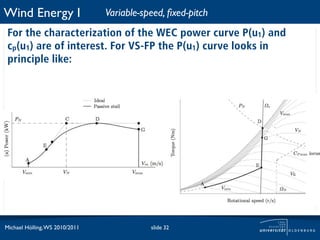
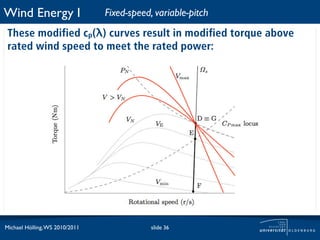
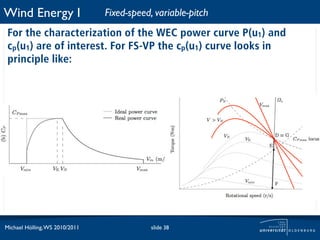
27. Wind Energy I Fixed-speed, fixed-pitch
For the characterization of the WEC power curve P(u1) and
cp(u1) are of interest. For FS-FP the P(u1) curve looks in principle
like:
C
u1 = 17m/s
D
u1max u1 = 8m/s
torque [Nm]
P(u1)/Prated
C u1 = 4m/s
Trated power
D
Tcpmax
B
ideal power curve B
power curve
A5 Aω
0 10 15 20 25 30
u1min !
0
u1 [m/s]
Michael Hölling, WS 2010/2011 slide 27

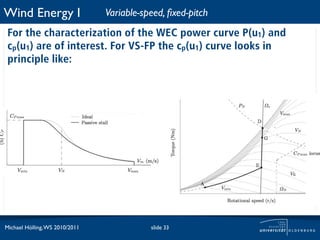
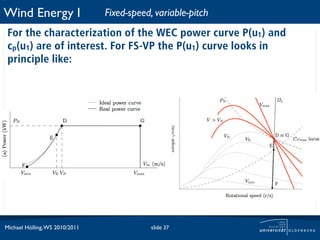
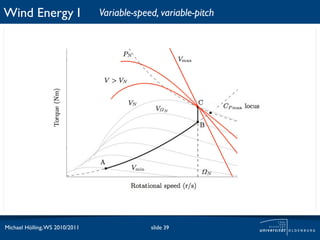
28. Wind Energy I Fixed-speed, fixed-pitch
For the characterization of the WEC power curve P(u1) and
cp(u1) are of interest. For FS-FP the cp(u1) curve looks in
principle like:
B u1 = 17m/s
u1max u1 = 8m/s
torque [Nm]
C u1 = 4m/s
cp(u1)
C Trated power
D
Tcpmax
ideal cp
real cp D B
A Aω
0 5 10 15 20 25 30
u1min !
0
u1 [m/s]
Michael Hölling, WS 2010/2011 slide 28

29. Wind Energy I Fixed-speed, fixed-pitch
Power regulation by passive stall
Michael Hölling, WS 2010/2011 slide 29

30. Wind Energy I Variable-speed, fixed-pitch
For a variable-speed, fixed.pitch machine the rotational speed
ωrot can be adapted to meet the optimum tip speed ratio λ0.
λ0 · u1
ωrot =
R
The rotational speed ωrot changes linearly with the ambient
wind speed u1.
This is applied in the region below rated wind speed.
Michael Hölling, WS 2010/2011 slide 30

31. Wind Energy I Variable-speed, fixed-pitch
Variable rotational-speed ωrot is realized by adding AC/DC-DC/
AC converter before feeding into the grid.
0.6
A-E cp(!)
0.4
D
cp(!)
0.2
G
0.0
0 4 8 12
!
Michael Hölling, WS 2010/2011 slide 31

32. Wind Energy I Variable-speed, fixed-pitch
For the characterization of the WEC power curve P(u1) and
cp(u1) are of interest. For VS-FP the P(u1) curve looks in
principle like:
Michael Hölling, WS 2010/2011 slide 32

33. Wind Energy I Variable-speed, fixed-pitch
For the characterization of the WEC power curve P(u1) and
cp(u1) are of interest. For VS-FP the cp(u1) curve looks in
principle like:
Michael Hölling, WS 2010/2011 slide 33

34. Wind Energy I Fixed-speed, variable-pitch
There are two different ways to adjust the pitch to keep the
power above rated wind speed constant:
pitch to feather pitch to stall
Michael Hölling, WS 2010/2011 slide 34

35. Wind Energy I Fixed-speed, variable-pitch
By adjusting the angle of attack the cp(λ) curves are different
for each pitch angle:
tip speed ratio
Michael Hölling, WS 2010/2011 slide 35

36. Wind Energy I Fixed-speed, variable-pitch
These modified cp(λ) curves result in modified torque above
rated wind speed to meet the rated power:
Michael Hölling, WS 2010/2011 slide 36

37. Wind Energy I Fixed-speed, variable-pitch
For the characterization of the WEC power curve P(u1) and
cp(u1) are of interest. For FS-VP the P(u1) curve looks in
principle like:
Michael Hölling, WS 2010/2011 slide 37

38. Wind Energy I Fixed-speed, variable-pitch
For the characterization of the WEC power curve P(u1) and
cp(u1) are of interest. For FS-VP the cp(u1) curve looks in
principle like:
Michael Hölling, WS 2010/2011 slide 38

39. Wind Energy I Variable-speed, variable-pitch
Michael Hölling, WS 2010/2011 slide 39