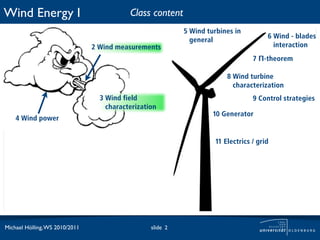
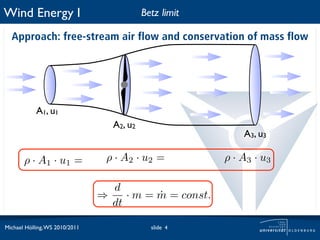
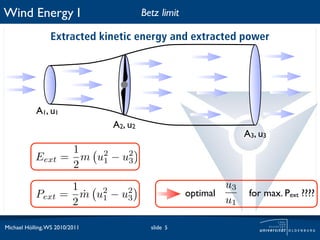
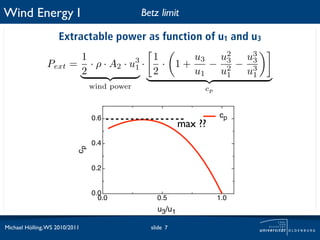
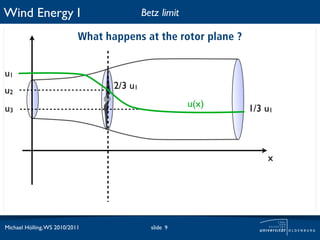
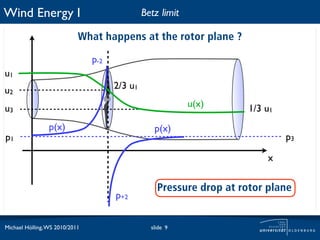
The document discusses the theoretical maximum efficiency of a wind turbine, known as the Betz limit. It presents the derivation of the Betz limit through analysis of the conservation of mass flow and kinetic energy extraction as air passes through a turbine. The derivation shows that the maximum possible power coefficient is 59% when the downstream wind speed is 1/3 of the upstream speed. This optimal ratio is characterized by the tip speed ratio. The document also notes that in practice, the power coefficient of a wind turbine is typically around 40-60% of the theoretical maximum depending on wind speed.

1. Wind Energy I
Wind power
Michael Hölling, WS 2010/2011 slide 1

2. Wind Energy I Class content
5 Wind turbines in
6 Wind - blades
general
2 Wind measurements interaction
7 Π-theorem
8 Wind turbine
characterization
3 Wind field 9 Control strategies
characterization
10 Generator
4 Wind power
11 Electrics / grid
Michael Hölling, WS 2010/2011 slide 2

3. Wind Energy I Motivation
How much power can be extracted from the wind ?
Michael Hölling, WS 2010/2011 slide 3

4. Wind Energy I Betz limit
Approach: free-stream air flow and conservation of mass flow
A1, u1
A2, u2
A3, u3
ρ · A1 · u 1 = ρ · A2 · u 2 = ρ · A3 · u 3
d
⇒ · m = m = const.
˙
dt
Michael Hölling, WS 2010/2011 slide 4

5. Wind Energy I Betz limit
Extracted kinetic energy and extracted power
A1, u1
A2, u2
A3, u3
1
Eext = m u1 − u3
2 2
2
1 u3
Pext = m u2 − u2
˙ 1 optimal for max. Pext ????
2 3 u1
Michael Hölling, WS 2010/2011 slide 5

6. Wind Energy I Betz limit
Substitution of u2 will lead to a function Pext(u1,u3)
1
Pext = · ρ · A2 · u 2 · u 1 − u 3
2 2
2
has to be substituted
Thrust: T = m (u1 − u3 )
˙
Corresponding power: Pthrust = m (u1 − u3 ) · u2
˙
Equals mechanical power 1
that can be extracted: Pmech = Pext = m u2 − u2
˙ 1 3
2
u1 + u2
⇒ u2 =
2
Michael Hölling, WS 2010/2011 slide 6

7. Wind Energy I Betz limit
Extractable power as function of u1 and u3
1 1 u3 u2 u3
Pext = · ρ · A2 · u 1 ·
3
· 1+ 3 3
− 2− 3
2 2 u1 u1 u1
wind power cp
0.6 cp
max ??
0.4
cp
0.2
0.0
0.0 0.5 1.0
u3/u1
Michael Hölling, WS 2010/2011 slide 7

8. Wind Energy I Betz limit
Find the maximum cp by taking the first derivative
1
Substitute u3/u1 with x: cp (x) = · 1 + x − x − x
2 3
2
1 !
First derivative of cp(x): cp (x) = · 1 − 2x − 3x = 0
2
2
For maximum second derivative of possible solution x1/2
1
must smaller than zero: cp (x1/2 ) = · (−2 − 6x) < 0
2
1 16
Solution: x = ⇒ cpmax. (1/3) = ≈ 59%
3 27
Michael Hölling, WS 2010/2011 slide 8

9. Wind Energy I Betz limit
What happens at the rotor plane ?
u1
u2 2/3 u1
u3 u(x) 1/3 u1
x
Michael Hölling, WS 2010/2011 slide 9

10. Wind Energy I Betz limit
What happens at the rotor plane ?
p-2
u1
u2 2/3 u1
u3 u(x) 1/3 u1
p(x) p(x)
p1 p3
x
Pressure drop at rotor plane
p+2
Michael Hölling, WS 2010/2011 slide 9

11. Wind Energy I Betz limit
What does this results mean for wind energy converter ?
There is an optimal rotational frequency that the blockage
u3 1
results in = , characterized by tip speed ratio λ.
u1 3
Michael Hölling, WS 2010/2011 slide 10

12. Wind Energy I Betz limit
What is the value for cp for a WEC over wind speed ?
1.2 1.2
P(u) / Pr
1.0 1.0 cp(u) / cpmax
cp(u) / cpmax
P(u) / Pr
0.8 0.8
0.6 0.6
0.4 0.4
0.2 0.2
0.0 0.0
0 10 20 30
u [m/s]
Michael Hölling, WS 2010/2011 slide 11