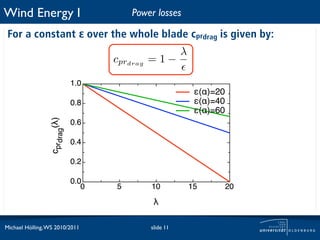
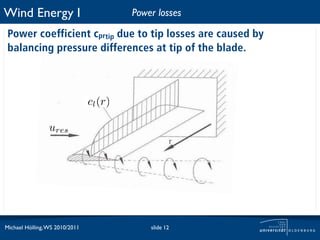
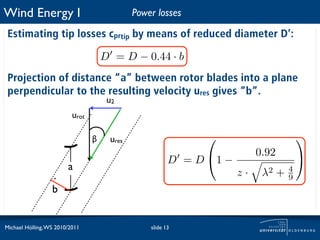
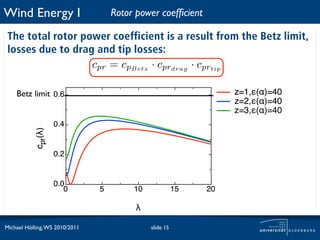
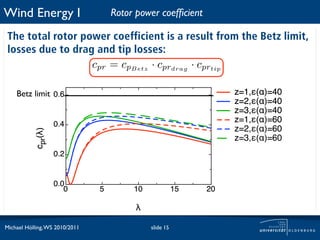
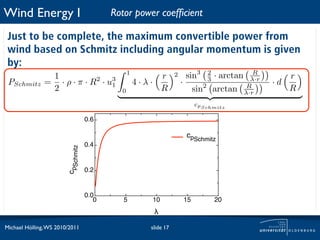
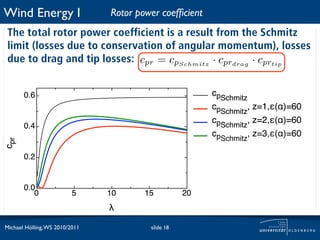
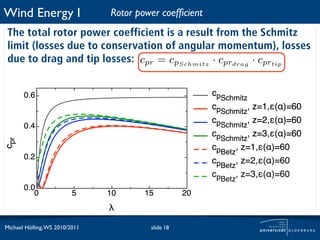
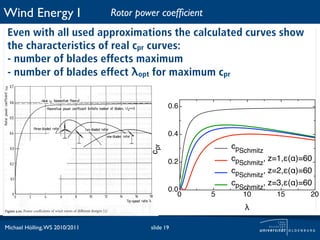
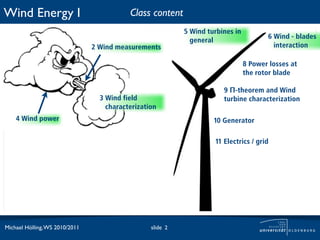
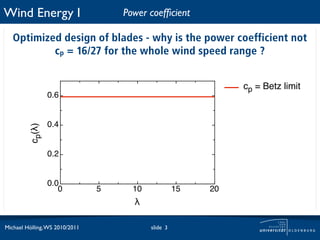
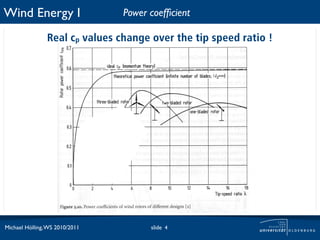
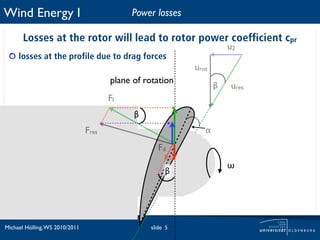
The document discusses power losses that occur at the rotor blades of a wind turbine. It explains that the rotor power coefficient is lower than the theoretical Betz limit due to drag and tip losses. Drag losses are caused by friction on blade surfaces and tip losses occur at the ends of blades due to vortex shedding. The rotor power coefficient can be calculated as the product of coefficients for the Betz limit, drag losses, and tip losses. Graphs show how the different loss coefficients and the total rotor power coefficient vary with tip speed ratio.

1. Wind Energy I
power losses at the
rotor blade
Michael Hölling, WS 2010/2011 slide 1

2. Wind Energy I Class content
5 Wind turbines in
6 Wind - blades
general
2 Wind measurements interaction
8 Power losses at
the rotor blade
9 Π-theorem and Wind
3 Wind field turbine characterization
characterization
4 Wind power 10 Generator
11 Electrics / grid
Michael Hölling, WS 2010/2011 slide 2

3. Wind Energy I Power coefficient
Optimized design of blades - why is the power coefficient not
cp = 16/27 for the whole wind speed range ?
cp = Betz limit
0.6
0.4
cp(!)
0.2
0.0
0 5 10 15 20
!
Michael Hölling, WS 2010/2011 slide 3

4. Wind Energy I Power coefficient
Real cp values change over the tip speed ratio !
Michael Hölling, WS 2010/2011 slide 4

5. Wind Energy I Power losses
Losses at the rotor will lead to rotor power coefficient cpr
u2
losses at the profile due to drag forces
urot
plane of rotation
β ures
Fl
β
Fres α
.
Fd
ω
β
Michael Hölling, WS 2010/2011 slide 5

6. Wind Energy I Power losses
Losses at the rotor will lead to rotor power coefficient cpr
losses at the tip of the blades creates by tip vortices
Michael Hölling, WS 2010/2011 slide 6

7. Wind Energy I Power losses
Determine rotor power coefficient cpr by including losses in
addition to Betz limit - cprdrag and cprtip additional factors:
dProt
cprdrag =
dProtideal
Calculations lead to:
1 3 λ·r
cprdrag =1− · ·
(α) 2 R
Michael Hölling, WS 2010/2011 slide 7

8. Wind Energy I Power losses
Possible behavior of cprdrag over blade radius r for different ε
and λ:
70 1.0
!(r) !=4
!=7
60 ! = 10
0.9
cprdrag(r)
!(r)
50
40 0.8
30 0 10 20 30 40 50
0 10 20 30 40 50
r [m] r [m]
Michael Hölling, WS 2010/2011 slide 8

9. Wind Energy I Power losses
For a ring-segment:
16 1
dPBetz = · · ρ · u1 · (2 · π · r · dr)
3
27 2
dA
r
For just the circumference of a circle:
16 1
dPBetz = · · ρ · u1 · (2 · π · r · dr)
3
27 2
dA
Michael Hölling, WS 2010/2011 slide 10

10. Wind Energy I Power losses
For a constant ε over the whole blade cprdrag is given by:
λ
cprdrag = 1 −
1.0
"(#)=20
0.8 "(#)=40
"(#)=60
cprdrag(!)
0.6
0.4
0.2
0.0
0 5 10 15 20
!
Michael Hölling, WS 2010/2011 slide 11

11. Wind Energy I Power losses
Power coefficient cprtip due to tip losses are caused by
balancing pressure differences at tip of the blade.
cl (r)
ures
Michael Hölling, WS 2010/2011 slide 12

12. Wind Energy I Power losses
Estimating tip losses cprtip by means of reduced diameter D’:
D = D − 0.44 · b
Projection of distance “a” between rotor blades into a plane
perpendicular to the resulting velocity ures gives “b”.
u2
urot
β ures  
0.92
D = D 1 − 
a
. z· λ2 + 4
9
b
Michael Hölling, WS 2010/2011 slide 13

13. Wind Energy I Power losses
 2
0.92
cprtip = 1 − 
z· λ2 + 4
9
1.0
0.8
cprtip(!)
0.6
0.4 z=1
z=2
0.2 z=3
0.0
0 5 10 15 20
!
Michael Hölling, WS 2010/2011 slide 14

14. Wind Energy I Rotor power coefficient
The total rotor power coefficient is a result from the Betz limit,
losses due to drag and tip losses:
cpr = cpBetz · cprdrag · cprtip
Betz limit 0.6 z=1,"(#)=40
z=2,"(#)=40
z=3,"(#)=40
0.4
cpr(!)
0.2
0.0
0 5 10 15 20
!
Michael Hölling, WS 2010/2011 slide 15

15. Wind Energy I Rotor power coefficient
The total rotor power coefficient is a result from the Betz limit,
losses due to drag and tip losses:
cpr = cpBetz · cprdrag · cprtip
Betz limit 0.6 z=1,"(#)=40
z=2,"(#)=40
z=3,"(#)=40
0.4
z=1,"(#)=60
z=2,"(#)=60
cpr(!)
z=3,"(#)=60
0.2
0.0
0 5 10 15 20
!
Michael Hölling, WS 2010/2011 slide 15

16. Wind Energy I Rotor power coefficient
Maximum convertible power from wind based on Schmitz (and
Gaulert) including conservation angular momentum:
“Based on the conservation of angular momentum, if the rotor gains angular momentum from the linear wind
stream, then there must be some compensation, which is in the form of an opposite rotating wake, so that the
overall angular momentum does not change. ”
Michael Hölling, WS 2010/2011 slide 16

17. Wind Energy I Rotor power coefficient
Just to be complete, the maximum convertible power from
wind based on Schmitz including angular momentum is given
by:
1 1
r 2 sin3 2
· arctan R
r
PSchmitz = · ρ · π · R 2 · u3 4·λ· · 3 λ·r
·d
2 1
0 R sin2 arctan R
λ·r
R
cpSchmitz
0.6
cpSchmitz
0.4
cpSchmitz
0.2
0.0
0 5 10 15 20
!
Michael Hölling, WS 2010/2011 slide 17

18. Wind Energy I Rotor power coefficient
The total rotor power coefficient is a result from the Schmitz
limit (losses due to conservation of angular momentum), losses
due to drag and tip losses: cpr = cpSchmitz · cprdrag · cprtip
0.6 cpSchmitz
cpSchmitz, z=1,"(#)=60
cpSchmitz, z=2,"(#)=60
0.4
cpSchmitz, z=3,"(#)=60
cpr
0.2
0.0
0 5 10 15 20
!
Michael Hölling, WS 2010/2011 slide 18

19. Wind Energy I Rotor power coefficient
The total rotor power coefficient is a result from the Schmitz
limit (losses due to conservation of angular momentum), losses
due to drag and tip losses: cpr = cpSchmitz · cprdrag · cprtip
0.6 cpSchmitz
cpSchmitz, z=1,"(#)=60
cpSchmitz, z=2,"(#)=60
0.4
cpSchmitz, z=3,"(#)=60
cpr
cpBetz, z=1,"(#)=60
0.2
cpBetz, z=2,"(#)=60
cpBetz, z=3,"(#)=60
0.0
0 5 10 15 20
!
Michael Hölling, WS 2010/2011 slide 18

20. Wind Energy I Rotor power coefficient
Even with all used approximations the calculated curves show
the characteristics of real cpr curves:
- number of blades effects maximum
- number of blades effect λopt for maximum cpr
0.6
0.4
cpSchmitz
cpr cpSchmitz, z=1,"(#)=60
0.2
cpSchmitz, z=2,"(#)=60
cpSchmitz, z=3,"(#)=60
0.0
0 5 10 15 20
!
Michael Hölling, WS 2010/2011 slide 19

21. Wind Energy I Blade optimization - Schmitz
Chord length optimization based on Schmitz limit in
comparison to Betz limit:
Michael Hölling, WS 2010/2011 slide 20

22. Wind Energy I Blade optimization - Schmitz
blade twist optimization based on Schmitz limit in comparison
to Betz limit::
Michael Hölling, WS 2010/2011 slide 21