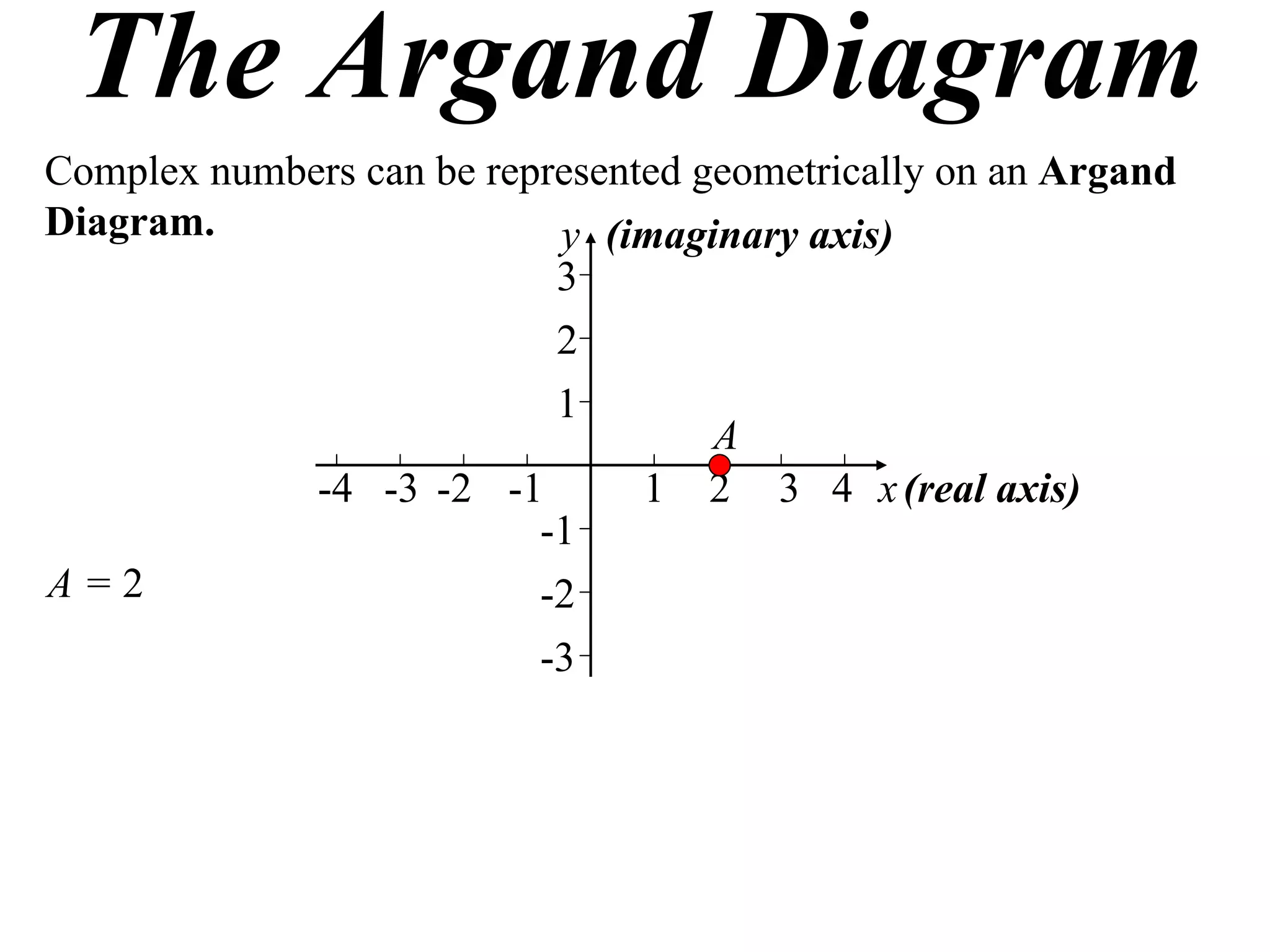
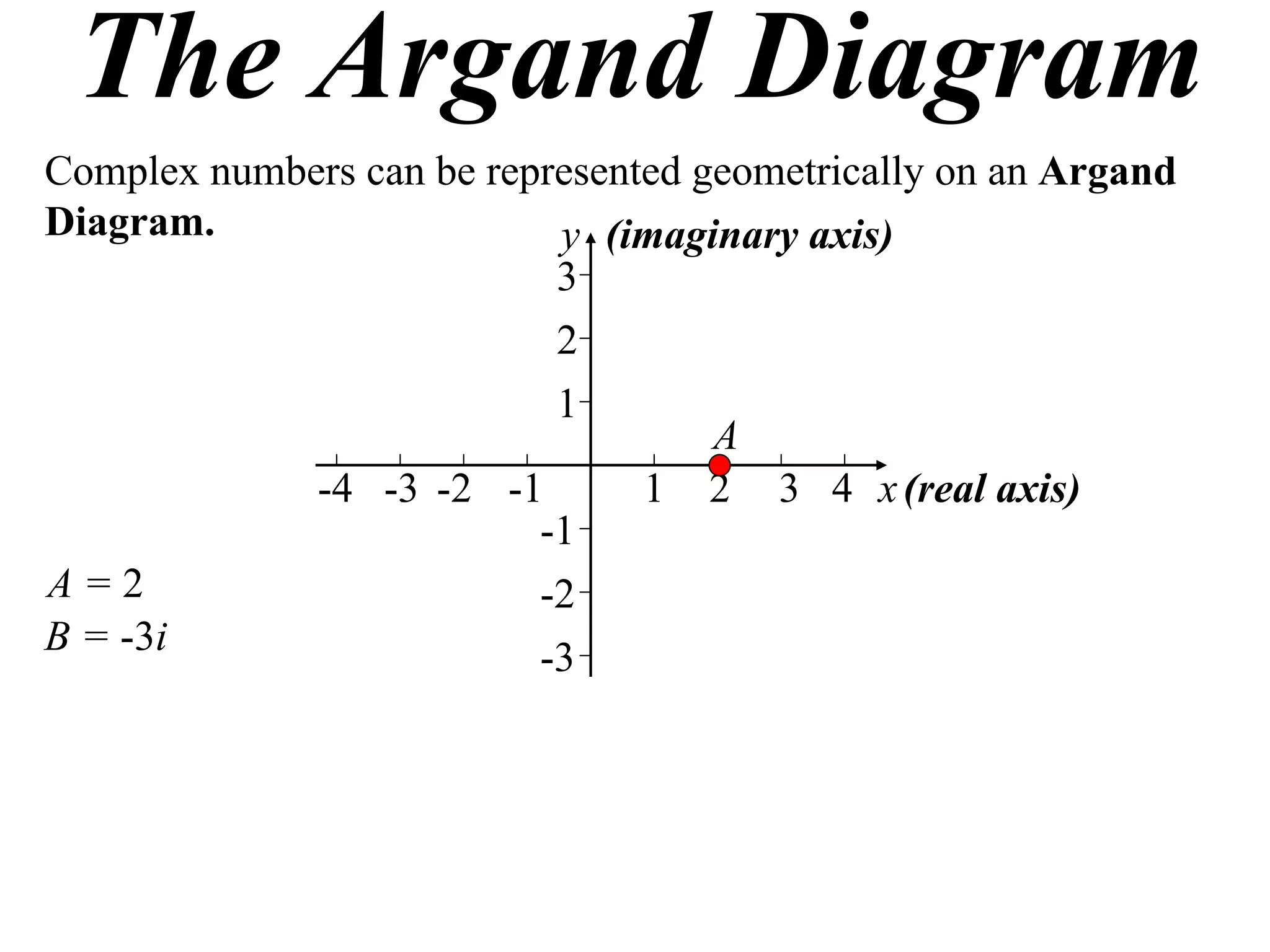
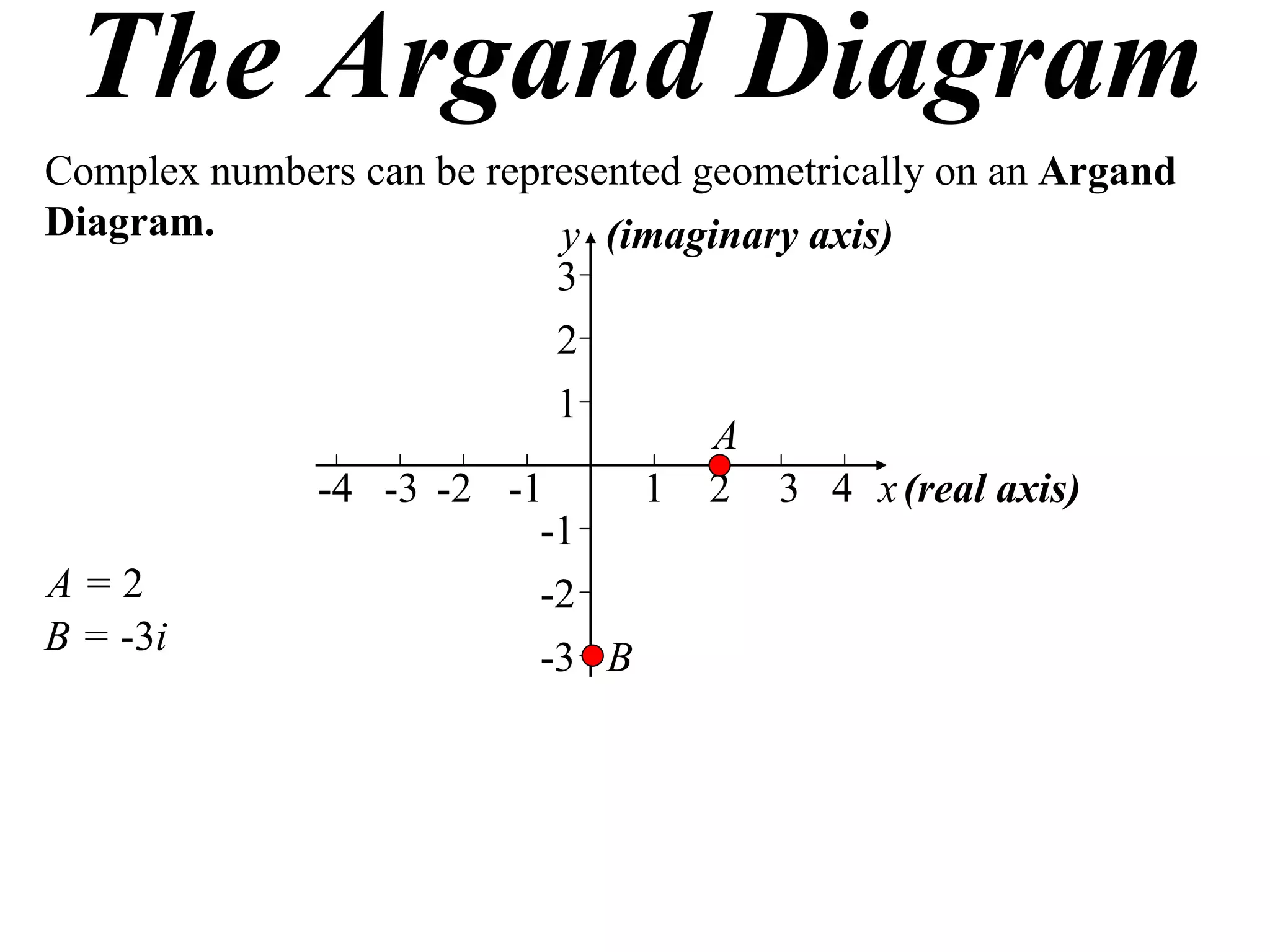
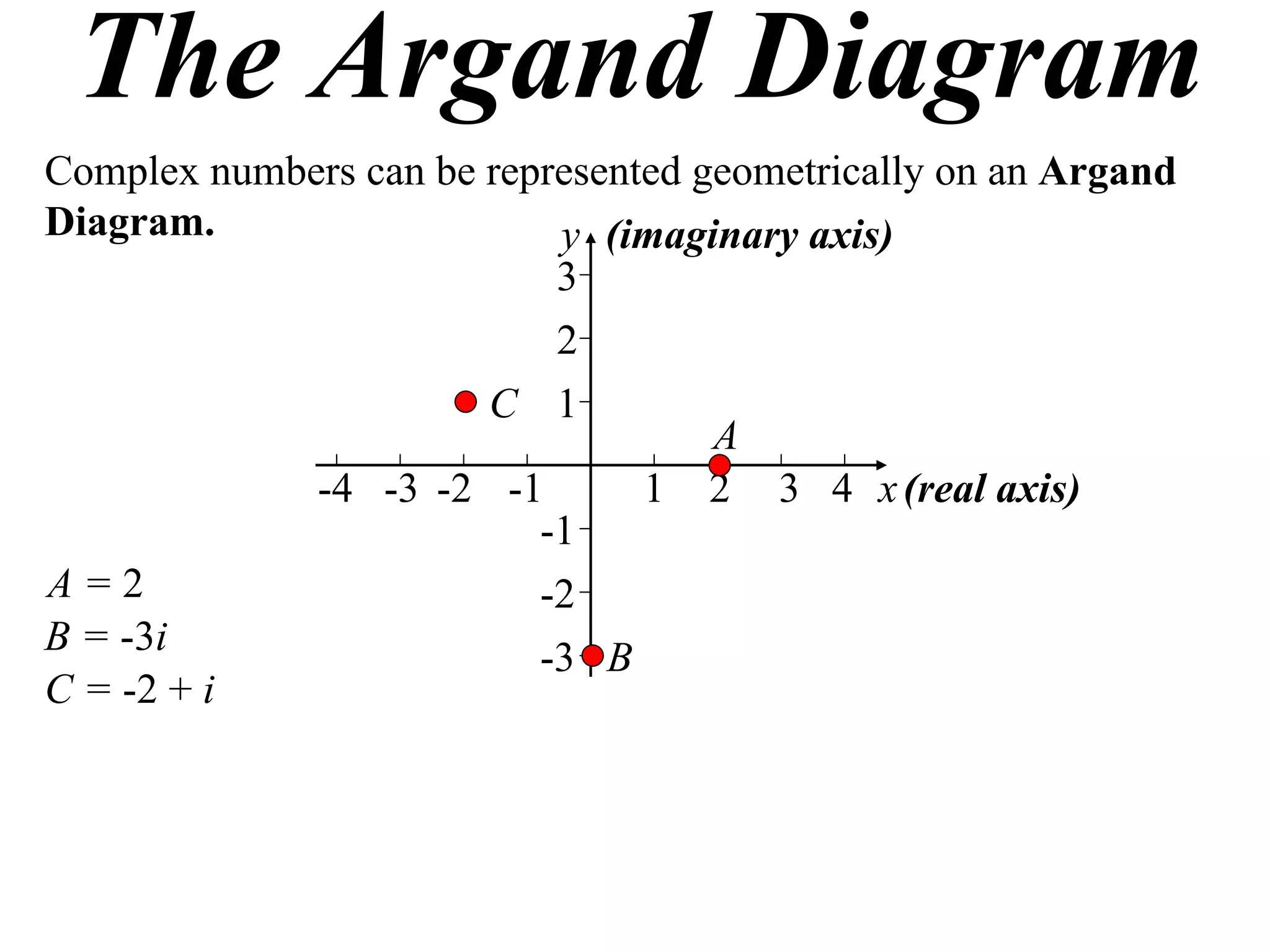
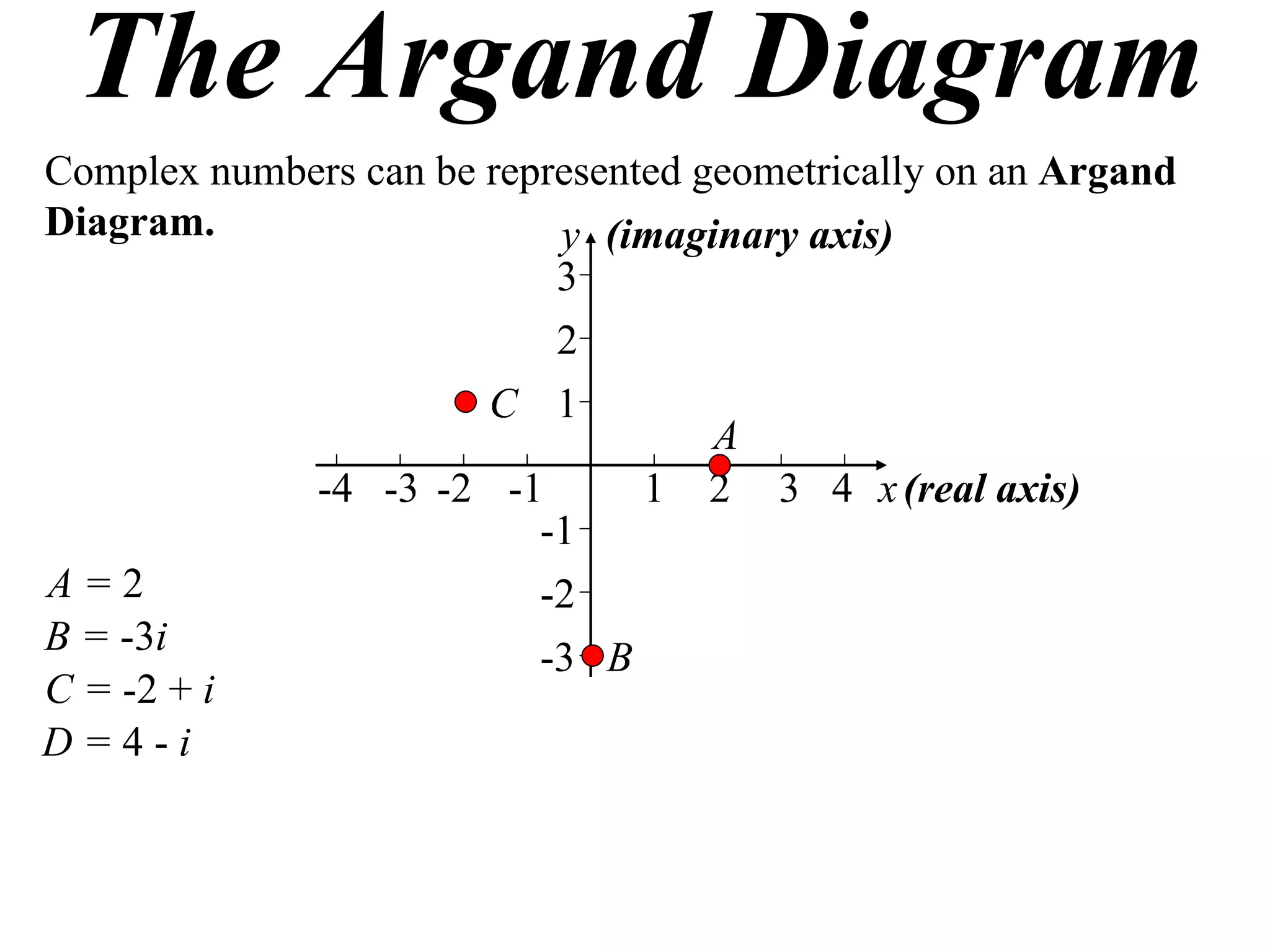
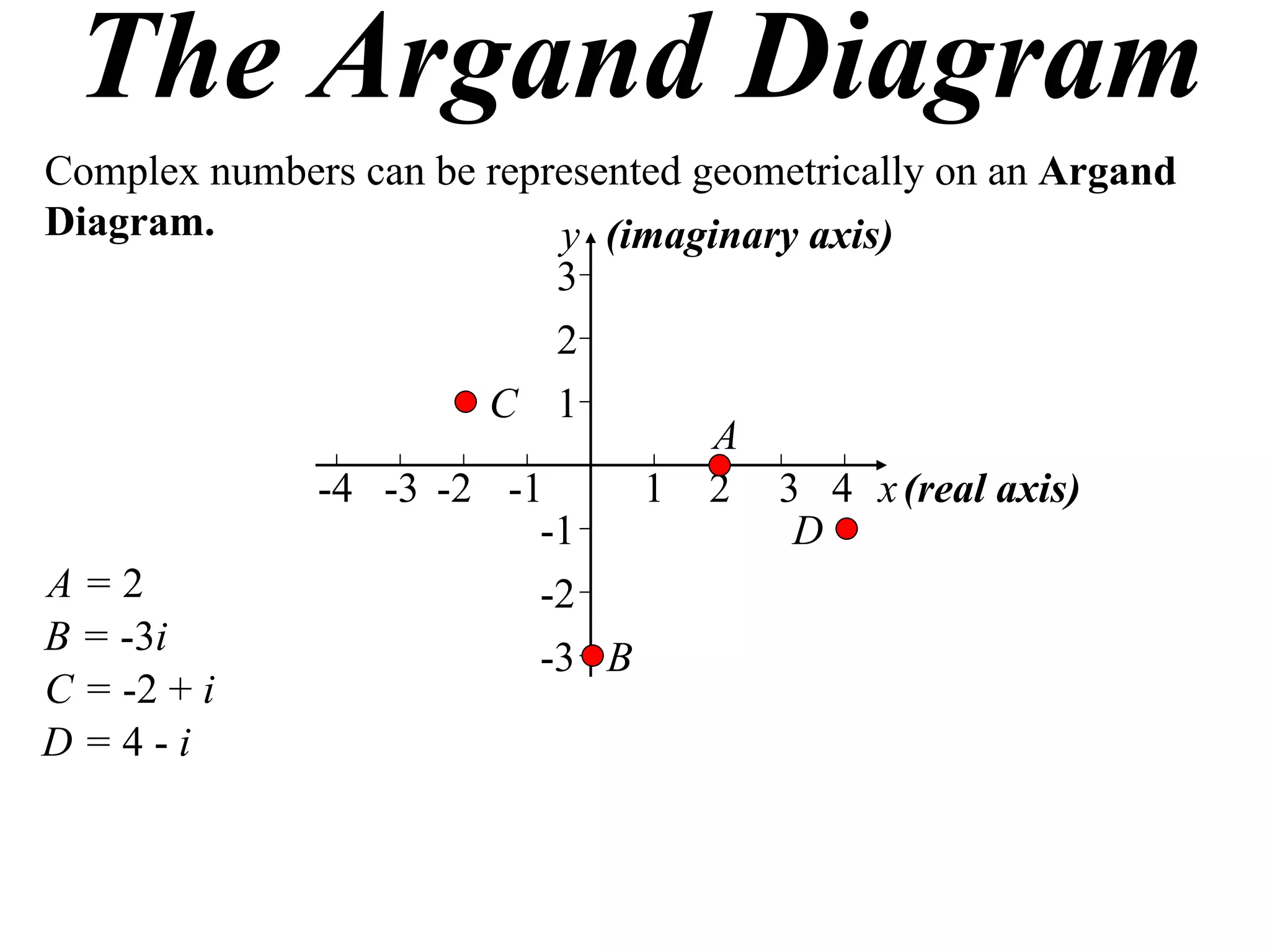
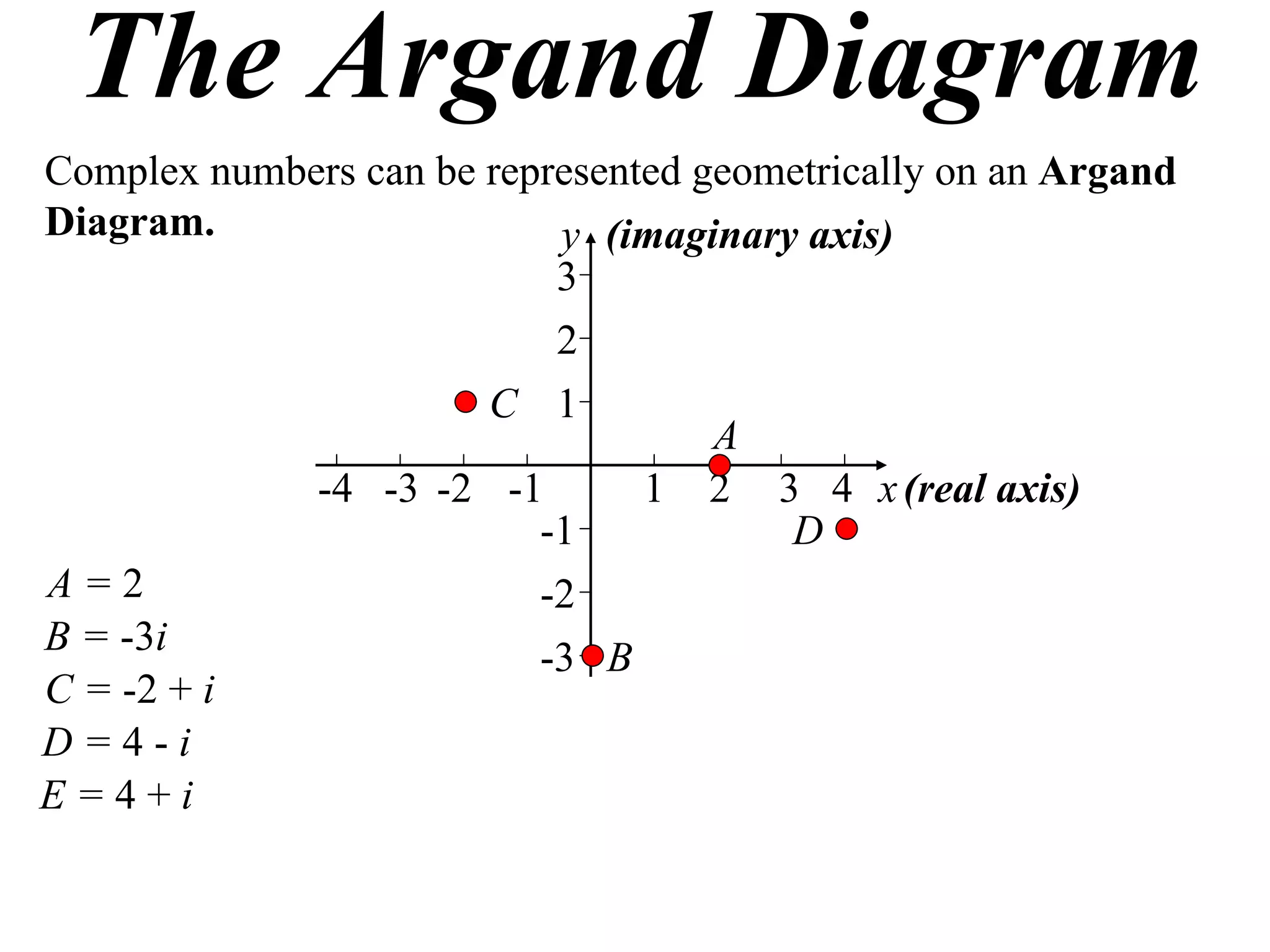
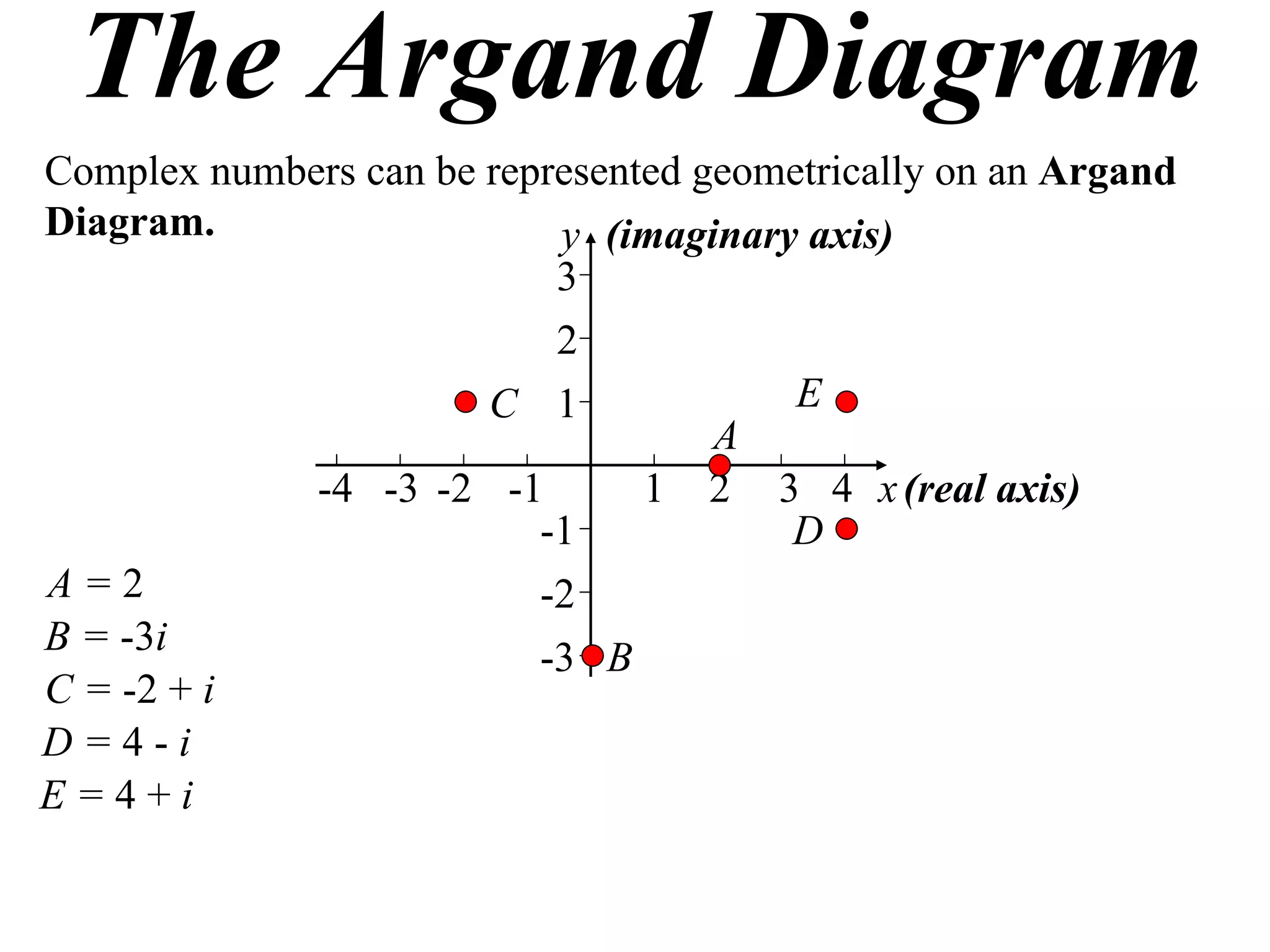
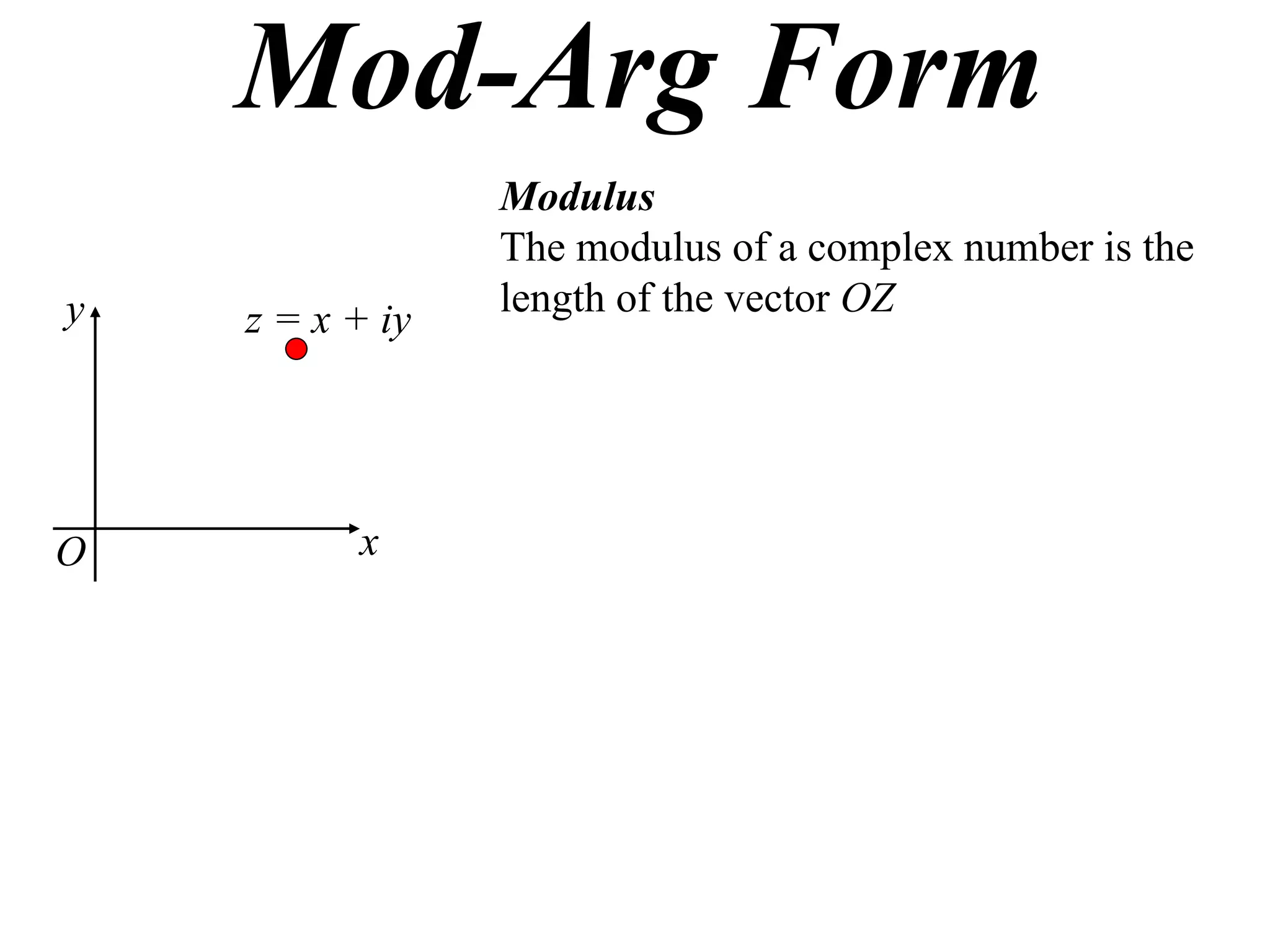
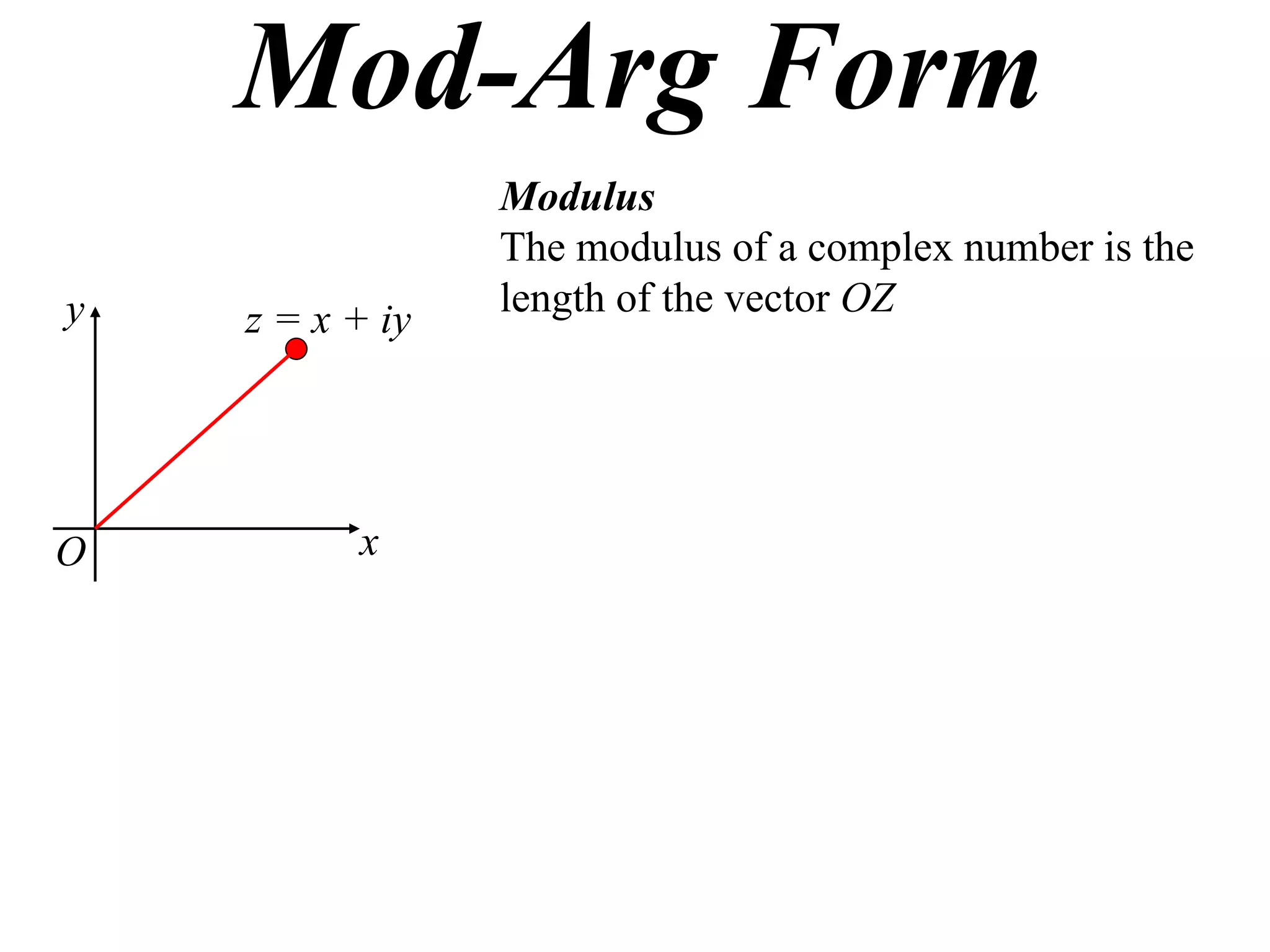
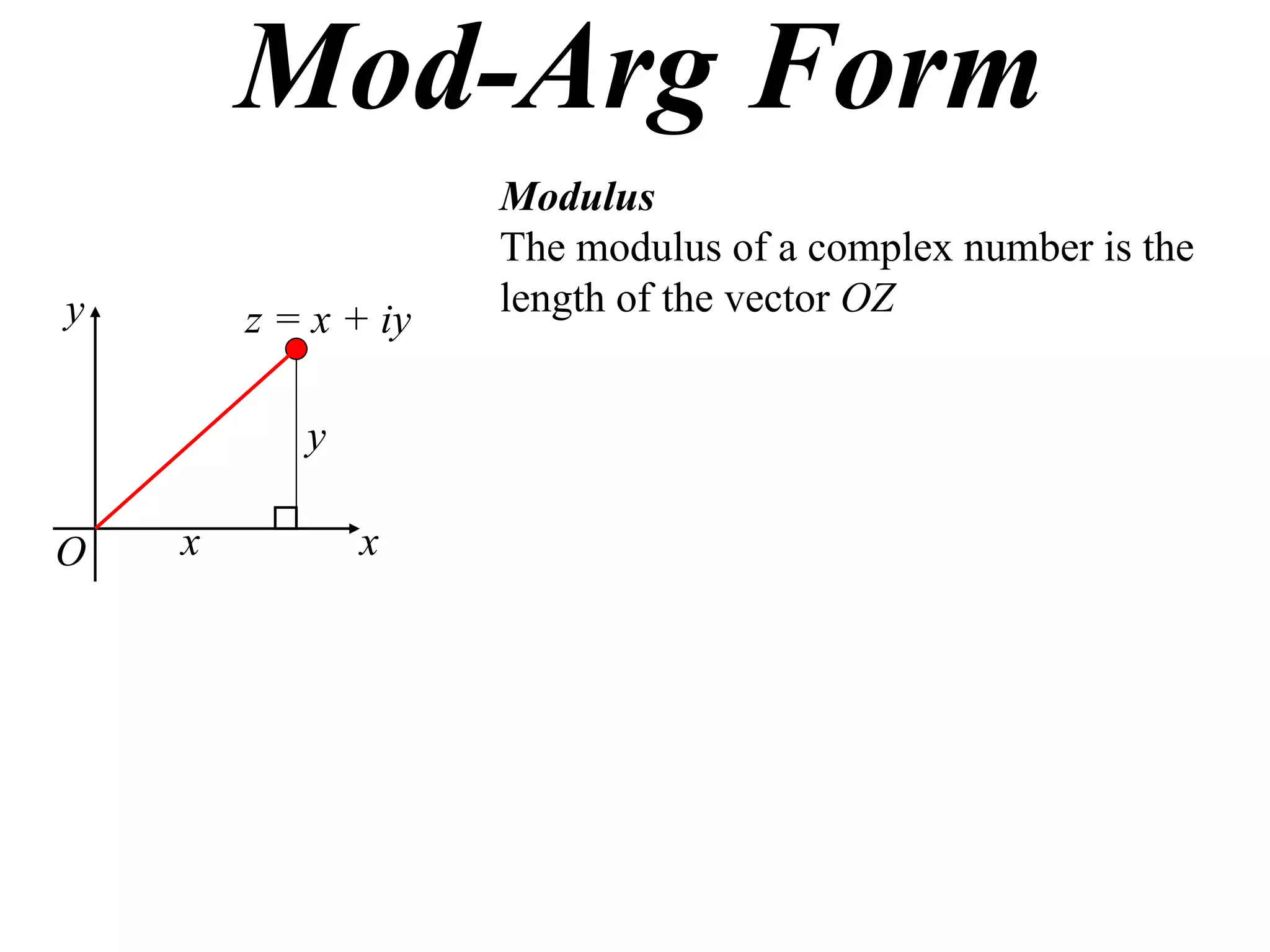
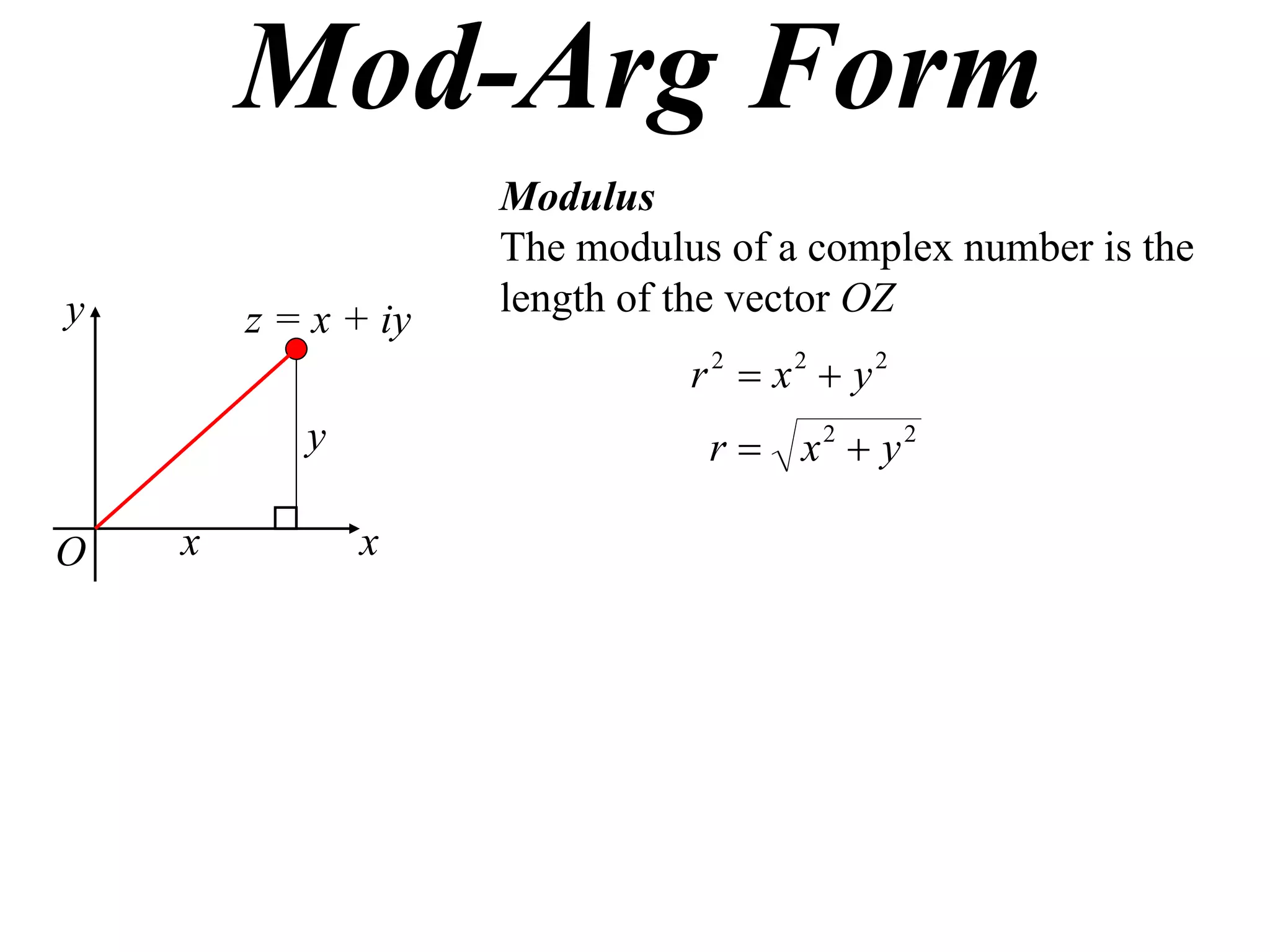
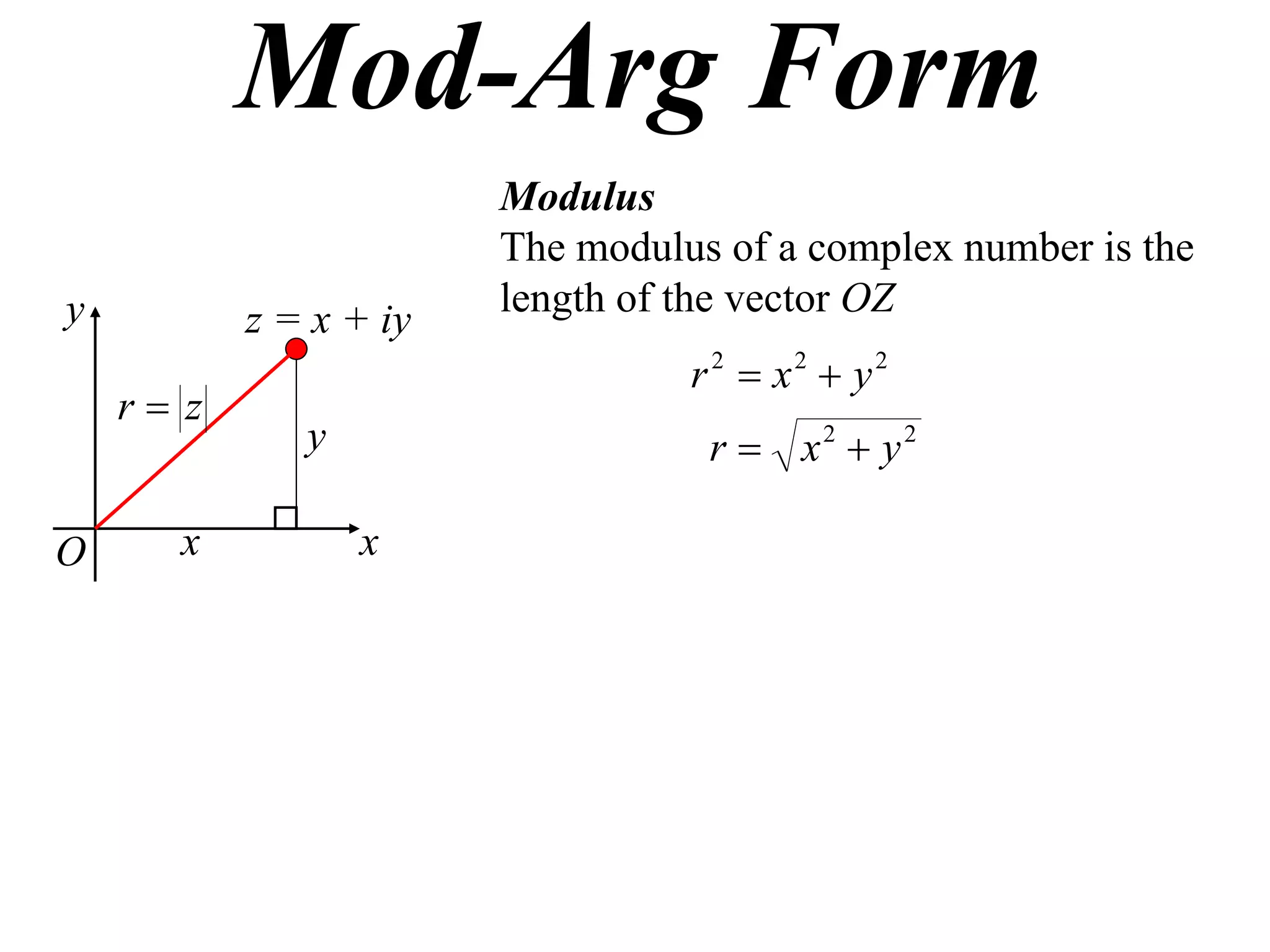
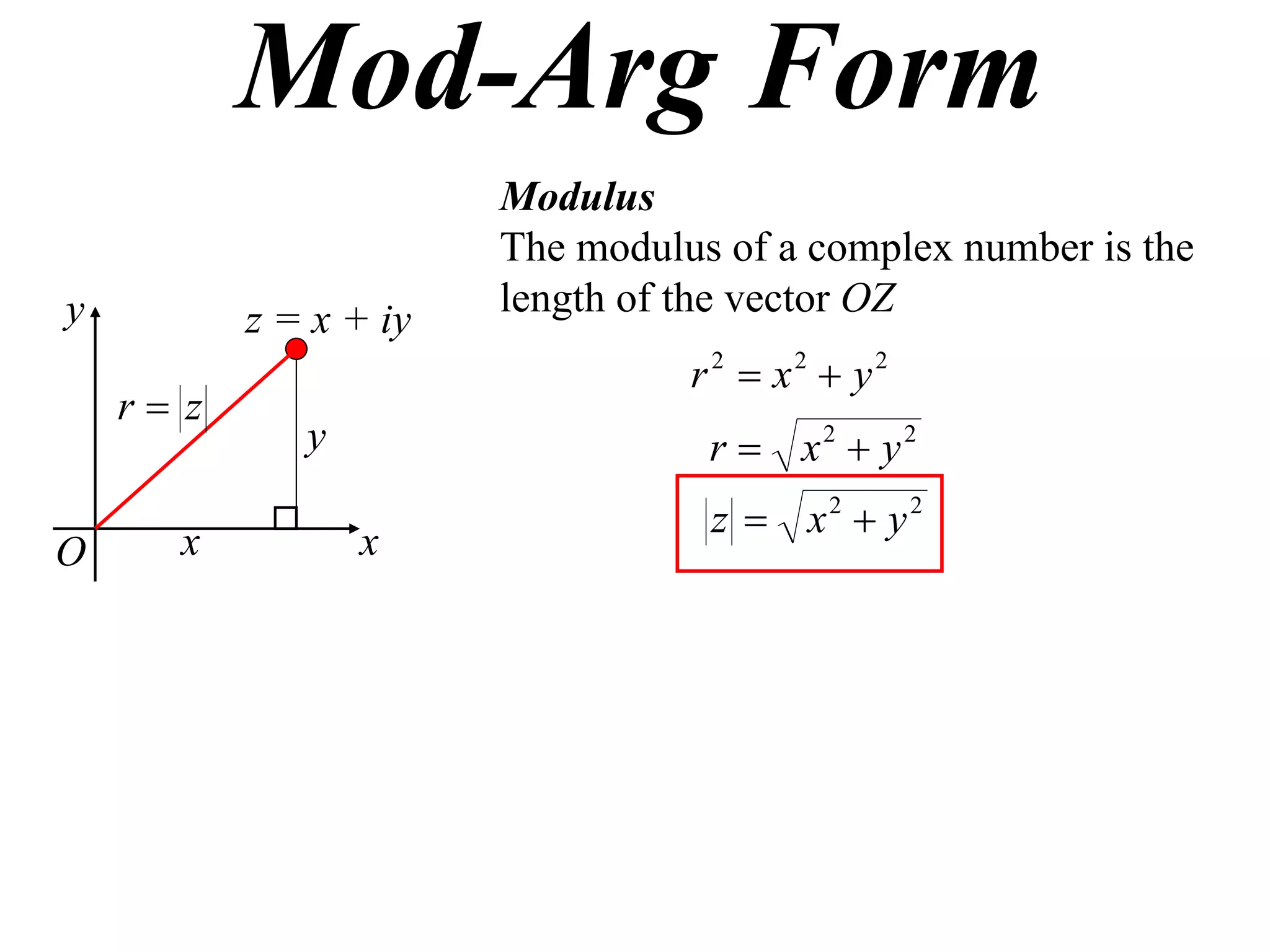
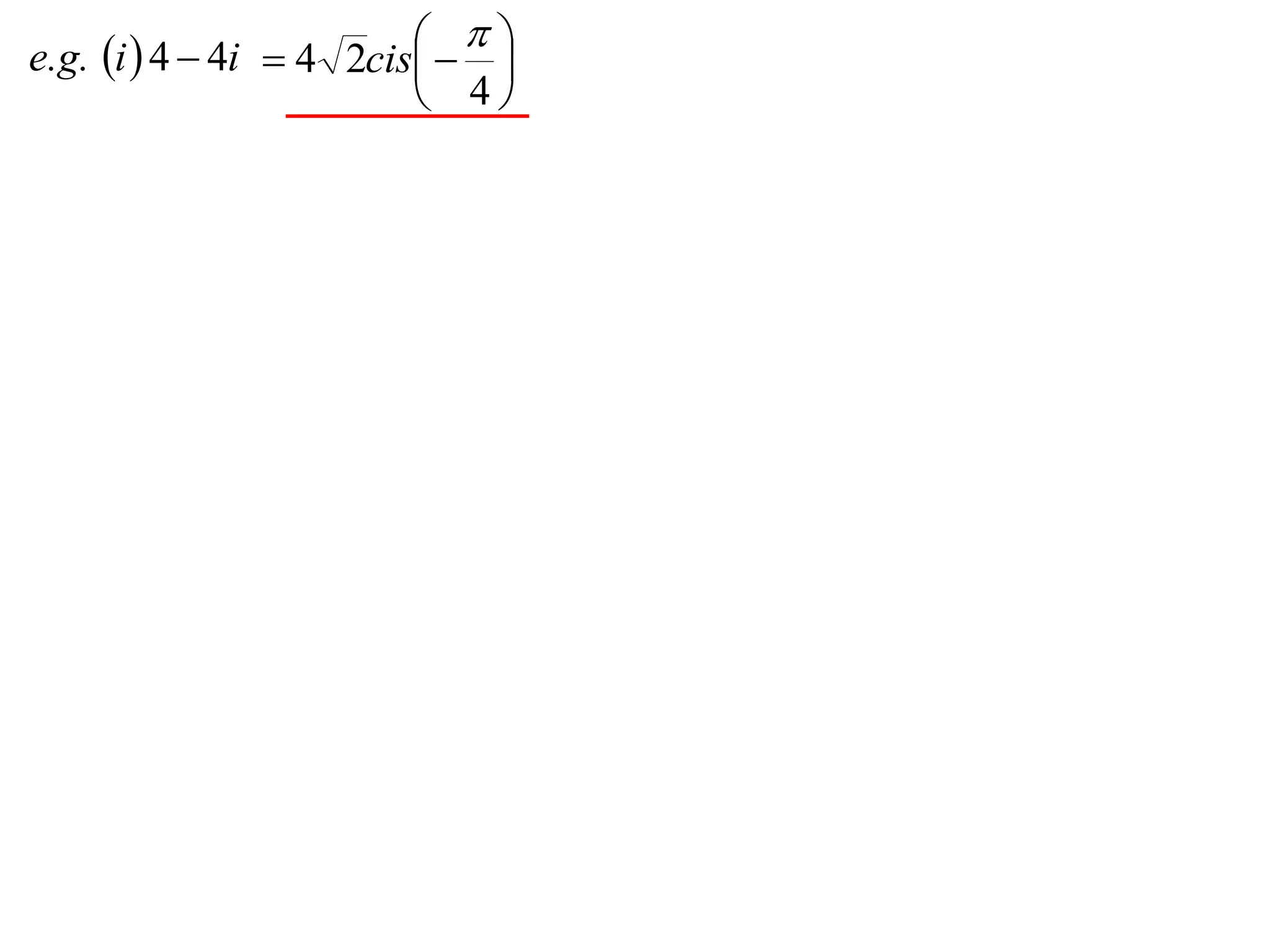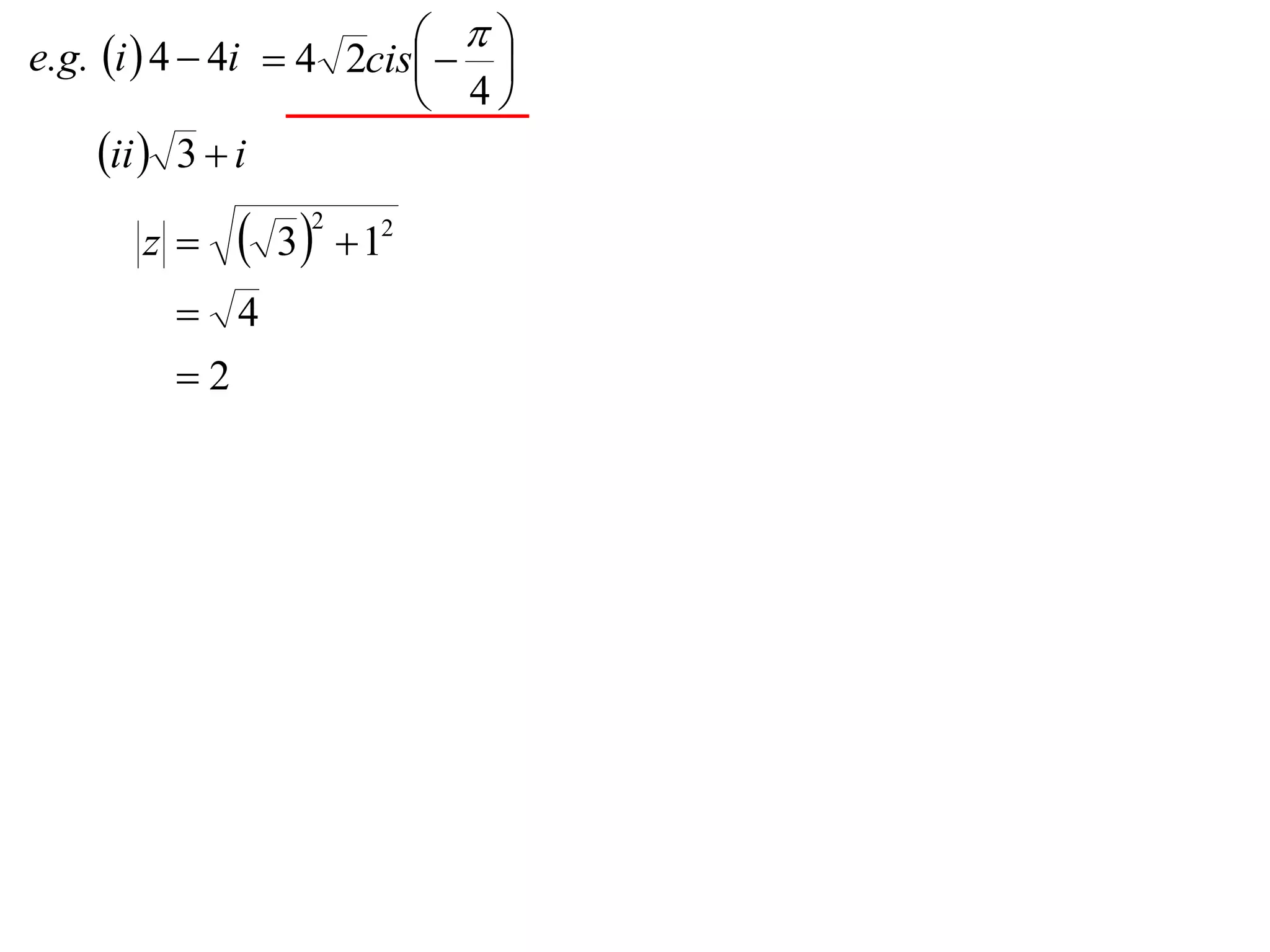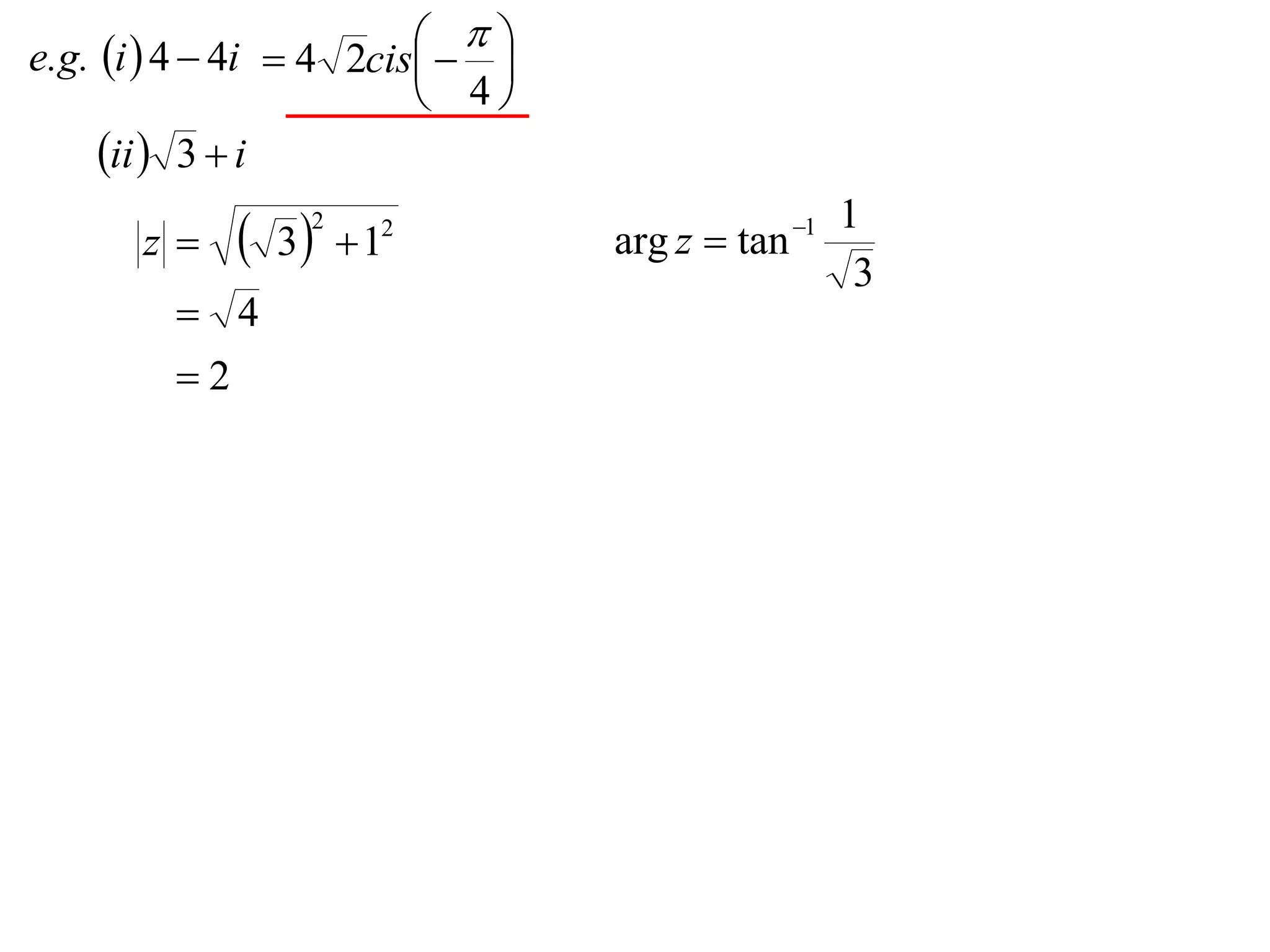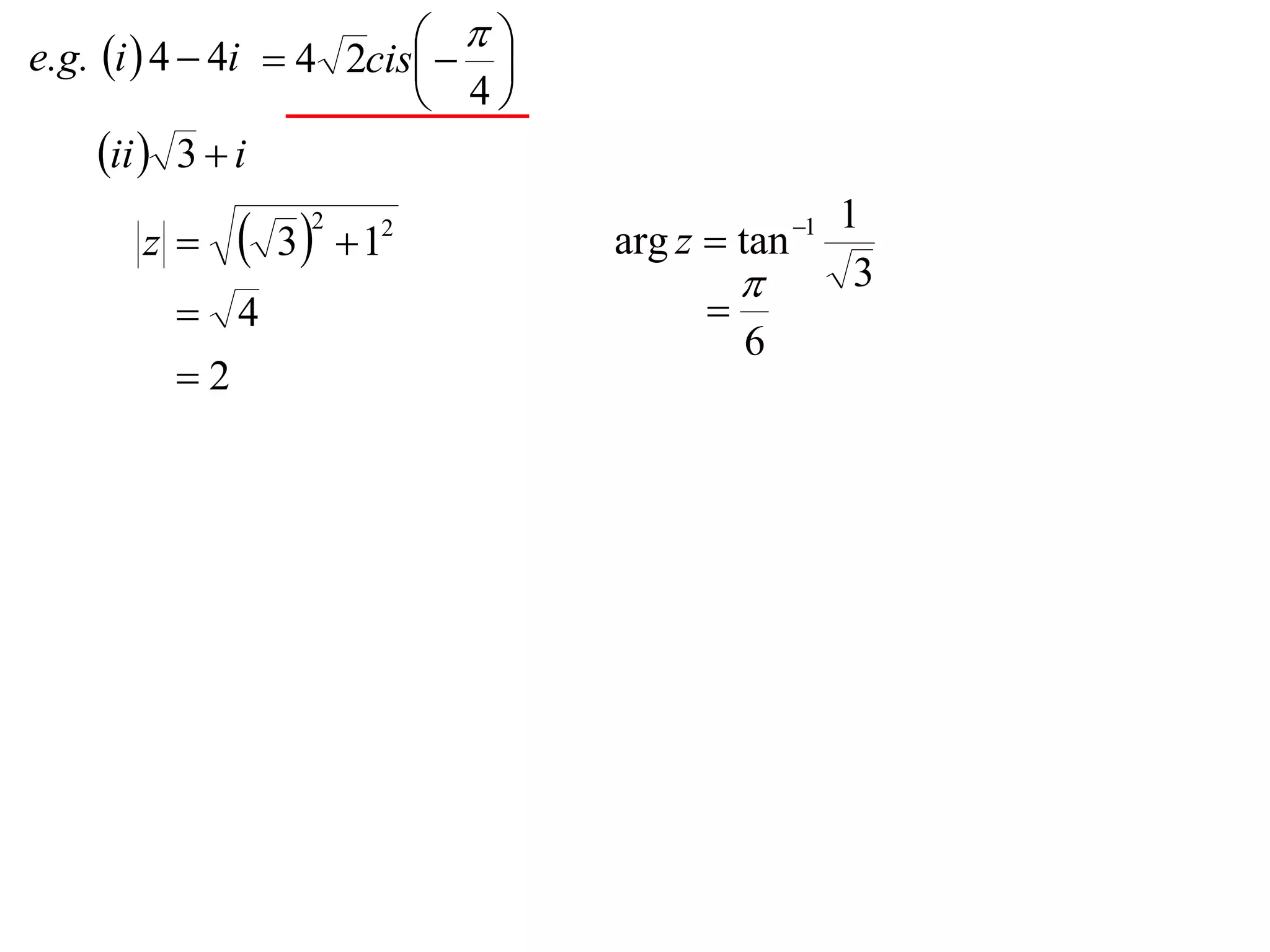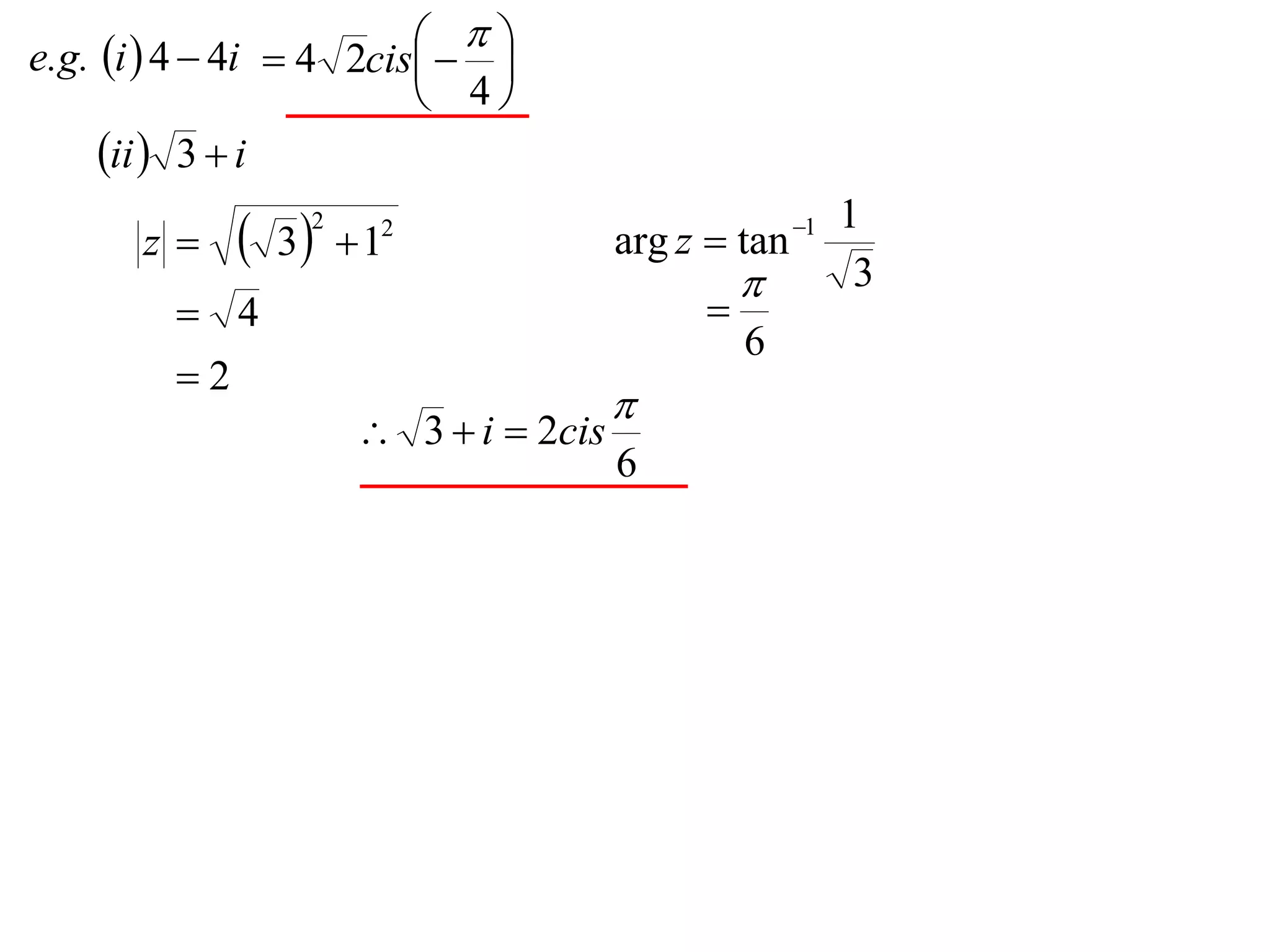The document describes how complex numbers can be represented geometrically using an Argand diagram. The Argand diagram plots the real component of a complex number along the x-axis and the imaginary component along the y-axis, allowing any complex number to be represented as a point in the diagram. The document also explains how every complex number can be expressed in terms of its modulus and argument, where the modulus is the distance from the origin to the point and the argument is the angle relative to the positive real axis. An example of finding the modulus and argument of a complex number is provided.

1. The Argand Diagram

2. The Argand Diagram
Complex numbers can be represented geometrically on an Argand
Diagram.

3. The Argand Diagram
Complex numbers can be represented geometrically on an Argand
Diagram. y
3
2
1
-4 -3 -2 -1 1 2 3 4 x
-1
-2
-3

4. The Argand Diagram
Complex numbers can be represented geometrically on an Argand
Diagram. y
3
2
1
-4 -3 -2 -1 1 2 3 4 x (real axis)
-1
-2
-3

5. The Argand Diagram
Complex numbers can be represented geometrically on an Argand
Diagram. y (imaginary axis)
3
2
1
-4 -3 -2 -1 1 2 3 4 x (real axis)
-1
-2
-3

6. The Argand Diagram
Complex numbers can be represented geometrically on an Argand
Diagram. y (imaginary axis)
3
2
1
-4 -3 -2 -1 1 2 3 4 x (real axis)
-1
A=2 -2
-3

7. The Argand Diagram
Complex numbers can be represented geometrically on an Argand
Diagram. y (imaginary axis)
3
2
1
A
-4 -3 -2 -1 1 2 3 4 x (real axis)
-1
A=2 -2
-3

8. The Argand Diagram
Complex numbers can be represented geometrically on an Argand
Diagram. y (imaginary axis)
3
2
1
A
-4 -3 -2 -1 1 2 3 4 x (real axis)
-1
A=2 -2
B = -3i -3

9. The Argand Diagram
Complex numbers can be represented geometrically on an Argand
Diagram. y (imaginary axis)
3
2
1
A
-4 -3 -2 -1 1 2 3 4 x (real axis)
-1
A=2 -2
B = -3i -3 B

10. The Argand Diagram
Complex numbers can be represented geometrically on an Argand
Diagram. y (imaginary axis)
3
2
1
A
-4 -3 -2 -1 1 2 3 4 x (real axis)
-1
A=2 -2
B = -3i -3 B
C = -2 + i

11. The Argand Diagram
Complex numbers can be represented geometrically on an Argand
Diagram. y (imaginary axis)
3
2
C 1
A
-4 -3 -2 -1 1 2 3 4 x (real axis)
-1
A=2 -2
B = -3i -3 B
C = -2 + i

12. The Argand Diagram
Complex numbers can be represented geometrically on an Argand
Diagram. y (imaginary axis)
3
2
C 1
A
-4 -3 -2 -1 1 2 3 4 x (real axis)
-1
A=2 -2
B = -3i -3 B
C = -2 + i
D=4-i

13. The Argand Diagram
Complex numbers can be represented geometrically on an Argand
Diagram. y (imaginary axis)
3
2
C 1
A
-4 -3 -2 -1 1 2 3 4 x (real axis)
-1 D
A=2 -2
B = -3i -3 B
C = -2 + i
D=4-i

14. The Argand Diagram
Complex numbers can be represented geometrically on an Argand
Diagram. y (imaginary axis)
3
2
C 1
A
-4 -3 -2 -1 1 2 3 4 x (real axis)
-1 D
A=2 -2
B = -3i -3 B
C = -2 + i
D=4-i
E=4+i

15. The Argand Diagram
Complex numbers can be represented geometrically on an Argand
Diagram. y (imaginary axis)
3
2
C 1 E
A
-4 -3 -2 -1 1 2 3 4 x (real axis)
-1 D
A=2 -2
B = -3i -3 B
C = -2 + i
D=4-i
E=4+i

16. The Argand Diagram
Complex numbers can be represented geometrically on an Argand
Diagram. y (imaginary axis)
3 NOTE: Conjugates
2 are reflected in the
C 1 E real (x) axis
A
-4 -3 -2 -1 1 2 3 4 x (real axis)
-1 D
A=2 -2
B = -3i -3 B
C = -2 + i
D=4-i
E=4+i

17. The Argand Diagram
Complex numbers can be represented geometrically on an Argand
Diagram. y (imaginary axis)
3 NOTE: Conjugates
2 are reflected in the
C 1 E real (x) axis
A
-4 -3 -2 -1 1 2 3 4 x (real axis)
-1 D
A=2 -2
B = -3i -3 B
C = -2 + i
D=4-i
E=4+i
Every complex number can be represented by a unique
point on the Argand Diagram.

18. Mod-Arg Form
y
O x

19. Mod-Arg Form
Modulus
The modulus of a complex number is the
y length of the vector OZ
O x

20. Mod-Arg Form
Modulus
The modulus of a complex number is the
y length of the vector OZ
z = x + iy
O x

21. Mod-Arg Form
Modulus
The modulus of a complex number is the
y length of the vector OZ
z = x + iy
O x

22. Mod-Arg Form
Modulus
The modulus of a complex number is the
y length of the vector OZ
z = x + iy
y
O x x

23. Mod-Arg Form
Modulus
The modulus of a complex number is the
y length of the vector OZ
z = x + iy
r 2  x2  y2
y r  x2  y2
O x x

24. Mod-Arg Form
Modulus
The modulus of a complex number is the
y length of the vector OZ
z = x + iy
r 2  x2  y2
r z
y r  x2  y2
O x x

25. Mod-Arg Form
Modulus
The modulus of a complex number is the
y length of the vector OZ
z = x + iy
r 2  x2  y2
r z
y r  x2  y2
z  x2  y2
O x x

26. Mod-Arg Form
Modulus
The modulus of a complex number is the
y length of the vector OZ
z = x + iy
r 2  x2  y2
r z
y r  x2  y2
z  x2  y2
O x x
Argument
The argument of a complex number is
the angle the vector OZ makes with the
positive real (x) axis

27. Mod-Arg Form
Modulus
The modulus of a complex number is the
y length of the vector OZ
z = x + iy
r 2  x2  y2
r z
y r  x2  y2
  arg z z  x2  y2
O x x
Argument
The argument of a complex number is
the angle the vector OZ makes with the
positive real (x) axis

28. Mod-Arg Form
Modulus
The modulus of a complex number is the
y length of the vector OZ
z = x + iy
r 2  x2  y2
r z
y r  x2  y2
  arg z z  x2  y2
O x x
Argument
The argument of a complex number is
the angle the vector OZ makes with the
positive real (x) axis
1 y
arg z  tan  
 x

29. Mod-Arg Form
Modulus
The modulus of a complex number is the
y length of the vector OZ
z = x + iy
r 2  x2  y2
r z
y r  x2  y2
  arg z z  x2  y2
O x x
Argument
The argument of a complex number is
the angle the vector OZ makes with the
positive real (x) axis
 y
1
arg z  tan      arg z  
 x

30. e.g . Find the modulus and argument of 4  4i

31. e.g . Find the modulus and argument of 4  4i
4  4i  4 2   4 
2

32. e.g . Find the modulus and argument of 4  4i
4  4i  4 2   4 
2
 32
4 2

33. e.g . Find the modulus and argument of 4  4i
  4
arg4  4i   tan 
4  4i  4   4 
1

2 2
 4 
 32
4 2

34. e.g . Find the modulus and argument of 4  4i
arg4  4i   tan    4
4  4i  4   4 
1

2 2
 4 
 32  tan 1  1
4 2

35. e.g . Find the modulus and argument of 4  4i
arg4  4i   tan    4
4  4i  4   4 
1

2 2
 4 
 32  tan 1  1
4 2

36. e.g . Find the modulus and argument of 4  4i
arg4  4i   tan    4
4  4i  4   4 
1

2 2
 4 
 32  tan 1  1
4 2 

4

37. e.g . Find the modulus and argument of 4  4i
arg4  4i   tan    4
4  4i  4   4 
1

2 2
 4 
 32  tan 1  1
4 2 

4
Every complex number can be written in terms of its modulus and
argument

38. e.g . Find the modulus and argument of 4  4i
arg4  4i   tan    4
4  4i  4   4 
1

2 2
 4 
 32  tan 1  1
4 2 

4
Every complex number can be written in terms of its modulus and
argument
z  x  iy

39. e.g . Find the modulus and argument of 4  4i
arg4  4i   tan    4
4  4i  4   4 
1

2 2
 4 
 32  tan 1  1
4 2 

4
Every complex number can be written in terms of its modulus and
argument
z  x  iy
 r cos  ir sin 

40. e.g . Find the modulus and argument of 4  4i
arg4  4i   tan    4
4  4i  4   4 
1

2 2
 4 
 32  tan 1  1
4 2 

4
Every complex number can be written in terms of its modulus and
argument
z  x  iy
 r cos  ir sin 
 r cos  i sin  

41. e.g . Find the modulus and argument of 4  4i
arg4  4i   tan    4
4  4i  4   4 
1

2 2
 4 
 32  tan 1  1
4 2 

4
Every complex number can be written in terms of its modulus and
argument
z  x  iy
 r cos  ir sin 
 r cos  i sin  
The mod-arg form of z is;

42. e.g . Find the modulus and argument of 4  4i
arg4  4i   tan    4
4  4i  4   4 
1

2 2
 4 
 32  tan 1  1
4 2 

4
Every complex number can be written in terms of its modulus and
argument
z  x  iy
 r cos  ir sin 
 r cos  i sin  
The mod-arg form of z is;
z  r cos  i sin  

43. e.g . Find the modulus and argument of 4  4i
arg4  4i   tan    4
4  4i  4   4 
1

2 2
 4 
 32  tan 1  1
4 2 

4
Every complex number can be written in terms of its modulus and
argument
z  x  iy
 r cos  ir sin 
 r cos  i sin  
The mod-arg form of z is;
z  r cos  i sin  
z  rcis

44. e.g . Find the modulus and argument of 4  4i
arg4  4i   tan    4
4  4i  4   4 
1

2 2
 4 
 32  tan 1  1
4 2 

4
Every complex number can be written in terms of its modulus and
argument
z  x  iy
 r cos  ir sin 
 r cos  i sin  
The mod-arg form of z is;
z  r cos  i sin  
z  rcis
where; r  z
  arg z

45. e.g. i  4  4i

46. 
e.g. i  4  4i  4 2cis  
 
 4

47. 
e.g. i  4  4i  4 2cis  
 
 4
ii  3  i

48. 
e.g. i  4  4i  4 2cis  
 
 4
ii  3  i
z  3 2
 12
 4
2

49. 
e.g. i  4  4i  4 2cis  
 
 4
ii  3  i
z  3 2
1
2
arg z  tan 1
1
3
 4
2

50. 
e.g. i  4  4i  4 2cis  
 
 4
ii  3  i
z  3 2
1
2
arg z  tan 1
1
 3
 4 
6
2

51. 
e.g. i  4  4i  4 2cis  
 
 4
ii  3  i
z  3 2
1
2
arg z  tan 1
1
 3
 4 
6
2

 3  i  2cis
6

52. 
e.g. i  4  4i  4 2cis  
 
 4
ii  3  i
z  3 2
1
2
arg z  tan 1
1
 3
 4 
6
2

 3  i  2cis
6
Exercise 4B; evens