Embed presentation
Download as PDF, PPTX












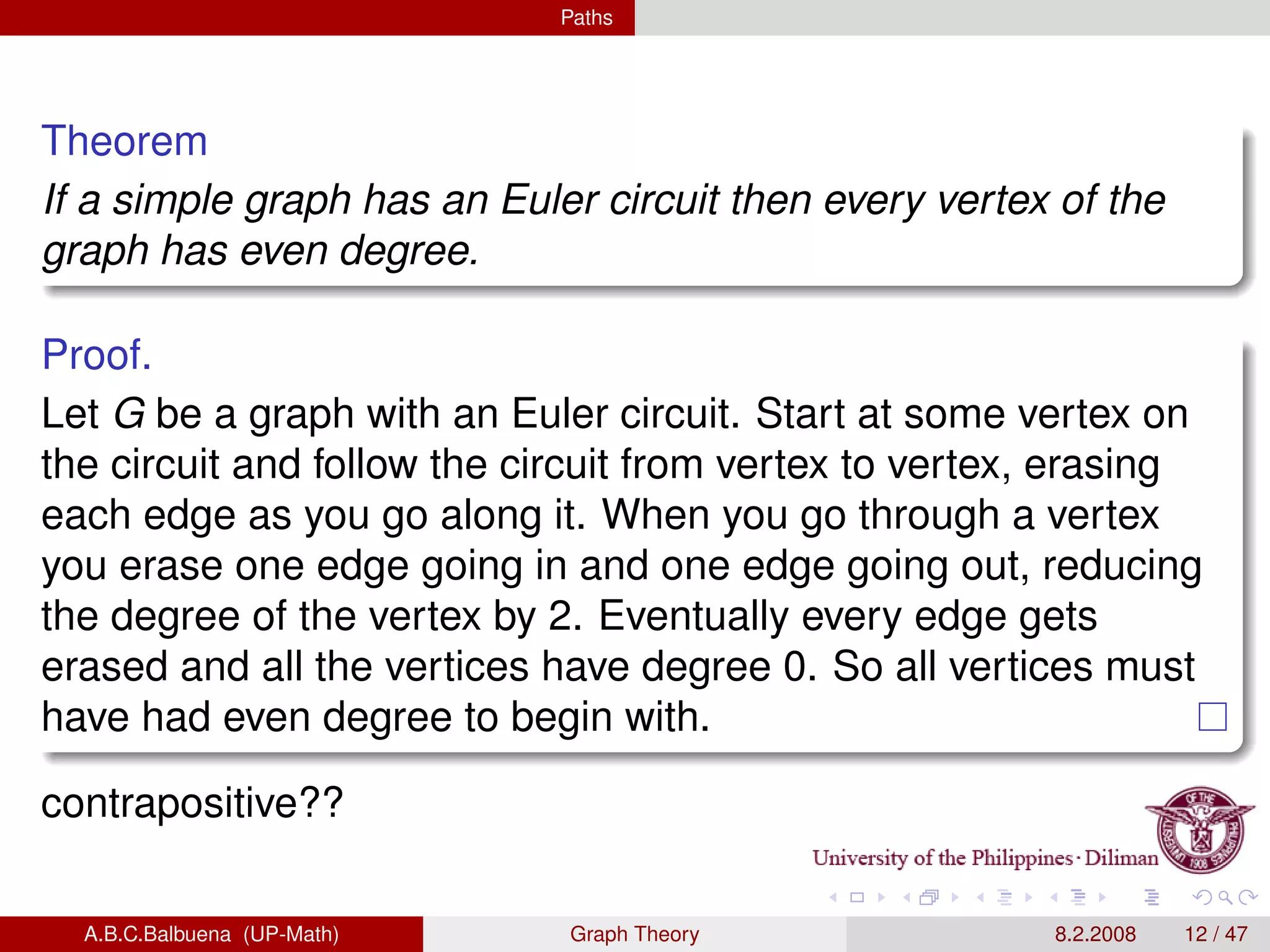




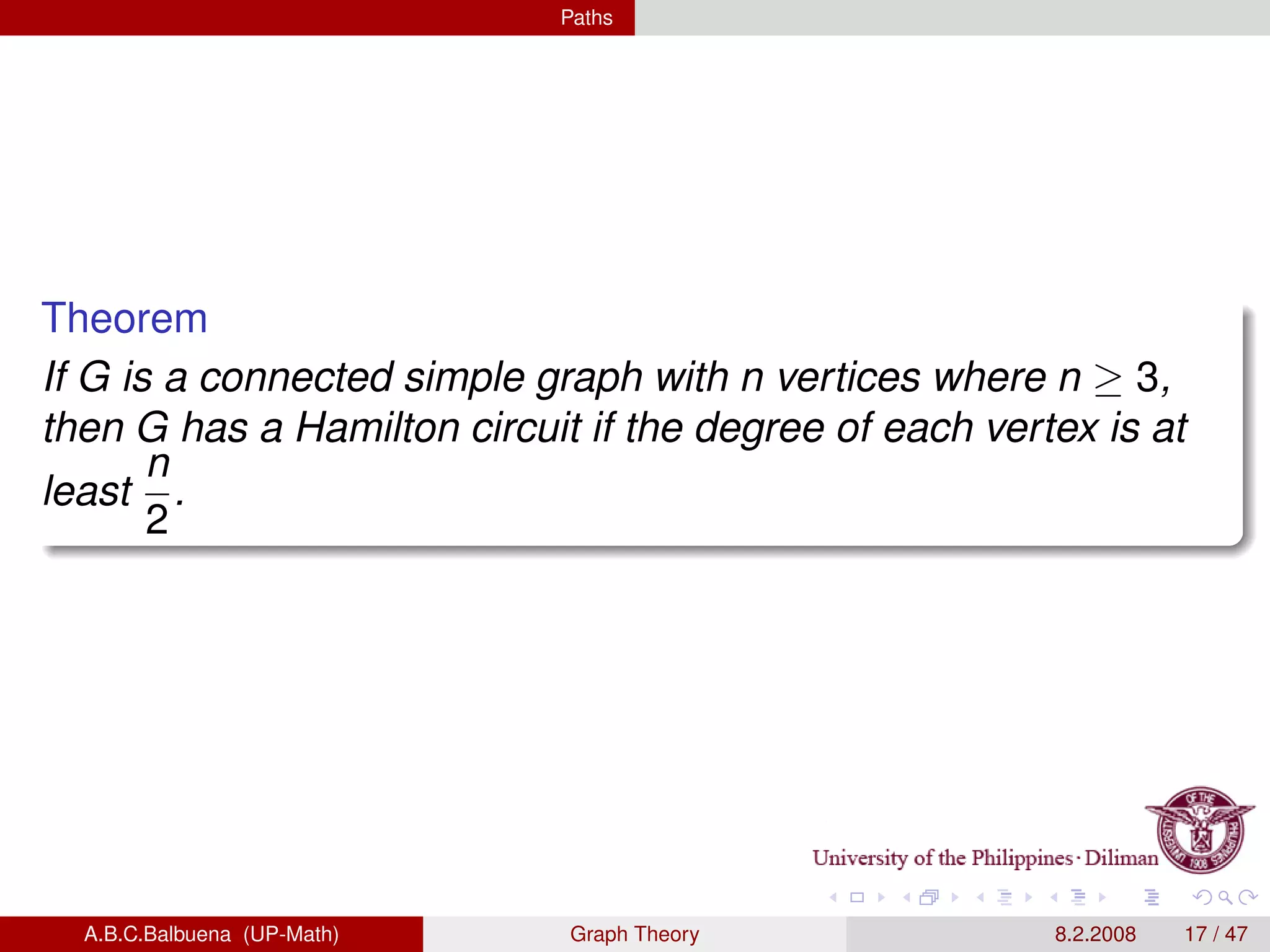

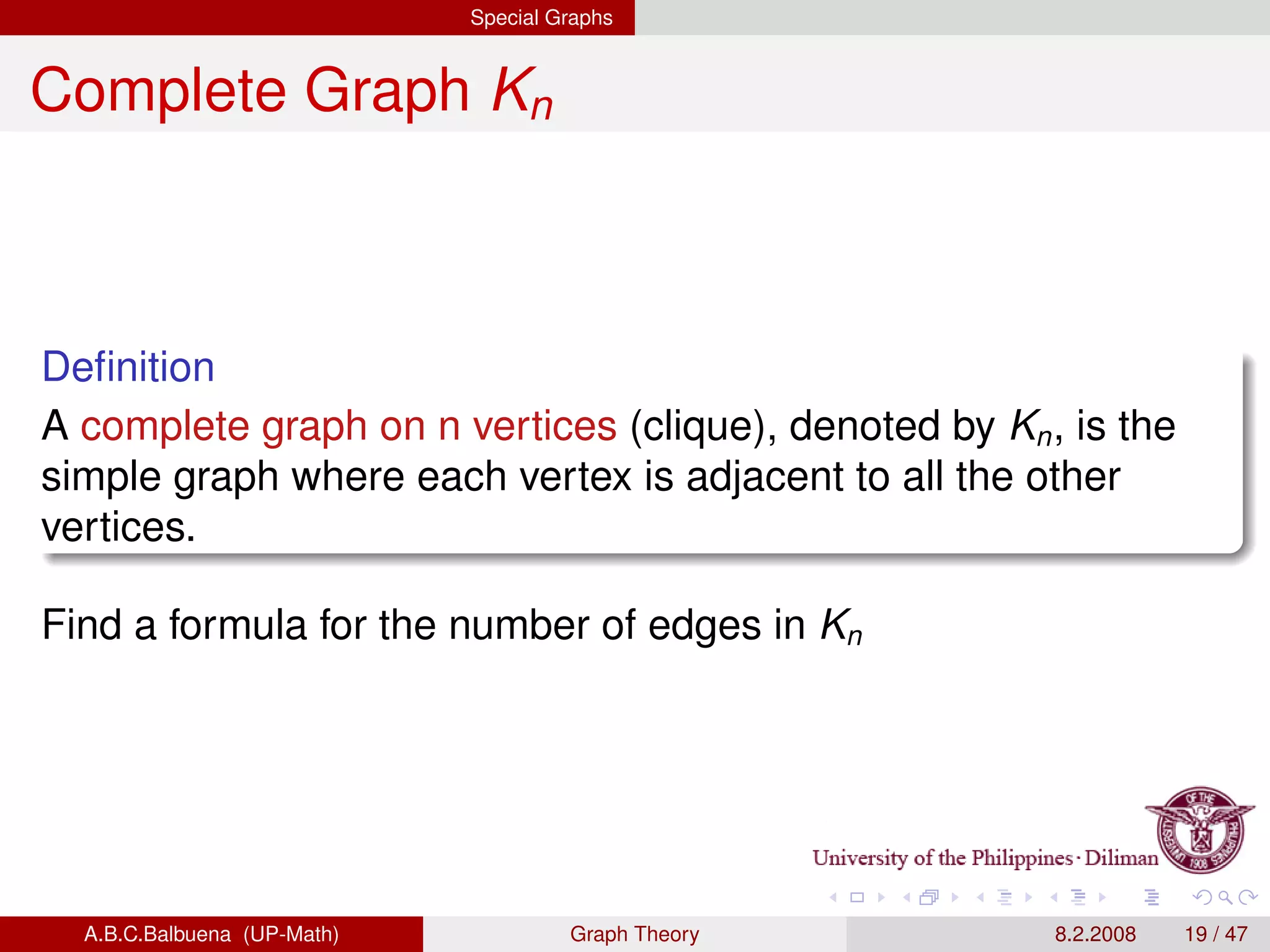
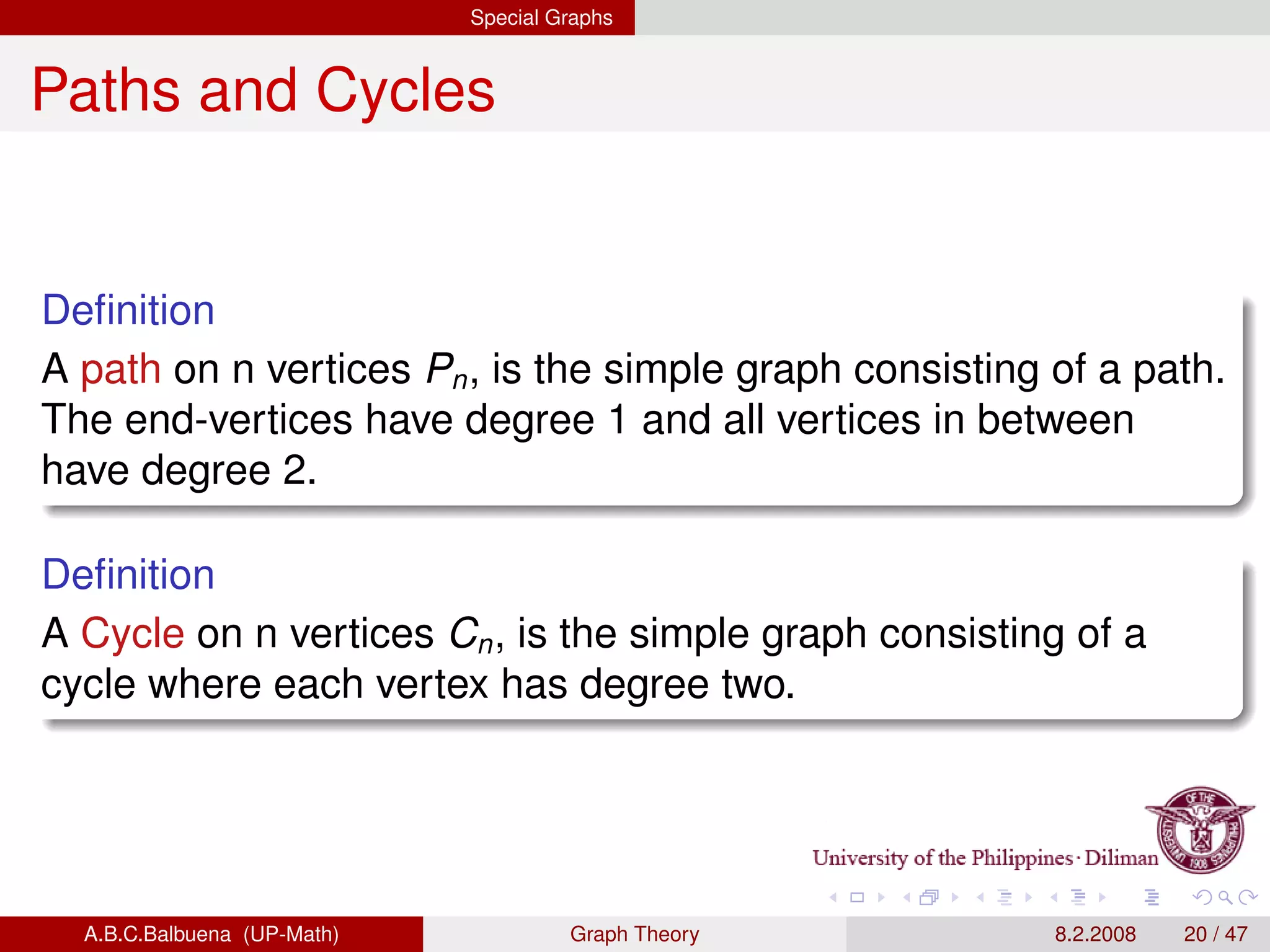
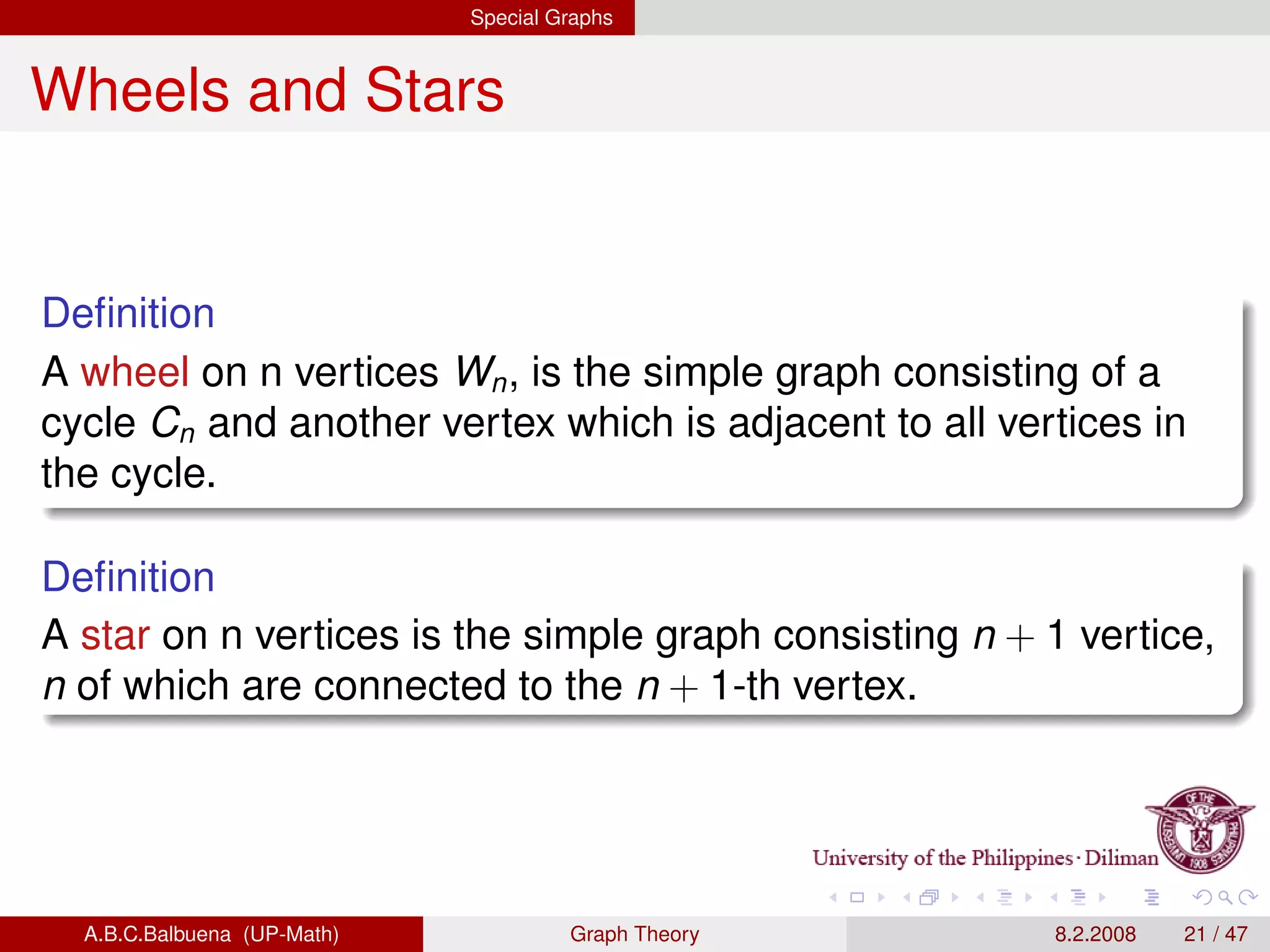

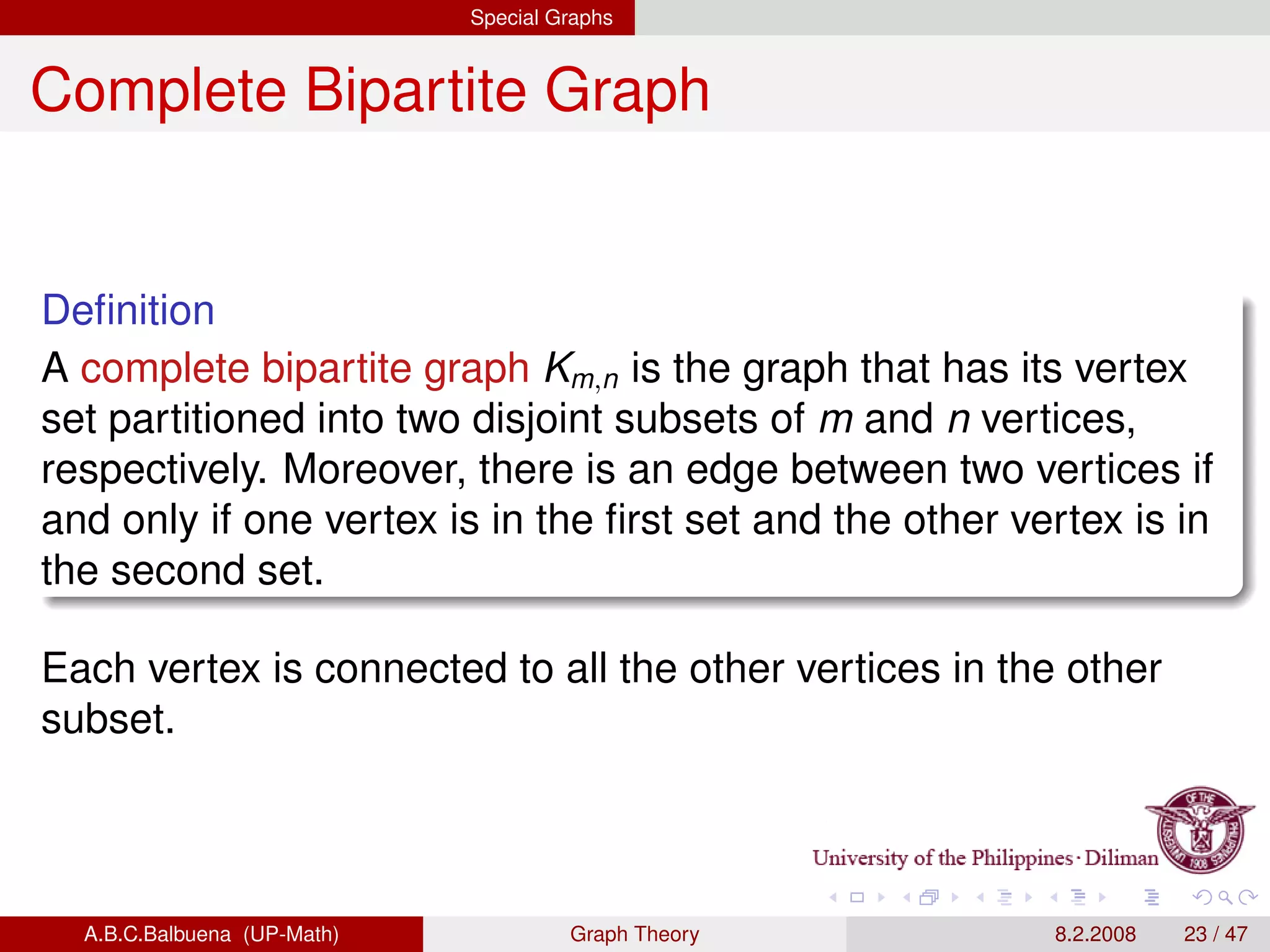

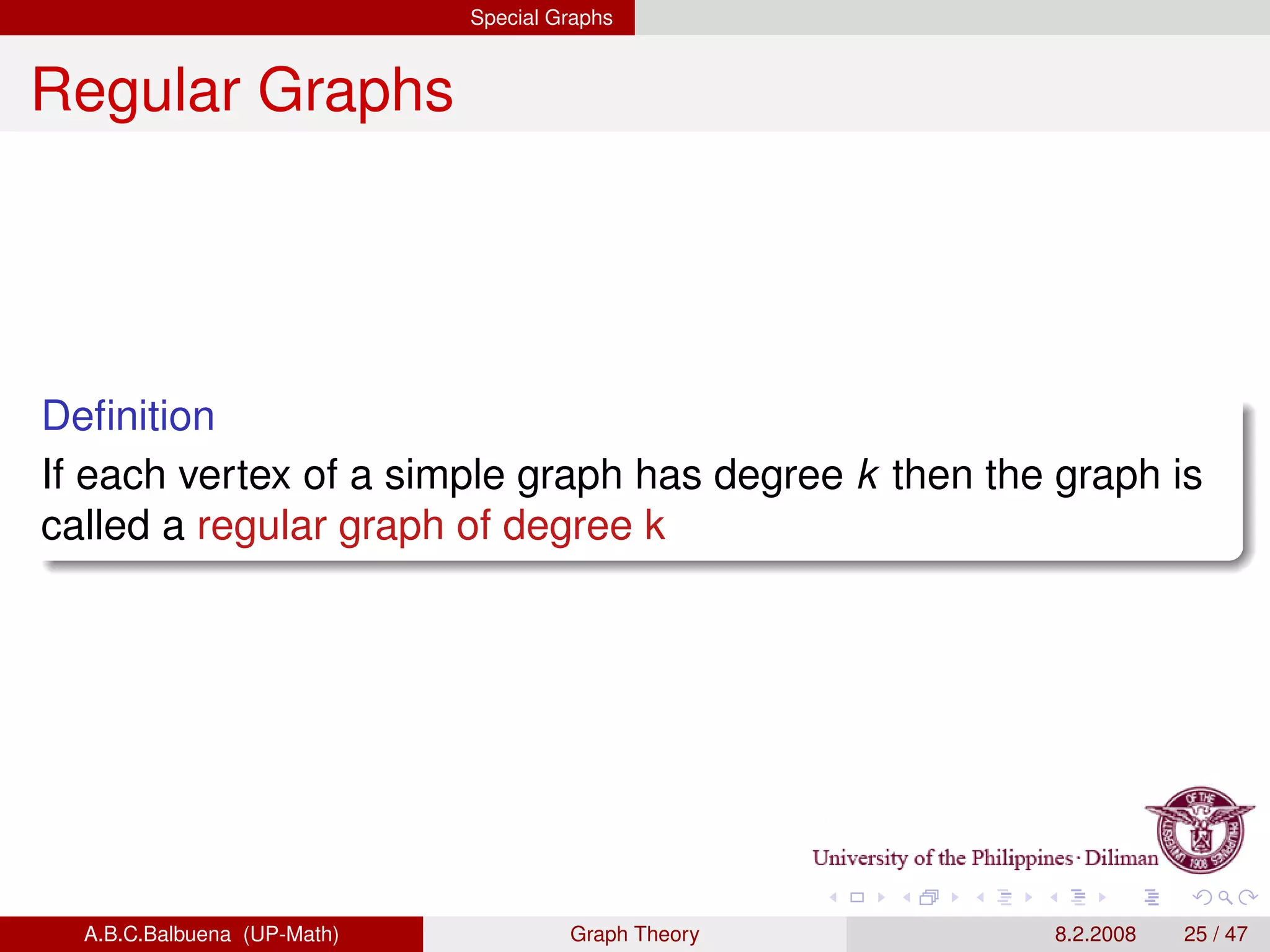





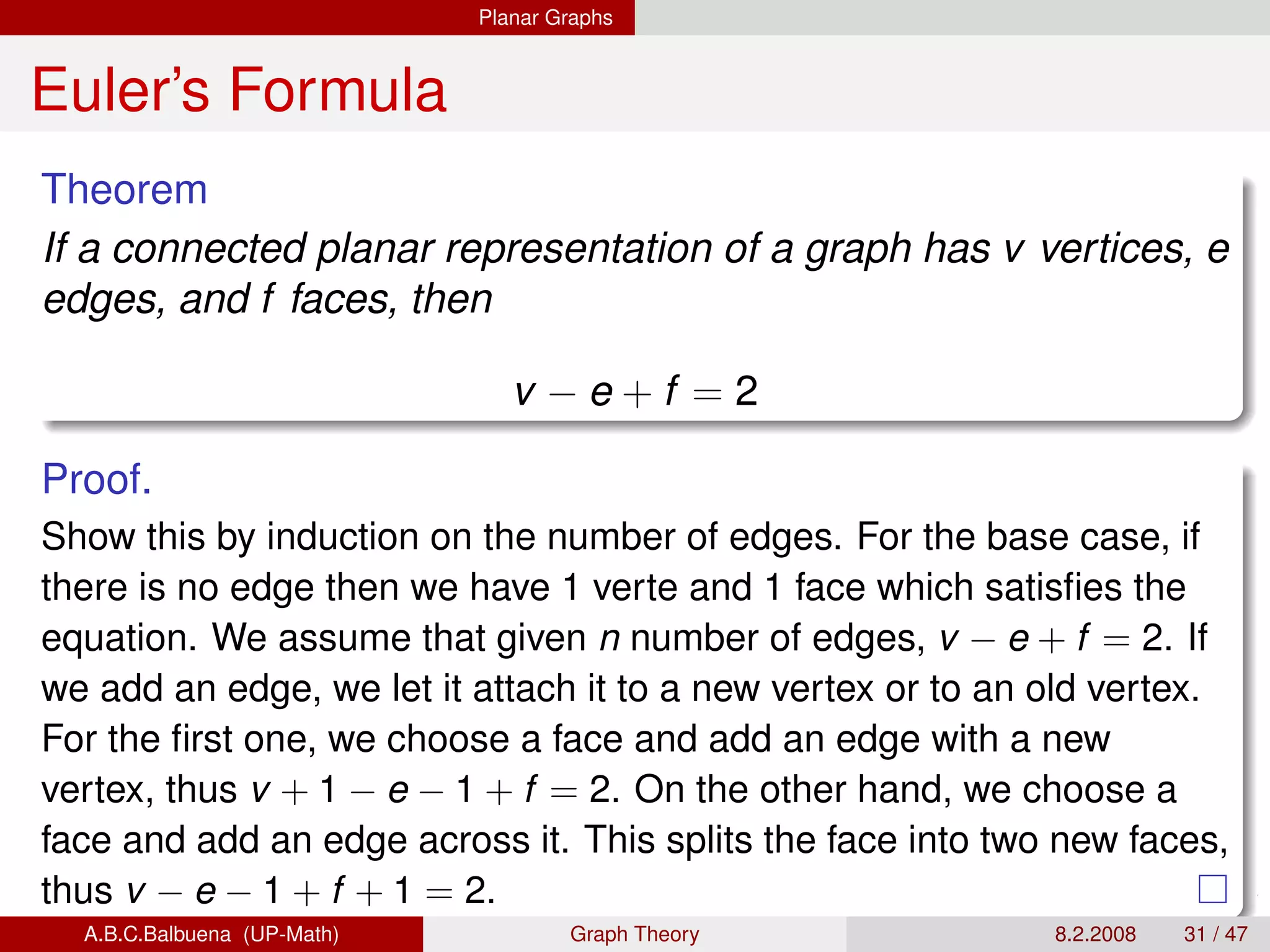









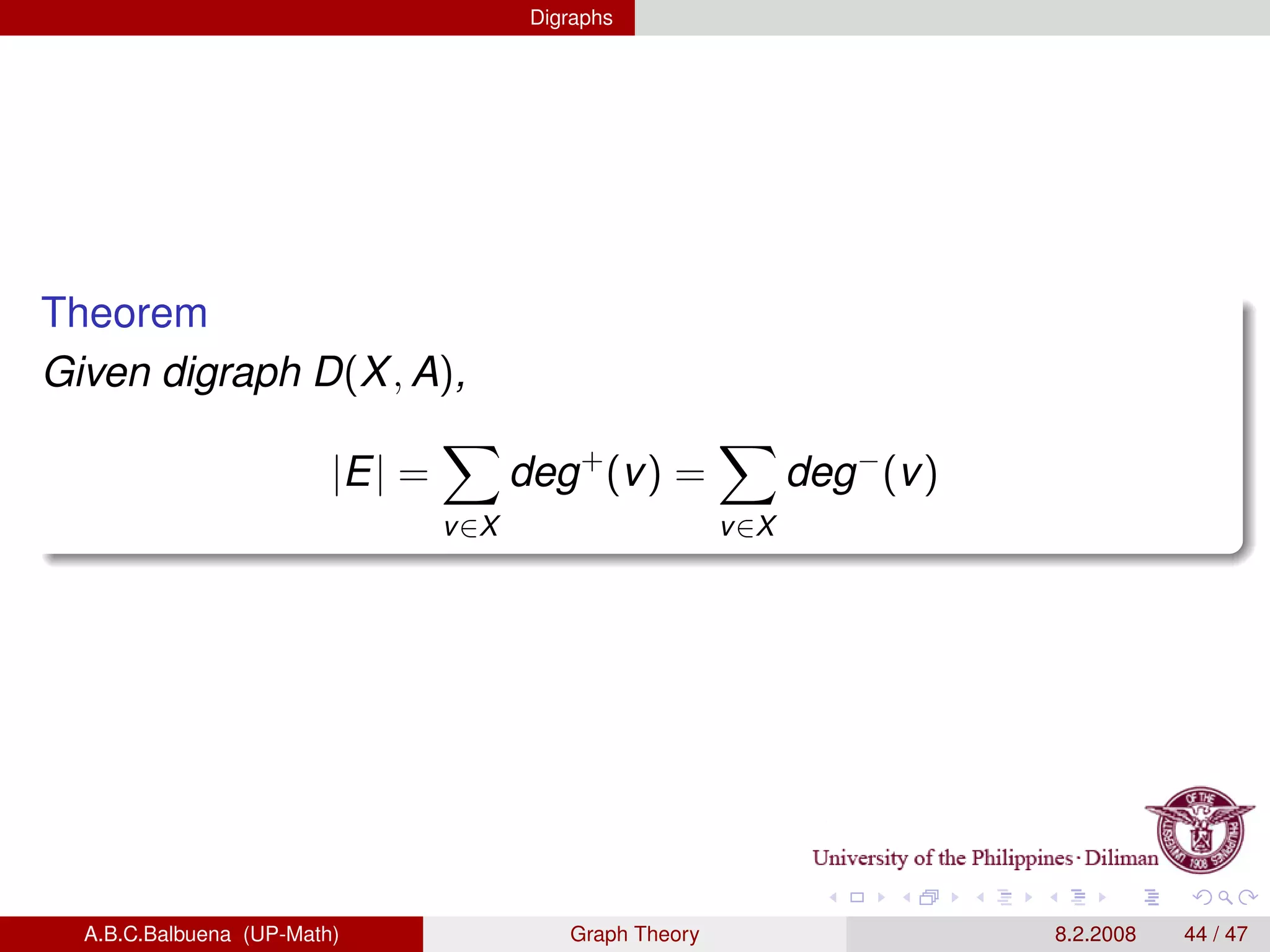


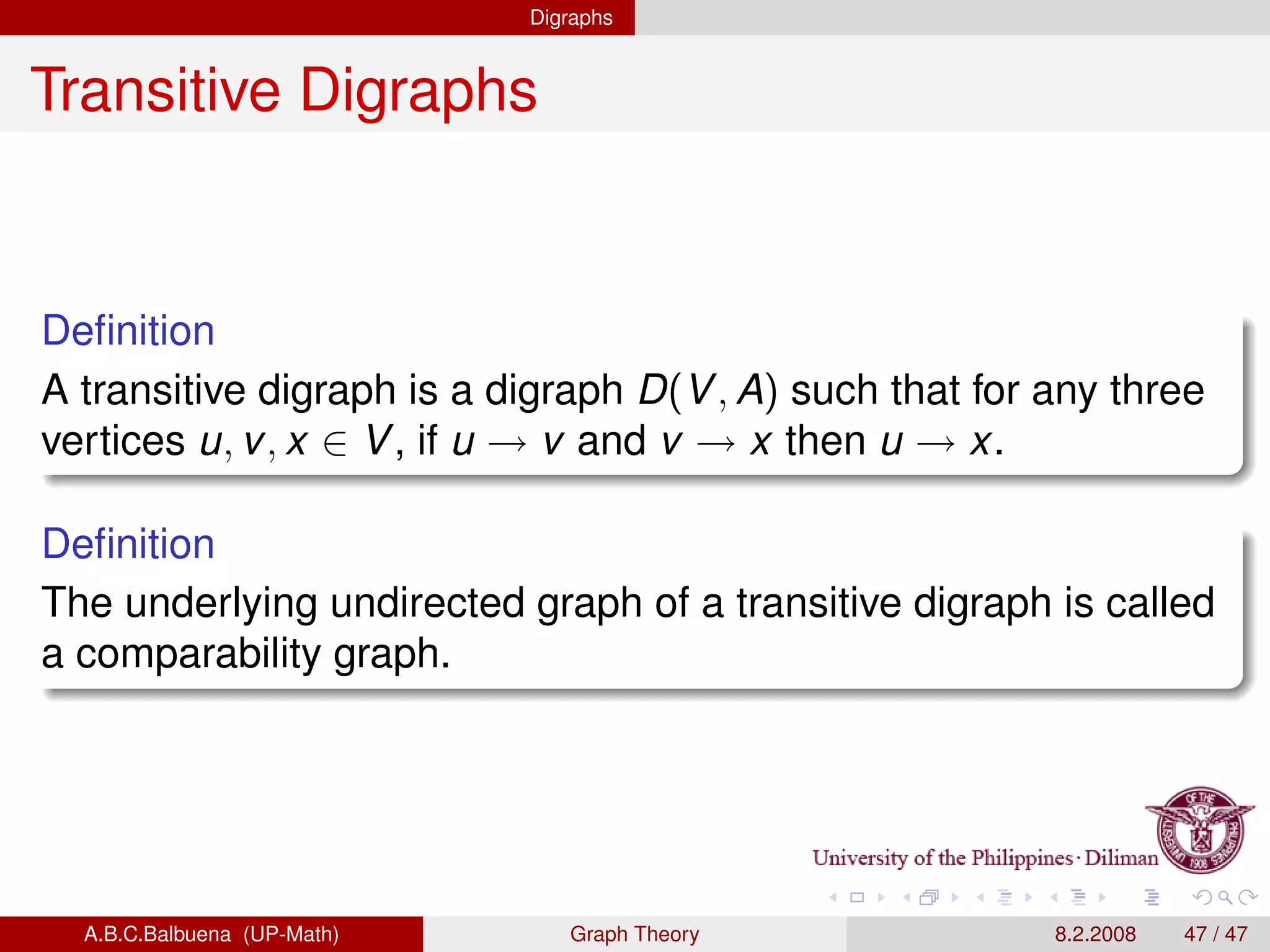

This document provides definitions and theorems related to graph theory. It begins with definitions of simple graphs, vertices, edges, degree, and the handshaking lemma. It then covers definitions and properties of paths, cycles, adjacency matrices, connectedness, Euler paths and circuits. The document also discusses Hamilton paths, planar graphs, trees, and other special types of graphs like complete graphs and bipartite graphs. It provides examples and proofs of many graph theory concepts and results.
















































