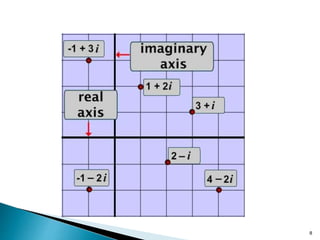
The document explains the progression of number systems starting from natural numbers to integers, rationals, irrationals, and finally complex numbers. It introduces the concept of complex numbers as encompassing real and imaginary parts, illustrated with examples and operations such as addition and multiplication. The document also touches on the conjugate of complex numbers and techniques for simplifying them.

1. Lesson P.6 (pg:60)

2.  In the beginning there were counting
numbers (Natural Numbers)
 And then we needed Integers
1
2

3.  In the beginning there were counting
numbers
 And then we needed integers
1
-1 2
-3

4.  In the beginning there were counting
numbers
 And then we needed integers
 And rationals
1
-1 2
-3
0.41

5.  In the beginning there were counting
numbers
 And then we needed integers
 And rationals
 And irrationals
1
-1 2
-3
0.41
2

6.  In the beginning there were counting
numbers
 And then we needed integers
 And rationals
 And irrationals
 And reals
1
-1 2
-3
0.41
2

0

7. 1
2

8. 8

9. 9

10.  By definition
 Consider powers if i
1  i  i2  1
10
2
i
1
i 3 i 2
i i
i 4 i 2 i
2
i 5 i 4
i i i
1 1 1
1
...
 
   
      
    
It's any
number
you can
imagine

11. i 
i






2
3
4
5
6
7
i
i
i
i
i
i

12.  
i 
i
   





3
4
5
6
7
2
2 1 1
i
i
i
i
i
i

13.  
i 
i
   
1 1
i
i   1
 i  
i
   



3
4
5
6
7
2
2
1 1 1
i
i
i
i

14. i  i  i  i 
i
i i i i
    
i  i  i  i  
i
1
1
1 5 9 13
2 6 10 14
3 7 11 15
4 8 12 16
i i i i
   

15. 15

16.  Now we can handle quantities that
occasionally show up in mathematical
solutions
 What about
16
a  1 a  i a
49 18

17.  Combine real numbers with imaginary
numbers
◦ a + bi
 Examples
17
Real part
Imaginary
part
3 4i
3
 6
 i
2
4.5  i  2 6

18. We have always used them. 6 is not just 6 it is
6 + 0i. Complex numbers incorporate all
numbers.
1
2i 3 + 4i
-1 2
-3
0.41
2

0

19. Note:
 A number such as 3i is a purely imaginary
number
 A number such as 6 is a purely real number
 a + ib is the general form of a complex
number
 6 + 3i is a complex number
 -2 + 7i is also a complex number

20.  If x + iy = 6 – 4i
 then x = 6 and y = -4
 The ‘real part’ of 6 – 4i is 6
 The ‘imaginary part’ of 6 – 4i is -4
20

21.  3i = 0 + 3i
 -7= -7 + 0i
 0= 0 + 0i

22.  Write these complex numbers in standard
form a + bi
 1. 2.
 3. 4.
22
9  75 16 7
5 144  100

23.  Complex numbers can be combined with
◦ Addition
◦ Subtraction
◦ Multiplication
◦ Division
3i8 2i
912i715i
23
24i43i
i
 i
3
5 2

24.  Example 1:
24
24i43i

25.  Example 2:
25
3i8 2i

26.  Example 3:
 (Use FOIL method)
26
912i715i

27.  We need to know Conjugate of a+bi= a-bi
 (Conjugate of a complex number is obtained
by changing the sign of the imaginary part)
For example:
27

28. 28

29.  To solve
 Multiply and divide by
its conjugate
29

30. Qs. Simplify
2
3i  7
The trick is to make the denominator real:

31. 6. Simplify
2
37i 
The trick is to make the denominator real:
i i
2 3 7 2(3 7)
3 7 3 7 58
 
 
i i
  
i
(3 
7)
29
i
7 3
29





32.  Example 4:
i
i 
 Division technique
◦ Multiply numerator and denominator by the
conjugate of the denominator
32
3
52
i i
i i
i i
3 5 2
5 2 5 2
15 6
2
25 4
i
2
6 15 i
6 15
29 29 29
i

3
5 2
 
 



 
   
i
 i

33. 1. Simplify
4

34. Evaluate : 34ii

36. 3. Simplify
34ii

37. 6. Simplify
2
37i 

38. 7. 6 13 0 2
6  36 
52
2
6  
16
2
6  16 
1
2
x
x



x i complexsolutions Conjugates
3 2 ( )
x
Solve x x
 
  

39.  Use the correct principles to simplify the
following:
39
3  121
4  81 4  81
 2
3 144

40.  Lesson P.6
 Page - 65
 Exercises 1 – 32, 37, 38,
 41, 42, 55-62
40