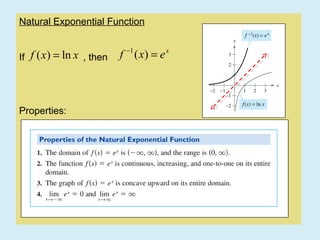
This document discusses derivatives of exponential functions. It covers: 1) The natural exponential function and its inverse, the natural logarithm function. 2) Solving exponential and natural logarithm equations by rewriting one in terms of the other with base e. 3) The derivatives of exponential functions with bases including b, e, and e to the power of u, and examples of differentiating specific exponential functions.

1. Derivatives of
Exponential Functions

2. Natural Exponential Function
If f ( x ) = ln x , then
Properties:
f −1 ( x) = e x

3. Solving Exponential – Natural Log Functions:
Rewrite one as the other with base e
Example: Solve
ln( x + 1) = 6
2
2 ln ( x +1) = 6
ln ( x +1) = 3
e = x+1
3
x= e −1
3

4. d  x x
b  = b ln b
dx
d  u u
du
4.
b  = b ln b ×
dx
dx
3.
Example: Find the derivative
f ( x) = e
f '( x) = e
−
−
1
x2
1
x2
2
× 3
x

5. Differentiate the
following
functions:
1.
2.
3.
4.
d  x x
2  = 2 ln 2
dx
d  −2 x  −2 x
e  = e ×(−2) = −2e−2 x

dx
d  x3  x3
2
2 x3
e  = e ×3x = 3x e
dx
d  cos x  cos x
e  = e ×(−sin x) = − ( sin x ) ecos x

dx

6. Use logarithmic
differentiation to find
sin x 
d 2
( x +1) 

dx 
Solution:
y = ( x +1)
2
sin x
ln y = ln ( x +1)
2
sin x
ln y = ( sin x ) ln ( x 2 +1)
1 dy
1
= ( cos x ) ln ( x 2 +1) + ( sin x ) 2 2x
y dx
x +1
2x ( sin x ) 
dy 
2
= ( cos x ) ln ( x +1) +
 ×y
2
dx 
x +1 
sin x
2x ( sin x )  2
dy 
2
= ( cos x ) ln ( x +1) +
 ×( x +1)
2
dx 
x +1 

7. Let’s Practice!!!
Differentiate each of the following:
1.
ex
y=
ln x
2.
y = ( x + 3)
3.
y = ln ( cos−1 x )
4.
y = cot −1 x
2
ln x