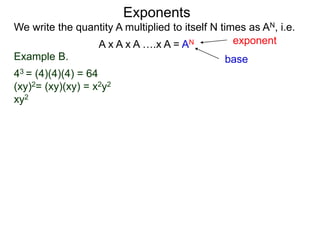
The document discusses exponents and the rules for working with them. Exponents describe the number of times a base is multiplied by itself. The main rules covered are: - The multiply-add rule: When the same base has two exponents, you add the exponents and multiply the results, written as ANAK = AN+K - The divide-subtract rule: When dividing exponents with the same base, you subtract the exponents and divide the results, written as AN/AK = AN-K Examples are provided to demonstrate calculating exponents using these rules.

1. Exponents

2. In the notation
23
Exponents

3. In the notation
23this is the base
Exponents

4. In the notation
= 2 * 2 * 223this is the base
this is the exponent,
or the power, which is
the number of repetitions.
Exponents

5. In the notation
= 2 * 2 * 223this is the base
this is the exponent,
or the power, which is
the number of repetitions.
= 8
Exponents

6. In the notation
= 2 * 2 * 223this is the base
this is the exponent,
or the power, which is
the number of repetitions.
We say that “2 to the power 3 is 8” or
that “2 to the 3rd power is 8.”
= 8
Exponents

7. In the notation
= 2 * 2 * 223this is the base
this is the exponent,
or the power, which is
the number of repetitions.
The Base-1 Rule: 1 any power = 1 * 1 * ..*1 = 1.
We say that “2 to the power 3 is 8” or
that “2 to the 3rd power is 8.”
= 8
Exponents

8. In the notation
= 2 * 2 * 223this is the base
this is the exponent,
or the power, which is
the number of repetitions.
The Base-1 Rule: 1 any power = 1 * 1 * ..*1 = 1.
The Blank-1Power : The expression x (with blank power) is x1,
so 2 = 21, 7 = 71, etc.., i.e. we have one copy of x.
We say that “2 to the power 3 is 8” or
that “2 to the 3rd power is 8.”
= 8
Exponents

9. In the notation
= 2 * 2 * 223this is the base
this is the exponent,
or the power, which is
the number of repetitions.
Example A. Calculate the following.
The Base-1 Rule: 1 any power = 1 * 1 * ..*1 = 1.
The Blank-1Power : The expression x (with blank power) is x1,
so 2 = 21, 7 = 71, etc.., i.e. we have one copy of x.
We say that “2 to the power 3 is 8” or
that “2 to the 3rd power is 8.”
= 8
a. 3(4) b. 34 c. 43
Exponents

10. In the notation
= 2 * 2 * 223this is the base
this is the exponent,
or the power, which is
the number of repetitions.
Example A. Calculate the following.
The Base-1 Rule: 1 any power = 1 * 1 * ..*1 = 1.
The Blank-1Power : The expression x (with blank power) is x1,
so 2 = 21, 7 = 71, etc.., i.e. we have one copy of x.
We say that “2 to the power 3 is 8” or
that “2 to the 3rd power is 8.”
= 8
= 12
a. 3(4) b. 34 c. 43
Exponents

11. In the notation
= 2 * 2 * 223this is the base
this is the exponent,
or the power, which is
the number of repetitions.
Example A. Calculate the following.
The Base-1 Rule: 1 any power = 1 * 1 * ..*1 = 1.
The Blank-1Power : The expression x (with blank power) is x1,
so 2 = 21, 7 = 71, etc.., i.e. we have one copy of x.
We say that “2 to the power 3 is 8” or
that “2 to the 3rd power is 8.”
= 8
= 12 = 3*3*3*3
a. 3(4) b. 34 c. 43
Exponents

12. In the notation
= 2 * 2 * 223this is the base
this is the exponent,
or the power, which is
the number of repetitions.
Example A. Calculate the following.
The Base-1 Rule: 1 any power = 1 * 1 * ..*1 = 1.
The Blank-1Power : The expression x (with blank power) is x1,
so 2 = 21, 7 = 71, etc.., i.e. we have one copy of x.
We say that “2 to the power 3 is 8” or
that “2 to the 3rd power is 8.”
= 8
= 12 = 3*3*3*3
= 9 9*
a. 3(4) b. 34 c. 43
Exponents

13. In the notation
= 2 * 2 * 223this is the base
this is the exponent,
or the power, which is
the number of repetitions.
Example A. Calculate the following.
The Base-1 Rule: 1 any power = 1 * 1 * ..*1 = 1.
The Blank-1Power : The expression x (with blank power) is x1,
so 2 = 21, 7 = 71, etc.., i.e. we have one copy of x.
We say that “2 to the power 3 is 8” or
that “2 to the 3rd power is 8.”
= 8
= 12 = 3*3*3*3
= 9 9*
= 81
a. 3(4) b. 34 c. 43
Exponents

14. In the notation
= 2 * 2 * 223this is the base
this is the exponent,
or the power, which is
the number of repetitions.
Example A. Calculate the following.
The Base-1 Rule: 1 any power = 1 * 1 * ..*1 = 1.
The Blank-1Power : The expression x (with blank power) is x1,
so 2 = 21, 7 = 71, etc.., i.e. we have one copy of x.
We say that “2 to the power 3 is 8” or
that “2 to the 3rd power is 8.”
= 8
= 12 = 3*3*3*3
= 9 9*
= 81
= 4 * 4 * 4
a. 3(4) b. 34 c. 43
Exponents

15. In the notation
= 2 * 2 * 223this is the base
this is the exponent,
or the power, which is
the number of repetitions.
Example A. Calculate the following.
The Base-1 Rule: 1 any power = 1 * 1 * ..*1 = 1.
The Blank-1Power : The expression x (with blank power) is x1,
so 2 = 21, 7 = 71, etc.., i.e. we have one copy of x.
We say that “2 to the power 3 is 8” or
that “2 to the 3rd power is 8.”
= 8
= 12 = 3*3*3*3
= 9 9*
= 81
= 4 * 4 * 4
a. 3(4) b. 34 c. 43
= 16 * 4
= 64
Exponents

16. base
exponent
Exponents
We write the quantity A multiplied to itself N times as AN, i.e.
A x A x A ….x A = AN

17. Example B.
43
base
exponent
Exponents
We write the quantity A multiplied to itself N times as AN, i.e.
A x A x A ….x A = AN

18. Example B.
43 = (4)(4)(4) = 64
base
exponent
Exponents
We write the quantity A multiplied to itself N times as AN, i.e.
A x A x A ….x A = AN

19. Example B.
43 = (4)(4)(4) = 64
(xy)2
base
exponent
Exponents
We write the quantity A multiplied to itself N times as AN, i.e.
A x A x A ….x A = AN

20. Example B.
43 = (4)(4)(4) = 64
(xy)2= (xy)(xy)
base
exponent
Exponents
We write the quantity A multiplied to itself N times as AN, i.e.
A x A x A ….x A = AN

21. Example B.
43 = (4)(4)(4) = 64
(xy)2= (xy)(xy) = x2y2
base
exponent
Exponents
We write the quantity A multiplied to itself N times as AN, i.e.
A x A x A ….x A = AN

22. Example B.
43 = (4)(4)(4) = 64
(xy)2= (xy)(xy) = x2y2
xy2
base
exponent
Exponents
We write the quantity A multiplied to itself N times as AN, i.e.
A x A x A ….x A = AN

23. Example B.
43 = (4)(4)(4) = 64
(xy)2= (xy)(xy) = x2y2
xy2 = (x)(yy)
base
exponent
Exponents
We write the quantity A multiplied to itself N times as AN, i.e.
A x A x A ….x A = AN

24. Example B.
43 = (4)(4)(4) = 64
(xy)2= (xy)(xy) = x2y2
xy2 = (x)(yy)
–x2 = –(xx)
base
exponent
Exponents
We write the quantity A multiplied to itself N times as AN, i.e.
A x A x A ….x A = AN

25. Example B.
43 = (4)(4)(4) = 64
(xy)2= (xy)(xy) = x2y2
xy2 = (x)(yy)
–x2 = –(xx)
base
exponent
Exponents
We write the quantity A multiplied to itself N times as AN, i.e.
A x A x A ….x A = AN

26. Example B.
43 = (4)(4)(4) = 64
(xy)2= (xy)(xy) = x2y2
xy2 = (x)(yy)
–x2 = –(xx)
base
exponent
Exponents
Rules of Exponents
We write the quantity A multiplied to itself N times as AN, i.e.
A x A x A ….x A = AN

27. Example B.
43 = (4)(4)(4) = 64
(xy)2= (xy)(xy) = x2y2
xy2 = (x)(yy)
–x2 = –(xx)
base
exponent
Exponents
Multiply-Add Rule: ANAK =AN+K
Rules of Exponents
We write the quantity A multiplied to itself N times as AN, i.e.
A x A x A ….x A = AN

28. Example B.
43 = (4)(4)(4) = 64
(xy)2= (xy)(xy) = x2y2
xy2 = (x)(yy)
–x2 = –(xx)
base
exponent
Exponents
Multiply-Add Rule: ANAK =AN+K
Example C .
a. 5354
Rules of Exponents
We write the quantity A multiplied to itself N times as AN, i.e.
A x A x A ….x A = AN

29. Example B.
43 = (4)(4)(4) = 64
(xy)2= (xy)(xy) = x2y2
xy2 = (x)(yy)
–x2 = –(xx)
base
exponent
Exponents
Multiply-Add Rule: ANAK =AN+K
Example C .
a. 5354 = (5*5*5)(5*5*5*5)
Rules of Exponents
We write the quantity A multiplied to itself N times as AN, i.e.
A x A x A ….x A = AN

30. Example B.
43 = (4)(4)(4) = 64
(xy)2= (xy)(xy) = x2y2
xy2 = (x)(yy)
–x2 = –(xx)
base
exponent
Exponents
Multiply-Add Rule: ANAK =AN+K
Example C .
a. 5354 = (5*5*5)(5*5*5*5) = 53+4 = 57
b. x5y7x4y6
Rules of Exponents
We write the quantity A multiplied to itself N times as AN, i.e.
A x A x A ….x A = AN

31. Example B.
43 = (4)(4)(4) = 64
(xy)2= (xy)(xy) = x2y2
xy2 = (x)(yy)
–x2 = –(xx)
base
exponent
Exponents
Multiply-Add Rule: ANAK =AN+K
Example C .
a. 5354 = (5*5*5)(5*5*5*5) = 53+4 = 57
b. x5y7x4y6 = x5x4y7y6
Rules of Exponents
We write the quantity A multiplied to itself N times as AN, i.e.
A x A x A ….x A = AN

32. Example B.
43 = (4)(4)(4) = 64
(xy)2= (xy)(xy) = x2y2
xy2 = (x)(yy)
–x2 = –(xx)
base
exponent
Exponents
Multiply-Add Rule: ANAK =AN+K
Example C .
a. 5354 = (5*5*5)(5*5*5*5) = 53+4 = 57
b. x5y7x4y6 = x5x4y7y6 = x9y13
Rules of Exponents
We write the quantity A multiplied to itself N times as AN, i.e.
A x A x A ….x A = AN

33. Example B.
43 = (4)(4)(4) = 64
(xy)2= (xy)(xy) = x2y2
xy2 = (x)(yy)
–x2 = –(xx)
base
exponent
Exponents
Multiply-Add Rule: ANAK =AN+K
Example C .
a. 5354 = (5*5*5)(5*5*5*5) = 53+4 = 57
b. x5y7x4y6 = x5x4y7y6 = x9y13
Rules of Exponents
Divide-Subtract Rule: AN
AK = AN – K
We write the quantity A multiplied to itself N times as AN, i.e.
A x A x A ….x A = AN
Example D .
56
52 =

34. Example B.
43 = (4)(4)(4) = 64
(xy)2= (xy)(xy) = x2y2
xy2 = (x)(yy)
–x2 = –(xx)
base
exponent
Exponents
Multiply-Add Rule: ANAK =AN+K
Example C .
a. 5354 = (5*5*5)(5*5*5*5) = 53+4 = 57
b. x5y7x4y6 = x5x4y7y6 = x9y13
Rules of Exponents
Divide-Subtract Rule: AN
AK = AN – K
We write the quantity A multiplied to itself N times as AN, i.e.
A x A x A ….x A = AN
Example D .
56
52 =
(5)(5)(5)(5)(5)(5)
(5)(5)

35. Example B.
43 = (4)(4)(4) = 64
(xy)2= (xy)(xy) = x2y2
xy2 = (x)(yy)
–x2 = –(xx)
base
exponent
Exponents
Multiply-Add Rule: ANAK =AN+K
Example C .
a. 5354 = (5*5*5)(5*5*5*5) = 53+4 = 57
b. x5y7x4y6 = x5x4y7y6 = x9y13
Rules of Exponents
Divide-Subtract Rule: AN
AK = AN – K
We write the quantity A multiplied to itself N times as AN, i.e.
A x A x A ….x A = AN
Example D .
56
52 =
(5)(5)(5)(5)(5)(5)
(5)(5)
= 56 – 2

36. Example B.
43 = (4)(4)(4) = 64
(xy)2= (xy)(xy) = x2y2
xy2 = (x)(yy)
–x2 = –(xx)
base
exponent
Exponents
Multiply-Add Rule: ANAK =AN+K
Example C .
a. 5354 = (5*5*5)(5*5*5*5) = 53+4 = 57
b. x5y7x4y6 = x5x4y7y6 = x9y13
Rules of Exponents
Divide-Subtract Rule: AN
AK = AN – K
We write the quantity A multiplied to itself N times as AN, i.e.
A x A x A ….x A = AN
Example D .
56
52 =
(5)(5)(5)(5)(5)(5)
(5)(5)
= 56 – 2 = 54

37. Power-Multiply Rule: (AN)K = ANK
Example E. (34)5 =
Exponents

38. Power-Multiply Rule: (AN)K = ANK
Example E. (34)5 = (34)(34)(34)(34)(34)
Exponents

39. Power-Multiply Rule: (AN)K = ANK
Example E. (34)5 = (34)(34)(34)(34)(34)
= 34+4+4+4+4
= 34*5 = 320
Exponents

40. Power-Multiply Rule: (AN)K = ANK
Example E. (34)5 = (34)(34)(34)(34)(34)
= 34+4+4+4+4
= 34*5 = 320
Exponents
Power-Distribute Rule: (ANBM)K = ANK BMK
Example F. (34 23)5 =

41. Power-Multiply Rule: (AN)K = ANK
Example E. (34)5 = (34)(34)(34)(34)(34)
= 34+4+4+4+4
= 34*5 = 320
Exponents
Power-Distribute Rule: (ANBM)K = ANK BMK
Example F. (34 23)5 = (34 23)(34 23)(34 23)(34 23)(34 23)

42. Power-Multiply Rule: (AN)K = ANK
Example E. (34)5 = (34)(34)(34)(34)(34)
= 34+4+4+4+4
= 34*5 = 320
Exponents
Power-Distribute Rule: (ANBM)K = ANK BMK
Example F. (34 23)5 = (34 23)(34 23)(34 23)(34 23)(34 23)
= 34+4+4+4+4 2 3+3+3+3+3

43. Power-Multiply Rule: (AN)K = ANK
Example E. (34)5 = (34)(34)(34)(34)(34)
= 34+4+4+4+4
= 34*5 = 320
Exponents
Power-Distribute Rule: (ANBM)K = ANK BMK
Example F. (34 23)5 = (34 23)(34 23)(34 23)(34 23)(34 23)
= 34+4+4+4+4 2 3+3+3+3+3
= 34*5 23*5
= 320 215

44. Power-Multiply Rule: (AN)K = ANK
Example E. (34)5 = (34)(34)(34)(34)(34)
= 34+4+4+4+4
= 34*5 = 320
Exponents
Power-Distribute Rule: (ANBM)K = ANK BMK
Example F. (34 23)5 = (34 23)(34 23)(34 23)(34 23)(34 23)
= 34+4+4+4+4 2 3+3+3+3+3
= 34*5 23*5
= 320 215
!Note: (AN ± BM)K = ANK ± BMK, e.g. (2 + 3)2 = 22 + 32.

45. Power-Multiply Rule: (AN)K = ANK
Example E. (34)5 = (34)(34)(34)(34)(34)
= 34+4+4+4+4
= 34*5 = 320
Exponents
Power-Distribute Rule: (ANBM)K = ANK BMK
Example F. (34 23)5 = (34 23)(34 23)(34 23)(34 23)(34 23)
= 34+4+4+4+4 2 3+3+3+3+3
= 34*5 23*5
= 320 215
Non–Positive–Whole–Number Exponents
!Note: (AN ± BM)K = ANK ± BMK, e.g. (2 + 3)2 = 22 + 32.

46. Power-Multiply Rule: (AN)K = ANK
Example E. (34)5 = (34)(34)(34)(34)(34)
= 34+4+4+4+4
= 34*5 = 320
Exponents
Power-Distribute Rule: (ANBM)K = ANK BMK
Example F. (34 23)5 = (34 23)(34 23)(34 23)(34 23)(34 23)
= 34+4+4+4+4 2 3+3+3+3+3
= 34*5 23*5
= 320 215
Let’s extend exponent notation to other types of exponents
such as A0 or A–1.
Non–Positive–Whole–Number Exponents
!Note: (AN ± BM)K = ANK ± BMK, e.g. (2 + 3)2 = 22 + 32.

47. Power-Multiply Rule: (AN)K = ANK
Example E. (34)5 = (34)(34)(34)(34)(34)
= 34+4+4+4+4
= 34*5 = 320
Exponents
Power-Distribute Rule: (ANBM)K = ANK BMK
Example F. (34 23)5 = (34 23)(34 23)(34 23)(34 23)(34 23)
= 34+4+4+4+4 2 3+3+3+3+3
= 34*5 23*5
= 320 215
Let’s extend exponent notation to other types of exponents
such as A0 or A–1. The positive–whole–number exponent
specifies a tangible number of copies of the base to be
multiplied (e.g. A2 = A x A, 2 copies of A).
Non–Positive–Whole–Number Exponents
!Note: (AN ± BM)K = ANK ± BMK, e.g. (2 + 3)2 = 22 + 32.

48. Power-Multiply Rule: (AN)K = ANK
Example E. (34)5 = (34)(34)(34)(34)(34)
= 34+4+4+4+4
= 34*5 = 320
Exponents
Power-Distribute Rule: (ANBM)K = ANK BMK
Example F. (34 23)5 = (34 23)(34 23)(34 23)(34 23)(34 23)
= 34+4+4+4+4 2 3+3+3+3+3
= 34*5 23*5
= 320 215
Let’s extend exponent notation to other types of exponents
such as A0 or A–1. The positive–whole–number exponent
specifies a tangible number of copies of the base to be
multiplied (e.g. A2 = A x A, 2 copies of A). But A0 does not
mean there is “0” copy of A, or that A–1 is “–1” copy of A.
Non–Positive–Whole–Number Exponents
!Note: (AN ± BM)K = ANK ± BMK, e.g. (2 + 3)2 = 22 + 32.

49. Exponents
We extract the meaning of A0 or A–1 by contemplating the
consequences of the above operational rules.

50. Exponents
Since = 1
A1
A1
We extract the meaning of A0 or A–1 by contemplating the
consequences of the above operational rules.

51. Exponents
Since = 1 = A1 – 1 = A0, we obtain the 0-power Rule.
A1
A1
We extract the meaning of A0 or A–1 by contemplating the
consequences of the above operational rules.

52. Exponents
Since = 1 = A1 – 1 = A0, we obtain the 0-power Rule.
A1
A1
0-Power Rule: A0 = 1, A = 0
We extract the meaning of A0 or A–1 by contemplating the
consequences of the above operational rules.

53. Exponents
Since = 1 = A1 – 1 = A0, we obtain the 0-power Rule.
A1
A1
0-Power Rule: A0 = 1, A = 0
We extract the meaning of A0 or A–1 by contemplating the
consequences of the above operational rules.
It's a major intellectual leap for one to
accept that this symbolic system requires
that A0 = 1, and to reject the more intuitive
translation of A0 as “0 copy of A”
which leads to the seemingly
obvious but wrong answer A0 = 0.

54. Exponents
Since = 1 = A1 – 1 = A0, we obtain the 0-power Rule.
A1
A1
Since =
1
A
A0
A1
0-Power Rule: A0 = 1, A = 0
We extract the meaning of A0 or A–1 by contemplating the
consequences of the above operational rules.

55. Exponents
Since = 1 = A1 – 1 = A0, we obtain the 0-power Rule.
A1
A1
Since = = A0 – 1 = A–1, we get the negative-power rule.
1
A
A0
A1
0-Power Rule: A0 = 1, A = 0
We extract the meaning of A0 or A–1 by contemplating the
consequences of the above operational rules.

56. Exponents
Since = 1 = A1 – 1 = A0, we obtain the 0-power Rule.
A1
A1
Since = = A0 – 1 = A–1, we get the negative-power rule.
1
A
A0
A1
Negative-Power Rule: A–1 =
1
A
0-Power Rule: A0 = 1, A = 0
, A = 0
We extract the meaning of A0 or A–1 by contemplating the
consequences of the above operational rules.

57. Exponents
Since = 1 = A1 – 1 = A0, we obtain the 0-power Rule.
A1
A1
Since = = A0 – 1 = A–1, we get the negative-power rule.
1
A
A0
A1
Negative-Power Rule: A–1 =
1
A
0-Power Rule: A0 = 1, A = 0
, A = 0
We extract the meaning of A0 or A–1 by contemplating the
consequences of the above operational rules.
and in general that
1
AKA–K =

58. Exponents
Since = 1 = A1 – 1 = A0, we obtain the 0-power Rule.
A1
A1
Since = = A0 – 1 = A–1, we get the negative-power rule.
1
A
A0
A1
Negative-Power Rule: A–1 =
1
A
0-Power Rule: A0 = 1, A = 0
, A = 0
We extract the meaning of A0 or A–1 by contemplating the
consequences of the above operational rules.
and in general that
1
AK
The “negative” of an exponents mean to reciprocate the base.
A–K =

59. Exponents
Since = 1 = A1 – 1 = A0, we obtain the 0-power Rule.
A1
A1
Since = = A0 – 1 = A–1, we get the negative-power rule.
1
A
A0
A1
Negative-Power Rule: A–1 =
1
A
Example J. Simplify
c. ( )–12
5
=
b. 3–2 =
a. 30 =
0-Power Rule: A0 = 1, A = 0
, A = 0
We extract the meaning of A0 or A–1 by contemplating the
consequences of the above operational rules.
and in general that
1
AK
The “negative” of an exponents mean to reciprocate the base.
A–K =

60. Exponents
Since = 1 = A1 – 1 = A0, we obtain the 0-power Rule.
A1
A1
Since = = A0 – 1 = A–1, we get the negative-power rule.
1
A
A0
A1
Negative-Power Rule: A–1 =
1
A
Example J. Simplify
c. ( )–12
5
b. 3–2 =
a. 30 = 1
0-Power Rule: A0 = 1, A = 0
, A = 0
We extract the meaning of A0 or A–1 by contemplating the
consequences of the above operational rules.
and in general that
1
AK
The “negative” of an exponents mean to reciprocate the base.
A–K =
=

61. Exponents
Since = 1 = A1 – 1 = A0, we obtain the 0-power Rule.
A1
A1
Since = = A0 – 1 = A–1, we get the negative-power rule.
1
A
A0
A1
Negative-Power Rule: A–1 =
1
A
Example J. Simplify
1
32
1
9
c. ( )–12
5
=
b. 3–2 = =
a. 30 = 1
0-Power Rule: A0 = 1, A = 0
, A = 0
We extract the meaning of A0 or A–1 by contemplating the
consequences of the above operational rules.
and in general that
1
AK
The “negative” of an exponents mean to reciprocate the base.
A–K =

62. Exponents
Since = 1 = A1 – 1 = A0, we obtain the 0-power Rule.
A1
A1
Since = = A0 – 1 = A–1, we get the negative-power rule.
1
A
A0
A1
Negative-Power Rule: A–1 =
1
A
Example J. Simplify
1
32
1
9
c. ( )–12
5
=
1
2/5
= 1*
5
2
=
5
2
b. 3–2 = =
a. 30 = 1
0-Power Rule: A0 = 1, A = 0
, A = 0
We extract the meaning of A0 or A–1 by contemplating the
consequences of the above operational rules.
and in general that
1
AK
The “negative” of an exponents mean to reciprocate the base.
A–K =

63. Exponents
Since = 1 = A1 – 1 = A0, we obtain the 0-power Rule.
A1
A1
Since = = A0 – 1 = A–1, we get the negative-power rule.
1
A
A0
A1
Negative-Power Rule: A–1 =
1
A
Example J. Simplify
1
32
1
9
c. ( )–12
5
=
1
2/5
= 1*
5
2
=
5
2
b. 3–2 = =
a. 30 = 1
In general ( )–Ka
b = ( )K
b
a
d. ( )–22
5
=
0-Power Rule: A0 = 1, A = 0
, A = 0
We extract the meaning of A0 or A–1 by contemplating the
consequences of the above operational rules.
and in general that
1
AK
The “negative” of an exponents mean to reciprocate the base.
A–K =

64. Exponents
Since = 1 = A1 – 1 = A0, we obtain the 0-power Rule.
A1
A1
Since = = A0 – 1 = A–1, we get the negative-power rule.
1
A
A0
A1
Negative-Power Rule: A–1 =
1
A
Example J. Simplify
1
32
1
9
c. ( )–12
5
=
1
2/5
= 1*
5
2
=
5
2
b. 3–2 = =
a. 30 = 1
In general ( )–Ka
b = ( )K
b
a
d. ( )–22
5
= ( )2 =
25
4
5
2
0-Power Rule: A0 = 1, A = 0
, A = 0
We extract the meaning of A0 or A–1 by contemplating the
consequences of the above operational rules.
and in general that
1
AK
The “negative” of an exponents mean to reciprocate the base.
A–K =

65. e. 3–1 – 40 * 2–2 =
Exponents

66. e. 3–1 – 40 * 2–2 =
1
3
Exponents

67. e. 3–1 – 40 * 2–2 =
1
3
– 1*
Exponents

68. e. 3–1 – 40 * 2–2 =
1
3
– 1*
1
22
Exponents

69. e. 3–1 – 40 * 2–2 =
1
3
– 1*
1
22 = 1
3
– 1
4
= 1
12
Exponents

70. e. 3–1 – 40 * 2–2 =
1
3
– 1*
1
22 = 1
3
– 1
4
= 1
12
Exponents
Although the negative power means to reciprocate,
for problems of consolidating exponents, we do not
reciprocate the negative exponents.

71. e. 3–1 – 40 * 2–2 =
1
3
– 1*
1
22 = 1
3
– 1
4
= 1
12
Exponents
Although the negative power means to reciprocate,
for problems of consolidating exponents, we do not
reciprocate the negative exponents. Instead we add or
subtract them using the multiplication and division rules first.

72. e. 3–1 – 40 * 2–2 =
Exponents
Although the negative power means to reciprocate,
for problems of consolidating exponents, we do not
reciprocate the negative exponents. Instead we add or
subtract them using the multiplication and division rules first.
Example H. Simplify 3–2 x4 y–6 x–8 y 23
1
3
– 1*
1
22 = 1
3
– 1
4
= 1
12

73. e. 3–1 – 40 * 2–2 =
Exponents
Although the negative power means to reciprocate,
for problems of consolidating exponents, we do not
reciprocate the negative exponents. Instead we add or
subtract them using the multiplication and division rules first.
Example H. Simplify 3–2 x4 y–6 x–8 y 23
3–2 x4 y–6 x–8 y23
1
3
– 1*
1
22 = 1
3
– 1
4
= 1
12

74. e. 3–1 – 40 * 2–2 =
Exponents
Although the negative power means to reciprocate,
for problems of consolidating exponents, we do not
reciprocate the negative exponents. Instead we add or
subtract them using the multiplication and division rules first.
Example H. Simplify 3–2 x4 y–6 x–8 y 23
3–2 x4 y–6 x–8 y23
= 3–2 x4 x–8 y–6 y23
1
3
– 1*
1
22 = 1
3
– 1
4
= 1
12

75. e. 3–1 – 40 * 2–2 =
Exponents
Although the negative power means to reciprocate,
for problems of consolidating exponents, we do not
reciprocate the negative exponents. Instead we add or
subtract them using the multiplication and division rules first.
= x4 – 8 y–6+23
Example H. Simplify 3–2 x4 y–6 x–8 y 23
3–2 x4 y–6 x–8 y23
= 3–2 x4 x–8 y–6 y23
1
9
1
3
– 1*
1
22 = 1
3
– 1
4
= 1
12

76. e. 3–1 – 40 * 2–2 =
Exponents
Although the negative power means to reciprocate,
for problems of consolidating exponents, we do not
reciprocate the negative exponents. Instead we add or
subtract them using the multiplication and division rules first.
= x4 – 8 y–6+23
= x–4 y17
Example H. Simplify 3–2 x4 y–6 x–8 y 23
3–2 x4 y–6 x–8 y23
= 3–2 x4 x–8 y–6 y23
1
9
1
9
1
3
– 1*
1
22 = 1
3
– 1
4
= 1
12

77. e. 3–1 – 40 * 2–2 =
Exponents
Although the negative power means to reciprocate,
for problems of consolidating exponents, we do not
reciprocate the negative exponents. Instead we add or
subtract them using the multiplication and division rules first.
= x4 – 8 y–6+23
= x–4 y17
= y17
Example H. Simplify 3–2 x4 y–6 x–8 y 23
3–2 x4 y–6 x–8 y23
= 3–2 x4 x–8 y–6 y23
1
9
1
9
1
9x4
1
3
– 1*
1
22 = 1
3
– 1
4
= 1
12

78. e. 3–1 – 40 * 2–2 =
Exponents
Although the negative power means to reciprocate,
for problems of consolidating exponents, we do not
reciprocate the negative exponents. Instead we add or
subtract them using the multiplication and division rules first.
= x4 – 8 y–6+23
= x–4 y17
= y17
=
Example H. Simplify 3–2 x4 y–6 x–8 y 23
3–2 x4 y–6 x–8 y23
= 3–2 x4 x–8 y–6 y23
1
9
1
9
1
9x4
y17
9x4
1
3
– 1*
1
22 = 1
3
– 1
4
= 1
12

79. Exponents
Example I. Simplify using the rules for exponents.
Leave the answer in positive exponents only.
23x–8
26 x–3

80. Exponents
Example I. Simplify using the rules for exponents.
Leave the answer in positive exponents only.
23x–8
26 x–3
23x–8
26x–3

81. Exponents
Example I. Simplify using the rules for exponents.
Leave the answer in positive exponents only.
23x–8
26 x–3
23x–8
26x–3
= 23 – 6 x–8 – (–3 )

82. Exponents
Example I. Simplify using the rules for exponents.
Leave the answer in positive exponents only.
23x–8
26 x–3
23x–8
26x–3
= 23 – 6 x–8 – (–3 )
= 2–3 x–5

83. Exponents
Example I. Simplify using the rules for exponents.
Leave the answer in positive exponents only.
23x–8
26 x–3
23x–8
26x–3
= 23 – 6 x–8 – (–3 )
= 2–3 x–5
=
23
1
x5
1
* = 8x5
1

84. Exponents
Example I. Simplify using the rules for exponents.
Leave the answer in positive exponents only.
23x–8
26 x–3
23x–8
26x–3
= 23 – 6 x–8 – (–3 )
= 2–3 x–5
=
23
1
x5
1
* = 8x5
1
Example J. Simplify (3x–2y3)–2 x2
3–5x–3(y–1x2)3

85. Exponents
Example I. Simplify using the rules for exponents.
Leave the answer in positive exponents only.
23x–8
26 x–3
23x–8
26x–3
= 23 – 6 x–8 – (–3 )
= 2–3 x–5
=
23
1
x5
1
* = 8x5
1
Example J. Simplify (3x–2y3)–2 x2
3–5x–3(y–1x2)3
(3x–2y3)–2 x2
3–5x–3(y–1x2)3

86. Exponents
Example I. Simplify using the rules for exponents.
Leave the answer in positive exponents only.
23x–8
26 x–3
23x–8
26x–3
= 23 – 6 x–8 – (–3 )
= 2–3 x–5
=
23
1
x5
1
* = 8x5
1
Example J. Simplify (3x–2y3)–2 x2
3–5x–3(y–1x2)3
=
3–2x4y–6x2
3–5x–3y–3 x6
(3x–2y3)–2 x2
3–5x–3(y–1x2)3

87. Exponents
Example I. Simplify using the rules for exponents.
Leave the answer in positive exponents only.
23x–8
26 x–3
23x–8
26x–3
= 23 – 6 x–8 – (–3 )
= 2–3 x–5
=
23
1
x5
1
* = 8x5
1
Example J. Simplify (3x–2y3)–2 x2
3–5x–3(y–1x2)3
=
3–2x4y–6x2
3–5x–3y–3 x6 =
(3x–2y3)–2 x2
3–5x–3(y–1x2)3 3–5x–3x6y–3
3–2x4x2y–6

88. Exponents
Example I. Simplify using the rules for exponents.
Leave the answer in positive exponents only.
23x–8
26 x–3
23x–8
26x–3
= 23 – 6 x–8 – (–3 )
= 2–3 x–5
=
23
1
x5
1
* = 8x5
1
Example J. Simplify (3x–2y3)–2 x2
3–5x–3(y–1x2)3
=
3–2x4y–6x2
3–5x–3y–3 x6 =
=
(3x–2y3)–2 x2
3–5x–3(y–1x2)3 3–5x–3x6y–3
3–2x4x2y–6
3–2x6y–6
3–5x3y–3

89. Exponents
Example I. Simplify using the rules for exponents.
Leave the answer in positive exponents only.
23x–8
26 x–3
23x–8
26x–3
= 23 – 6 x–8 – (–3 )
= 2–3 x–5
=
23
1
x5
1
* = 8x5
1
Example J. Simplify (3x–2y3)–2 x2
3–5x–3(y–1x2)3
=
3–2x4y–6x2
3–5x–3y–3 x6 =
= = 3–2 – (–5) x6 – 3 y–6 – (–3)
(3x–2y3)–2 x2
3–5x–3(y–1x2)3 3–5x–3x6y–3
3–2x4x2y–6
3–2x6y–6
3–5x3y–3

90. Exponents
Example I. Simplify using the rules for exponents.
Leave the answer in positive exponents only.
23x–8
26 x–3
23x–8
26x–3
= 23 – 6 x–8 – (–3 )
= 2–3 x–5
=
23
1
x5
1
* = 8x5
1
Example J. Simplify (3x–2y3)–2 x2
3–5x–3(y–1x2)3
=
3–2x4y–6x2
3–5x–3y–3 x6 =
= = 3–2 – (–5) x6 – 3 y–6 – (–3)
= 33 x3 y–3=
(3x–2y3)–2 x2
3–5x–3(y–1x2)3 3–5x–3x6y–3
3–2x4x2y–6
3–2x6y–6
3–5x3y–3

91. Exponents
Example I. Simplify using the rules for exponents.
Leave the answer in positive exponents only.
23x–8
26 x–3
23x–8
26x–3
= 23 – 6 x–8 – (–3 )
= 2–3 x–5
=
23
1
x5
1
* = 8x5
1
Example J. Simplify (3x–2y3)–2 x2
3–5x–3(y–1x2)3
=
3–2x4y–6x2
3–5x–3y–3 x6 =
= = 3–2 – (–5) x6 – 3 y–6 – (–3)
= 33 x3 y–3=
27 x3
(3x–2y3)–2 x2
3–5x–3(y–1x2)3 3–5x–3x6y–3
3–2x4x2y–6
3–2x6y–6
3–5x3y–3
y3

92. Exponents
Example I. Simplify using the rules for exponents.
Leave the answer in positive exponents only.
23x–8
26 x–3
23x–8
26x–3
= 23 – 6 x–8 – (–3 )
= 2–3 x–5
=
23
1
x5
1
* = 8x5
1
Example J. Simplify (3x–2y3)–2 x2
3–5x–3(y–1x2)3
=
3–2x4y–6x2
3–5x–3y–3 x6 =
= = 3–2 – (–5) x6 – 3 y–6 – (–3)
= 33 x3 y–3=
27 x3
(3x–2y3)–2 x2
3–5x–3(y–1x2)3 3–5x–3x6y–3
3–2x4x2y–6
3–2x6y–6
3–5x3y–3
y3

93. 0-power Rule: A0 = 1 (A=0)
=
1
Ak
1
Ak
A0
Ak
Special Exponents
½ - Power Rule: A½ = A , the square root of A,
because 1 = = A1–1 = A0A1
A1
Negative Power Rule: A–k =
because = A0–k = A–k
(divide–subtract)
(divide–subtract)

94. 0-power Rule: A0 = 1 (A=0)
=
1
Ak
1
Ak
A0
Ak
Special Exponents
½ - Power Rule: A½ = A , the square root of A,
because (A½)2 = A = (A)2,
because 1 = = A1–1 = A0A1
A1
Negative Power Rule: A–k =
because = A0–k = A–k
(divide–subtract)
(divide–subtract)

95. 0-power Rule: A0 = 1 (A=0)
=
1
Ak
1
Ak
A0
Ak
Special Exponents
½ - Power Rule: A½ = A , the square root of A,
because (A½)2 = A = (A)2, so A½ = A
because 1 = = A1–1 = A0A1
A1
Negative Power Rule: A–k =
because = A0–k = A–k
(divide–subtract)
(divide–subtract)

96. 0-power Rule: A0 = 1 (A=0)
=
1
Ak
1
Ak
A0
Ak
Special Exponents
½ - Power Rule: A½ = A , the square root of A,
because (A½)2 = A = (A)2, so A½ = A
because 1 = = A1–1 = A0A1
A1
Negative Power Rule: A–k =
because = A0–k = A–k
1/n - Power Rule: A1/n = A , the nth root of A.
n
(divide–subtract)
(divide–subtract)

97. 0-power Rule: A0 = 1 (A=0)
=
1
Ak
1
Ak
A0
Ak
Special Exponents
½ - Power Rule: A½ = A , the square root of A,
because (A½)2 = A = (A)2, so A½ = A
Example B.
because 1 = = A1–1 = A0A1
A1
Negative Power Rule: A–k =
because = A0–k = A–k
1/n - Power Rule: A1/n = A , the nth root of A.
n
c. 641/3 =
b. 81/3 =
a. 641/2 =
(divide–subtract)
(divide–subtract)

98. 0-power Rule: A0 = 1 (A=0)
=
1
Ak
1
Ak
A0
Ak
Special Exponents
½ - Power Rule: A½ = A , the square root of A,
because (A½)2 = A = (A)2, so A½ = A
Example B.
because 1 = = A1–1 = A0A1
A1
Negative Power Rule: A–k =
because = A0–k = A–k
1/n - Power Rule: A1/n = A , the nth root of A.
n
c. 641/3 =
b. 81/3 =
a. 641/2 = 64 = 8
(divide–subtract)
(divide–subtract)

99. 0-power Rule: A0 = 1 (A=0)
=
1
Ak
1
Ak
A0
Ak
Special Exponents
½ - Power Rule: A½ = A , the square root of A,
because (A½)2 = A = (A)2, so A½ = A
Example B.
because 1 = = A1–1 = A0A1
A1
Negative Power Rule: A–k =
because = A0–k = A–k
1/n - Power Rule: A1/n = A , the nth root of A.
n
c. 641/3 =
b. 81/3 = 8 = 2
3
a. 641/2 = 64 = 8
(divide–subtract)
(divide–subtract)

100. 0-power Rule: A0 = 1 (A=0)
=
1
Ak
1
Ak
A0
Ak
Special Exponents
½ - Power Rule: A½ = A , the square root of A,
because (A½)2 = A = (A)2, so A½ = A
Example B.
because 1 = = A1–1 = A0A1
A1
Negative Power Rule: A–k =
because = A0–k = A–k
1/n - Power Rule: A1/n = A , the nth root of A.
n
c. 641/3 = 64 = 4
3
b. 81/3 = 8 = 2
3
a. 641/2 = 64 = 8
(divide–subtract)
(divide–subtract)

101. Special Exponents
By the power–multiply rule, the fractional exponent
A
k
n±

102. Special Exponents
By the power–multiply rule, the fractional exponent
A
k
n±
(A )n
1
is
take the nth root of A

103. Special Exponents
By the power–multiply rule, the fractional exponent
A
k
n±
(A ) kn ±1
is
take the nth root of A
then raise the
root to ±k power

104. Special Exponents
To calculate a fractional power: extract the root first,
then raise the root to the numerator–power.
By the power–multiply rule, the fractional exponent
A
k
n±
(A ) kn ±1
is
take the nth root of A
then raise the
root to ±k power

105. Special Exponents
a. 9 –3/2 =
To calculate a fractional power: extract the root first,
then raise the root to the numerator–power.
Example C. Find the root, then raise the root to the
numerator–power.
By the power–multiply rule, the fractional exponent
A
k
n±
(A ) kn ±1
is
take the nth root of A
then raise the
root to ±k power
c. 16 -3/4 =
b. 27 -2/3 =

106. Special Exponents
a. 9 –3/2 = (9 ½ * –3)
To calculate a fractional power: extract the root first,
then raise the root to the numerator–power.
Example C. Find the root, then raise the root to the
numerator–power.
By the power–multiply rule, the fractional exponent
A
k
n±
(A ) kn ±1
is
take the nth root of A
then raise the
root to ±k power
c. 16 -3/4 =
b. 27 -2/3 =

107. Special Exponents
a. 9 –3/2 = (9 ½ * –3) = (9½)–3
To calculate a fractional power: extract the root first,
then raise the root to the numerator–power.
Example C. Find the root, then raise the root to the
numerator–power.
By the power–multiply rule, the fractional exponent
A
k
n±
(A ) kn ±1
is
take the nth root of A
then raise the
root to ±k power
c. 16 -3/4 =
b. 27 -2/3 =

108. Special Exponents
a. 9 –3/2 = (9 ½ * –3) = (9½)–3 = (9)–3
To calculate a fractional power: extract the root first,
then raise the root to the numerator–power.
Example C. Find the root, then raise the root to the
numerator–power.
By the power–multiply rule, the fractional exponent
A
k
n±
(A ) kn ±1
is
take the nth root of A
then raise the
root to ±k power
c. 16 -3/4 =
b. 27 -2/3 =

109. Special Exponents
a. 9 –3/2 = (9 ½ * –3) = (9½)–3 = (9)–3 = 3–3
To calculate a fractional power: extract the root first,
then raise the root to the numerator–power.
Example C. Find the root, then raise the root to the
numerator–power.
By the power–multiply rule, the fractional exponent
A
k
n±
(A ) kn ±1
is
take the nth root of A
then raise the
root to ±k power
c. 16 -3/4 =
b. 27 -2/3 =

110. Special Exponents
a. 9 –3/2 = (9 ½ * –3) = (9½)–3 = (9)–3 = 3–3 = 1/27
To calculate a fractional power: extract the root first,
then raise the root to the numerator–power.
Example C. Find the root, then raise the root to the
numerator–power.
By the power–multiply rule, the fractional exponent
A
k
n±
(A ) kn ±1
is
take the nth root of A
then raise the
root to ±k power
c. 16 -3/4 =
b. 27 -2/3 =

111. Special Exponents
a. 9 –3/2 = (9 ½ * –3) = (9½)–3 = (9)–3 = 3–3 = 1/27
To calculate a fractional power: extract the root first,
then raise the root to the numerator–power.
Example C. Find the root, then raise the root to the
numerator–power.
By the power–multiply rule, the fractional exponent
A
k
n±
(A ) kn ±1
is
take the nth root of A
then raise the
root to ±k power
c. 16 -3/4 =
b. 27 -2/3 = (271/3)-2 = (27)-23

112. Special Exponents
a. 9 –3/2 = (9 ½ * –3) = (9½)–3 = (9)–3 = 3–3 = 1/27
To calculate a fractional power: extract the root first,
then raise the root to the numerator–power.
Example C. Find the root, then raise the root to the
numerator–power.
By the power–multiply rule, the fractional exponent
A
k
n±
(A ) kn ±1
is
take the nth root of A
then raise the
root to ±k power
c. 16 -3/4 =
b. 27 -2/3 = (271/3)-2 = (27)-2 = (3)-2 =
3

113. Special Exponents
a. 9 –3/2 = (9 ½ * –3) = (9½)–3 = (9)–3 = 3–3 = 1/27
To calculate a fractional power: extract the root first,
then raise the root to the numerator–power.
Example C. Find the root, then raise the root to the
numerator–power.
By the power–multiply rule, the fractional exponent
A
k
n±
(A ) kn ±1
is
take the nth root of A
then raise the
root to ±k power
c. 16 -3/4 =
b. 27 -2/3 = (271/3)-2 = (27)-2 = (3)-2 = 1/32 = 1/9
3

114. Special Exponents
a. 9 –3/2 = (9 ½ * –3) = (9½)–3 = (9)–3 = 3–3 = 1/27
To calculate a fractional power: extract the root first,
then raise the root to the numerator–power.
Example C. Find the root, then raise the root to the
numerator–power.
By the power–multiply rule, the fractional exponent
A
k
n±
(A ) kn ±1
is
take the nth root of A
then raise the
root to ±k power
c. 16 -3/4 = (161/4)-3 = (16)-34
b. 27 -2/3 = (271/3)-2 = (27)-2 = (3)-2 = 1/32 = 1/9
3

115. Special Exponents
a. 9 –3/2 = (9 ½ * –3) = (9½)–3 = (9)–3 = 3–3 = 1/27
To calculate a fractional power: extract the root first,
then raise the root to the numerator–power.
Example C. Find the root, then raise the root to the
numerator–power.
By the power–multiply rule, the fractional exponent
A
k
n±
(A ) kn ±1
is
take the nth root of A
then raise the
root to ±k power
c. 16 -3/4 = (161/4)-3 = (16)-3 = (2)-34
b. 27 -2/3 = (271/3)-2 = (27)-2 = (3)-2 = 1/32 = 1/9
3

116. Special Exponents
a. 9 –3/2 = (9 ½ * –3) = (9½)–3 = (9)–3 = 3–3 = 1/27
To calculate a fractional power: extract the root first,
then raise the root to the numerator–power.
Example C. Find the root, then raise the root to the
numerator–power.
By the power–multiply rule, the fractional exponent
A
k
n±
(A ) kn ±1
is
take the nth root of A
then raise the
root to ±k power
c. 16 -3/4 = (161/4)-3 = (16)-3 = (2)-3 = 1/23 = 1/84
b. 27 -2/3 = (271/3)-2 = (27)-2 = (3)-2 = 1/32 = 1/9
3

117. a.16–½ =
Fractional Powers
b. 43/2 =
Your turn: calculate the root, then raise the root to the
numerator–power.

118. a.16–½ =
Fractional Powers
b. 43/2 =
Your turn: calculate the root, then raise the root to the
numerator–power.
Ans: ¼, 8

119. a.16–½ =
Fractional Powers
b. 43/2 =
Your turn: calculate the root, then raise the root to the
numerator–power.
Ans: ¼, 8
We use the multiply–add, divide–subtract, and power–
multiply rules to collect fractional exponents.

120. a.16–½ =
Fractional Powers
b. 43/2 =
Your turn: calculate the root, then raise the root to the
numerator–power.
Ans: ¼, 8
We use the multiply–add, divide–subtract, and power–
multiply rules to collect fractional exponents.
x*(x1/3y3/2)2
x–1/2y2/3
=
Example D. Simplify by combining the exponents.

121. a.16–½ =
Fractional Powers
b. 43/2 =
Your turn: calculate the root, then raise the root to the
numerator–power.
Ans: ¼, 8
We use the multiply–add, divide–subtract, and power–
multiply rules to collect fractional exponents.
x*(x1/3y3/2)2
x–1/2y2/3
=
x*x2/3y3
x–1/2y2/3
power–multiply rule
1/3*2 3/2*2
Example D. Simplify by combining the exponents.

122. a.16–½ =
Fractional Powers
b. 43/2 =
Your turn: calculate the root, then raise the root to the
numerator–power.
Ans: ¼, 8
We use the multiply–add, divide–subtract, and power–
multiply rules to collect fractional exponents.
x*(x1/3y3/2)2
x–1/2y2/3
=
x*x2/3y3
x–1/2y2/3
= x–1/2y2/3
x5/3y3
Example D. Simplify by combining the exponents.
power–multiply rule
1/3*2 3/2*2
multiply–add rule
1 + 2/3

123. a.16–½ =
Fractional Powers
b. 43/2 =
Your turn: calculate the root, then raise the root to the
numerator–power.
Ans: ¼, 8
We use the multiply–add, divide–subtract, and power–
multiply rules to collect fractional exponents.
x*(x1/3y3/2)2
x–1/2y2/3
=
x*x2/3y3
x–1/2y2/3
= x–1/2y2/3
=
x5/3y3
x5/3 – (–1/2) y3 – 2/3
Example D. Simplify by combining the exponents.
power–multiply rule
1/3*2 3/2*2
multiply–add rule
1 + 2/3
divide–subtract rule

124. a.16–½ =
Fractional Powers
b. 43/2 =
Your turn: calculate the root, then raise the root to the
numerator–power.
Ans: ¼, 8
We use the multiply–add, divide–subtract, and power–
multiply rules to collect fractional exponents.
x*(x1/3y3/2)2
x–1/2y2/3
=
x*x2/3y3
x–1/2y2/3
= x–1/2y2/3
=
x5/3y3
x5/3 – (–1/2) y3 – 2/3
= x13/6 y7/3
Example D. Simplify by combining the exponents.
power–multiply rule
1/3*2 3/2*2
multiply–add rule
1 + 2/3
divide–subtract rule

125. Fractional Powers
Often it’s easier to manipulate radical–expressions
using the fractional exponent notation.

126. Fractional Powers
Often it’s easier to manipulate radical–expressions
using the fractional exponent notation.
To write a radical in fractional exponent,
assuming a is defined, we have that:k
an = ( a )n → a
k k k
n

127. Fractional Powers
Often it’s easier to manipulate radical–expressions
using the fractional exponent notation.
To write a radical in fractional exponent,
assuming a is defined, we have that:k
an = ( a )n → a
k k k
n
Example E. Write the following expressions using
fractional exponents then simplify if possible.
c. 9 + a2 =
a. 53 or (5 )3 =
b. 9a2 =

128. Fractional Powers
Often it’s easier to manipulate radical–expressions
using the fractional exponent notation.
To write a radical in fractional exponent,
assuming a is defined, we have that:k
an = ( a )n → a
k k k
n
Example E. Write the following expressions using
fractional exponents then simplify if possible.
c. 9 + a2 =
a. 53 or (5 )3 = 53/2
b. 9a2 =

129. Fractional Powers
Often it’s easier to manipulate radical–expressions
using the fractional exponent notation.
To write a radical in fractional exponent,
assuming a is defined, we have that:k
an = ( a )n → a
k k k
n
Example E. Write the following expressions using
fractional exponents then simplify if possible.
c. 9 + a2 =
a. 53 or (5 )3 = 53/2
b. 9a2 = (9a2)1/2

130. Fractional Powers
Often it’s easier to manipulate radical–expressions
using the fractional exponent notation.
To write a radical in fractional exponent,
assuming a is defined, we have that:k
an = ( a )n → a
k k k
n
Example E. Write the following expressions using
fractional exponents then simplify if possible.
c. 9 + a2 =
a. 53 or (5 )3 = 53/2
b. 9a2 = (9a2)1/2 = 3a

131. Fractional Powers
Often it’s easier to manipulate radical–expressions
using the fractional exponent notation.
To write a radical in fractional exponent,
assuming a is defined, we have that:k
an = ( a )n → a
k k k
n
Example E. Write the following expressions using
fractional exponents then simplify if possible.
c. 9 + a2 = (9 + a2)1/2
a. 53 or (5 )3 = 53/2
b. 9a2 = (9a2)1/2 = 3a

132. Fractional Powers
Often it’s easier to manipulate radical–expressions
using the fractional exponent notation.
To write a radical in fractional exponent,
assuming a is defined, we have that:k
an = ( a )n → a
k k k
n
Example E. Write the following expressions using
fractional exponents then simplify if possible.
c. 9 + a2 = (9 + a2)1/2 ≠ (3 + a ).
a. 53 or (5 )3 = 53/2
b. 9a2 = (9a2)1/2 = 3a

133. Fractional Powers
Often it’s easier to manipulate radical–expressions
using the fractional exponent notation.
d. Express a2 (a ) as one radical.3 4
To write a radical in fractional exponent,
assuming a is defined, we have that:k
an = ( a )n → a
k k k
n
Example E. Write the following expressions using
fractional exponents then simplify if possible.
c. 9 + a2 = (9 + a2)1/2 ≠ (3 + a ).
a. 53 or (5 )3 = 53/2
b. 9a2 = (9a2)1/2 = 3a

134. Fractional Powers
Often it’s easier to manipulate radical–expressions
using the fractional exponent notation.
a2 a = a2/3a1/43 4
To write a radical in fractional exponent,
assuming a is defined, we have that:k
an = ( a )n → a
k k k
n
Example E. Write the following expressions using
fractional exponents then simplify if possible.
c. 9 + a2 = (9 + a2)1/2 ≠ (3 + a ).
a. 53 or (5 )3 = 53/2
b. 9a2 = (9a2)1/2 = 3a
d. Express a2 (a ) as one radical.3 4

135. Fractional Powers
Often it’s easier to manipulate radical–expressions
using the fractional exponent notation.
a2 a = a2/3a1/4 = a11/123 4
To write a radical in fractional exponent,
assuming a is defined, we have that:k
an = ( a )n → a
k k k
n
Example E. Write the following expressions using
fractional exponents then simplify if possible.
c. 9 + a2 = (9 + a2)1/2 ≠ (3 + a ).
a. 53 or (5 )3 = 53/2
b. 9a2 = (9a2)1/2 = 3a
d. Express a2 (a ) as one radical.3 4

136. Fractional Powers
Often it’s easier to manipulate radical–expressions
using the fractional exponent notation.
a2 a = a2/3a1/4 = a11/12 = a11
3 4 12
To write a radical in fractional exponent,
assuming a is defined, we have that:k
an = ( a )n → a
k k k
n
Example E. Write the following expressions using
fractional exponents then simplify if possible.
c. 9 + a2 = (9 + a2)1/2 ≠ (3 + a ).
a. 53 or (5 )3 = 53/2
b. 9a2 = (9a2)1/2 = 3a
d. Express a2 (a ) as one radical.3 4

137. Decimal Powers
We write decimal–exponents as fractional exponents,
then we extract roots and raise powers as indicated
by the fractional exponents.

138. Decimal Powers
We write decimal–exponents as fractional exponents,
then we extract roots and raise powers as indicated
by the fractional exponents.
Example F. Write the following decimal exponents as
fractional exponents then simplify, if possible.
a. 9–1.5 =
b. 16–0.75 =
c. 30.4 =

139. Decimal Powers
We write decimal–exponents as fractional exponents,
then we extract roots and raise powers as indicated
by the fractional exponents.
Example F. Write the following decimal exponents as
fractional exponents then simplify, if possible.
a. 9–1.5 = 9 –3/2
b. 16–0.75 =
c. 30.4 =

140. Decimal Powers
We write decimal–exponents as fractional exponents,
then we extract roots and raise powers as indicated
by the fractional exponents.
Example F. Write the following decimal exponents as
fractional exponents then simplify, if possible.
a. 9–1.5 = 9 –3/2 = (9)–3
b. 16–0.75 =
c. 30.4 =

141. Decimal Powers
We write decimal–exponents as fractional exponents,
then we extract roots and raise powers as indicated
by the fractional exponents.
Example F. Write the following decimal exponents as
fractional exponents then simplify, if possible.
a. 9–1.5 = 9 –3/2 = (9)–3 = 3–3 = 1/27
b. 16–0.75 =
c. 30.4 =

142. Decimal Powers
We write decimal–exponents as fractional exponents,
then we extract roots and raise powers as indicated
by the fractional exponents.
Example F. Write the following decimal exponents as
fractional exponents then simplify, if possible.
a. 9–1.5 = 9 –3/2 = (9)–3 = 3–3 = 1/27
b. 16–0.75 = 16 –3/4
c. 30.4 =

143. Decimal Powers
We write decimal–exponents as fractional exponents,
then we extract roots and raise powers as indicated
by the fractional exponents.
Example F. Write the following decimal exponents as
fractional exponents then simplify, if possible.
a. 9–1.5 = 9 –3/2 = (9)–3 = 3–3 = 1/27
b. 16–0.75 = 16 –3/4 = (16)–3
4
c. 30.4 =

144. Decimal Powers
We write decimal–exponents as fractional exponents,
then we extract roots and raise powers as indicated
by the fractional exponents.
Example F. Write the following decimal exponents as
fractional exponents then simplify, if possible.
a. 9–1.5 = 9 –3/2 = (9)–3 = 3–3 = 1/27
b. 16–0.75 = 16 –3/4 = (16)–3 = (2)–3 = 1/8
4
c. 30.4 =

145. Decimal Powers
We write decimal–exponents as fractional exponents,
then we extract roots and raise powers as indicated
by the fractional exponents.
Example F. Write the following decimal exponents as
fractional exponents then simplify, if possible.
a. 9–1.5 = 9 –3/2 = (9)–3 = 3–3 = 1/27
b. 16–0.75 = 16 –3/4 = (16)–3 = (2)–3 = 1/8
4
c. 30.4 = 32/5 = (4)2 ≈ 1.55 (by calculator)
5

146. Decimal Powers
We write decimal–exponents as fractional exponents,
then we extract roots and raise powers as indicated
by the fractional exponents.
Example F. Write the following decimal exponents as
fractional exponents then simplify, if possible.
a. 9–1.5 = 9 –3/2 = (9)–3 = 3–3 = 1/27
b. 16–0.75 = 16 –3/4 = (16)–3 = (2)–3 = 1/8
4
c. 30.4 = 32/5 = (4)2 ≈ 1.55 (by calculator)
5
Working with real numbers and interpreting decimal
exponents as fractions causes problems if the base
is negative.

147. Decimal Powers
We write decimal–exponents as fractional exponents,
then we extract roots and raise powers as indicated
by the fractional exponents.
Example F. Write the following decimal exponents as
fractional exponents then simplify, if possible.
a. 9–1.5 = 9 –3/2 = (9)–3 = 3–3 = 1/27
b. 16–0.75 = 16 –3/4 = (16)–3 = (2)–3 = 1/8
4
c. 30.4 = 32/5 = (4)2 ≈ 1.55 (by calculator)
5
Working with real numbers and interpreting decimal
exponents as fractions causes problems if the base
is negative. For example, (–32)0.2 can be viewed as
(–32)1/5 = –32 = –2, or as (–32)2/10 = (–32)2 which is
not defined.
5 10

148. Exercise A. Write the expressions in radicals and simplify.
1. 41/2 2. 91/2 3. 161/2 4. 251/2
6. 361/2 7. 491/2 8. 641/2 9. 811/2
10. (100x)1/2
x
4( )1/2
11.
9
25( )1/2
12.
13. (–8)1/3
14. –1
64( )1/3
16. 4–1/2 17. 9–1/2 18. 16–1/2 19. 25–1/2
20. 36–1/2 21. 49–1/2 22. 64–1/2 23. 81–1/2
15. 1251/3
x
4( ) –1/2
25.
9
25( ) –1/2
26.
27. –1
64( ) –1/3 28. 125–1/3
x
(24. )–1/2
100
29. 163/2 30. 253/2
31. –1
64( ) –2/3 32. 125–2/3
Fractional Exponents

149. Exercise B. Simplify the expressions by combining the
exponents. Interpret the problems and the results in radicals.
34. x1/2x1/433. x1/3x1/3 35. x1/2x1/3
37.36. 38.x1/3
x1/4 x1/3
x1/3
x1/2
Fractional Exponents
x1/2
Exercise C. Simplify the expressions by combining the
exponents. Leave the answers in simplified fractional
exponents.
40. x1/4x3/2x2/3
39. x1/3x4/3x1/2
45.
48.
y1/2x1/3
x–1/4
x4/3y–3/2
x1/2
41. x3/4y1/2x3/2y4/3
43. y–2/3x–1/4y–3/2x–2/342. y–1/4x5/6x4/3y1/2 44. x3/4y1/2x3/2y4/3
46.
x1/4
x–1/2
47.
x–1/4
x–1/2
49.
y–1/2x1/3
y–4/3x–3/2
50.
(8x2)1/3
(4x)3/2
51.
(27x2)–1/3
(9x)1/2
52.
(100x2)–1/2
(64x)1/3
53.
(36x3)–1/2
(64x1/2)–1/3