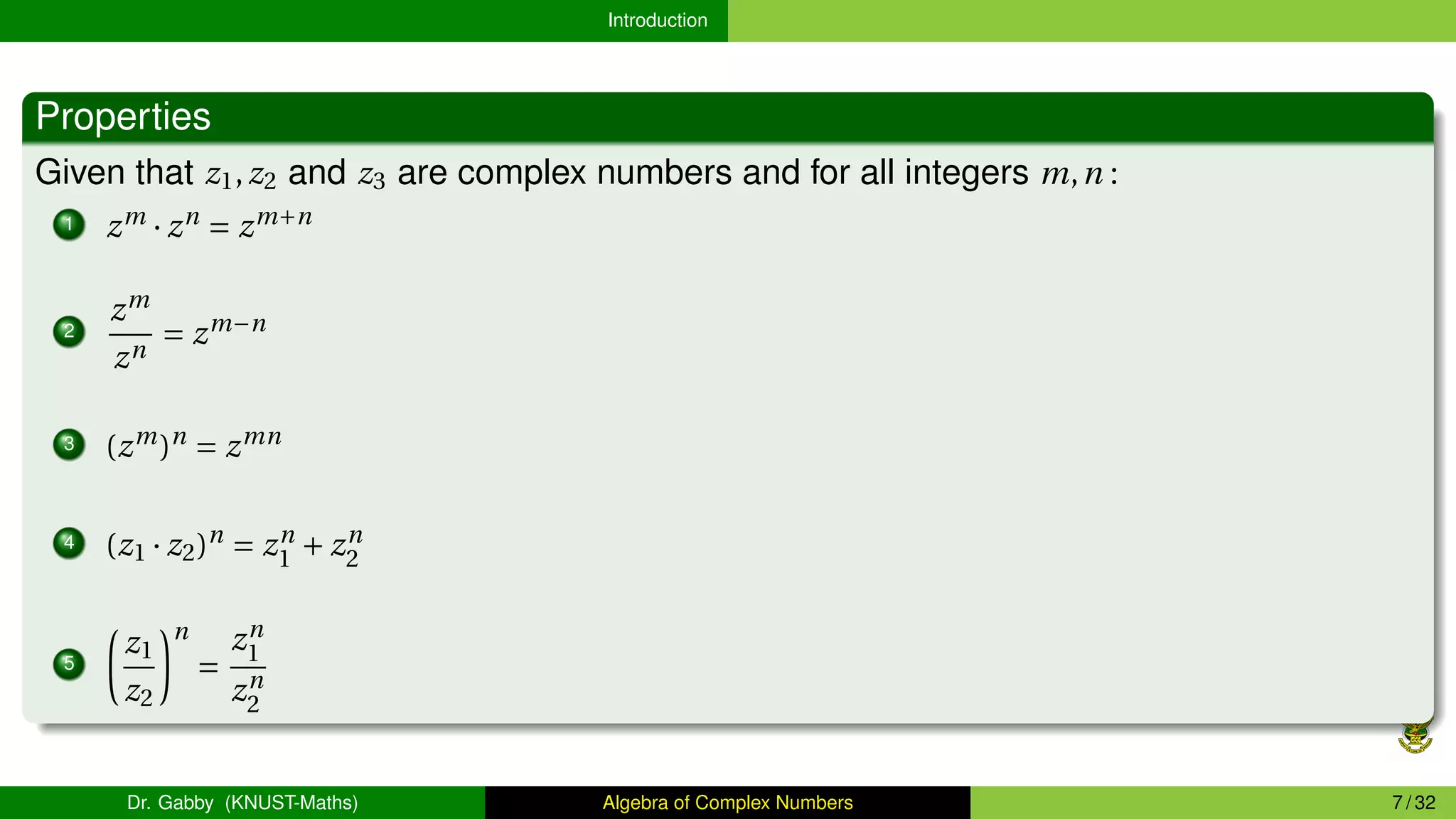
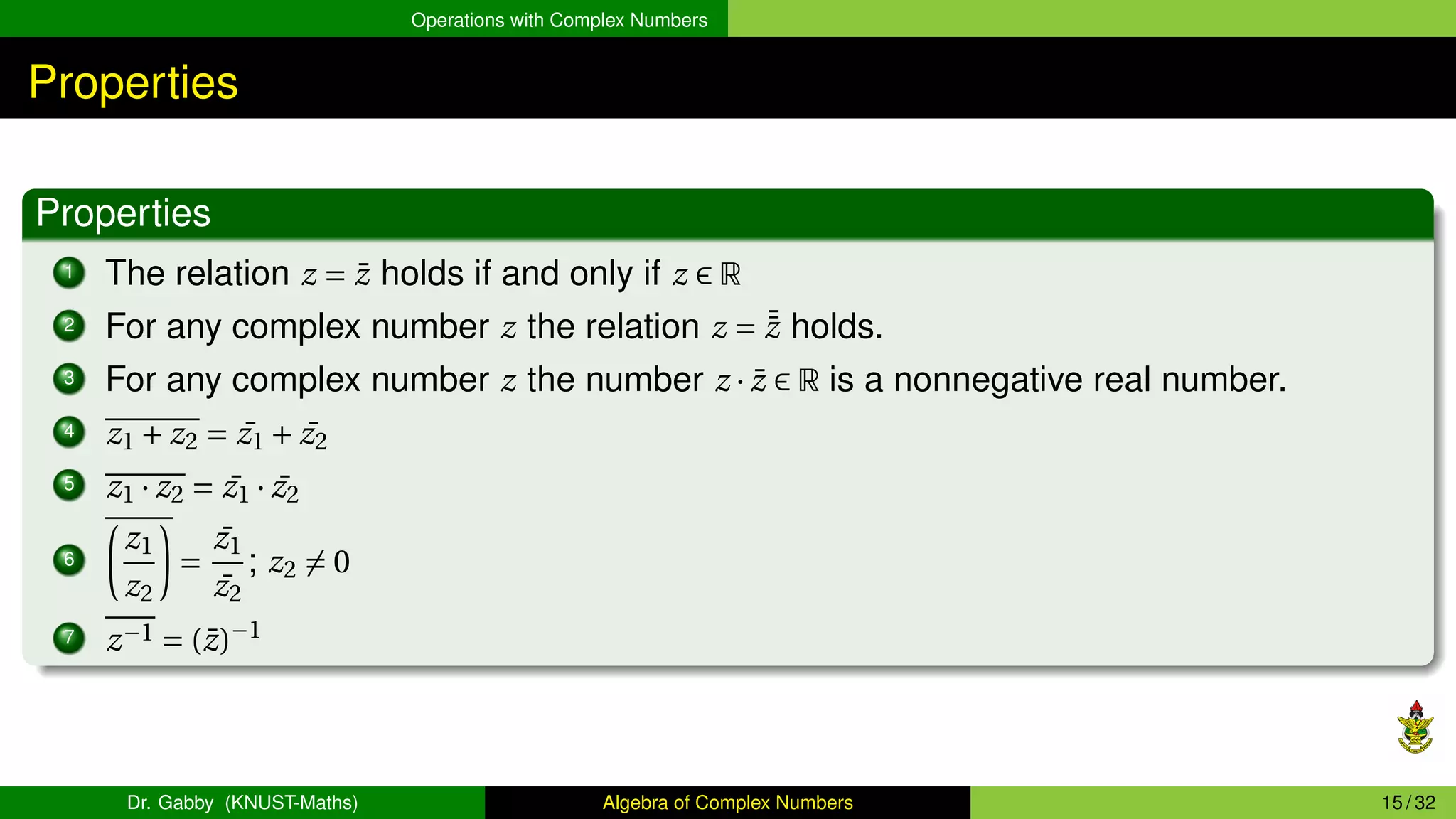
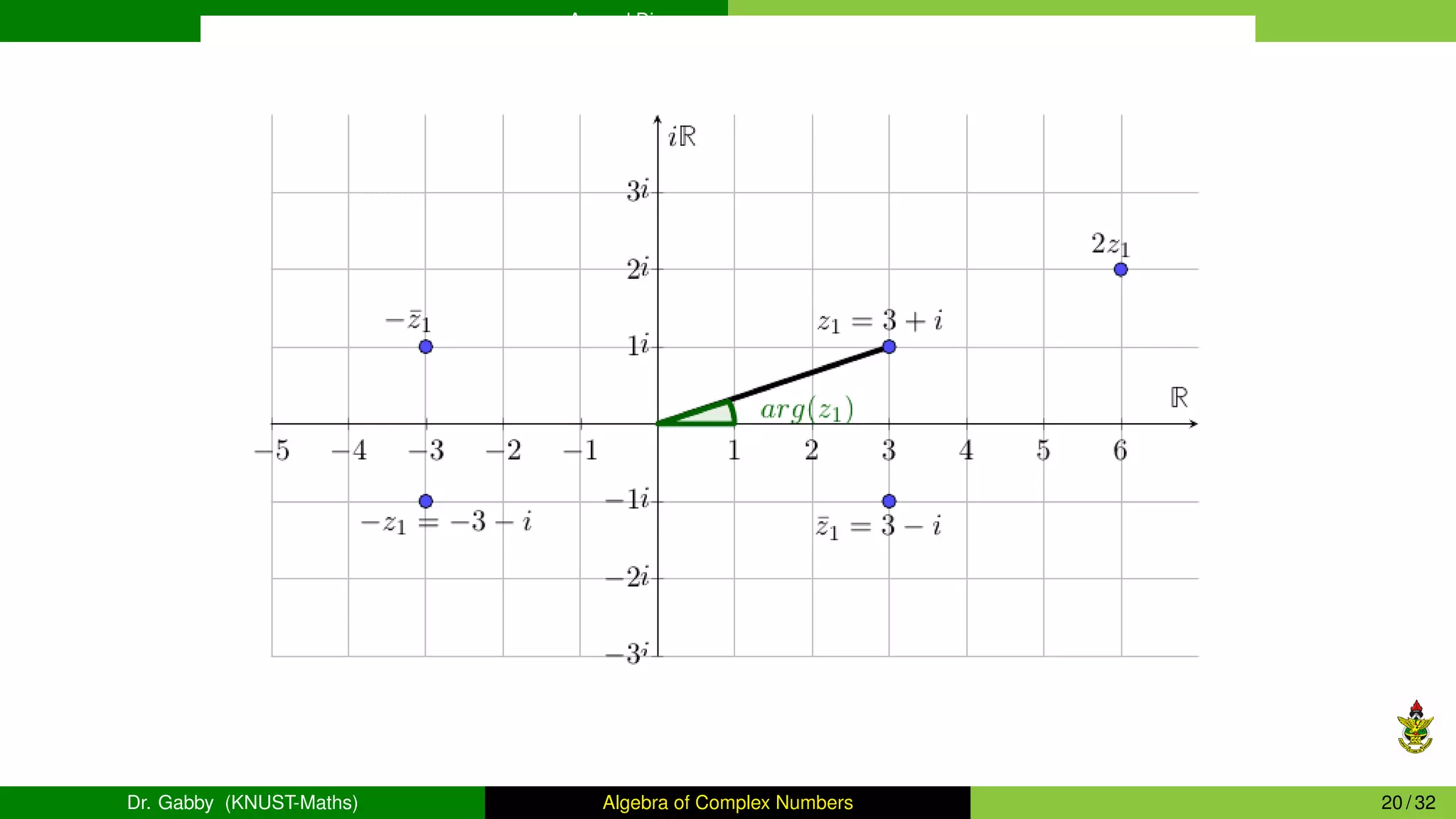
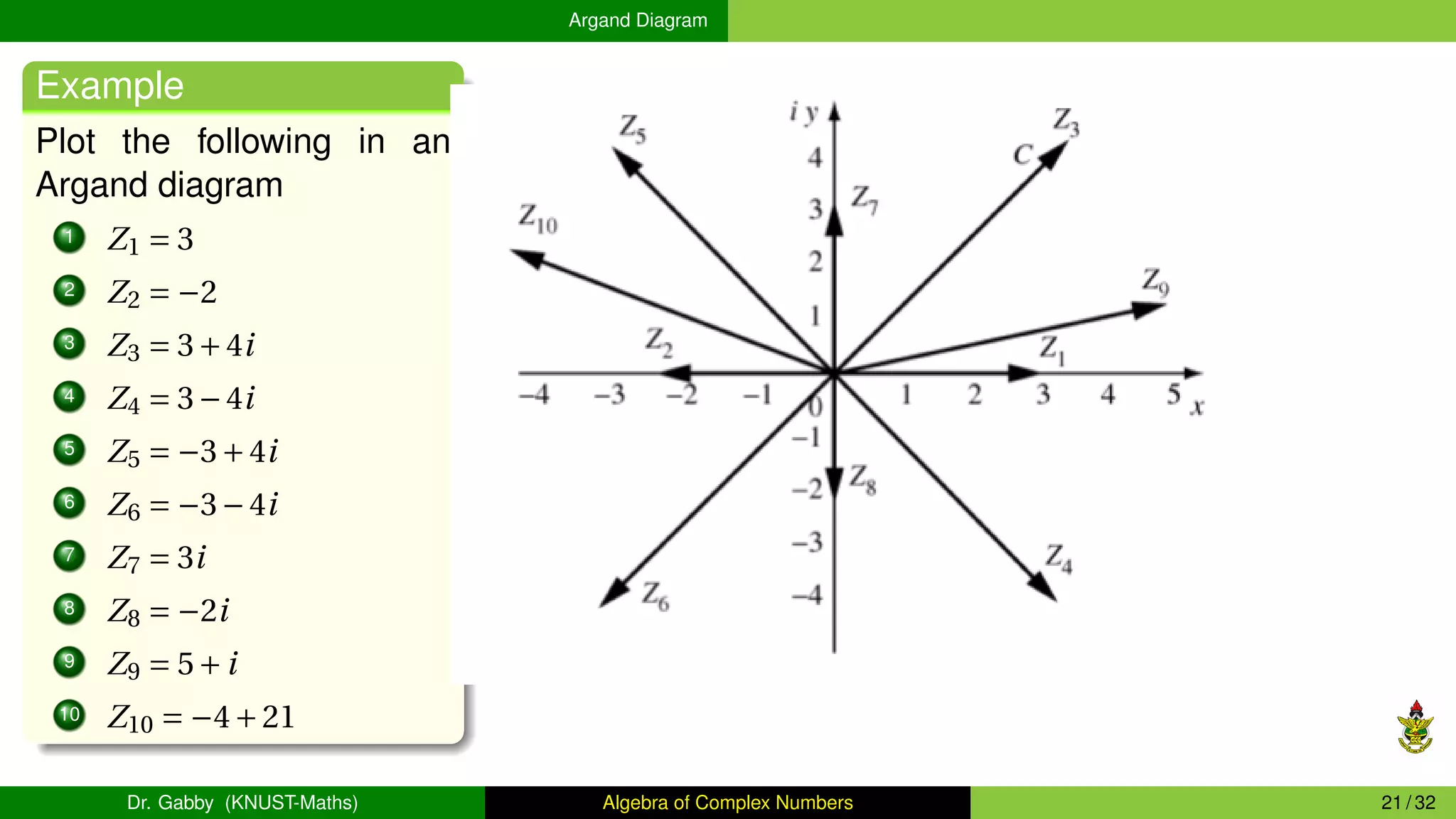
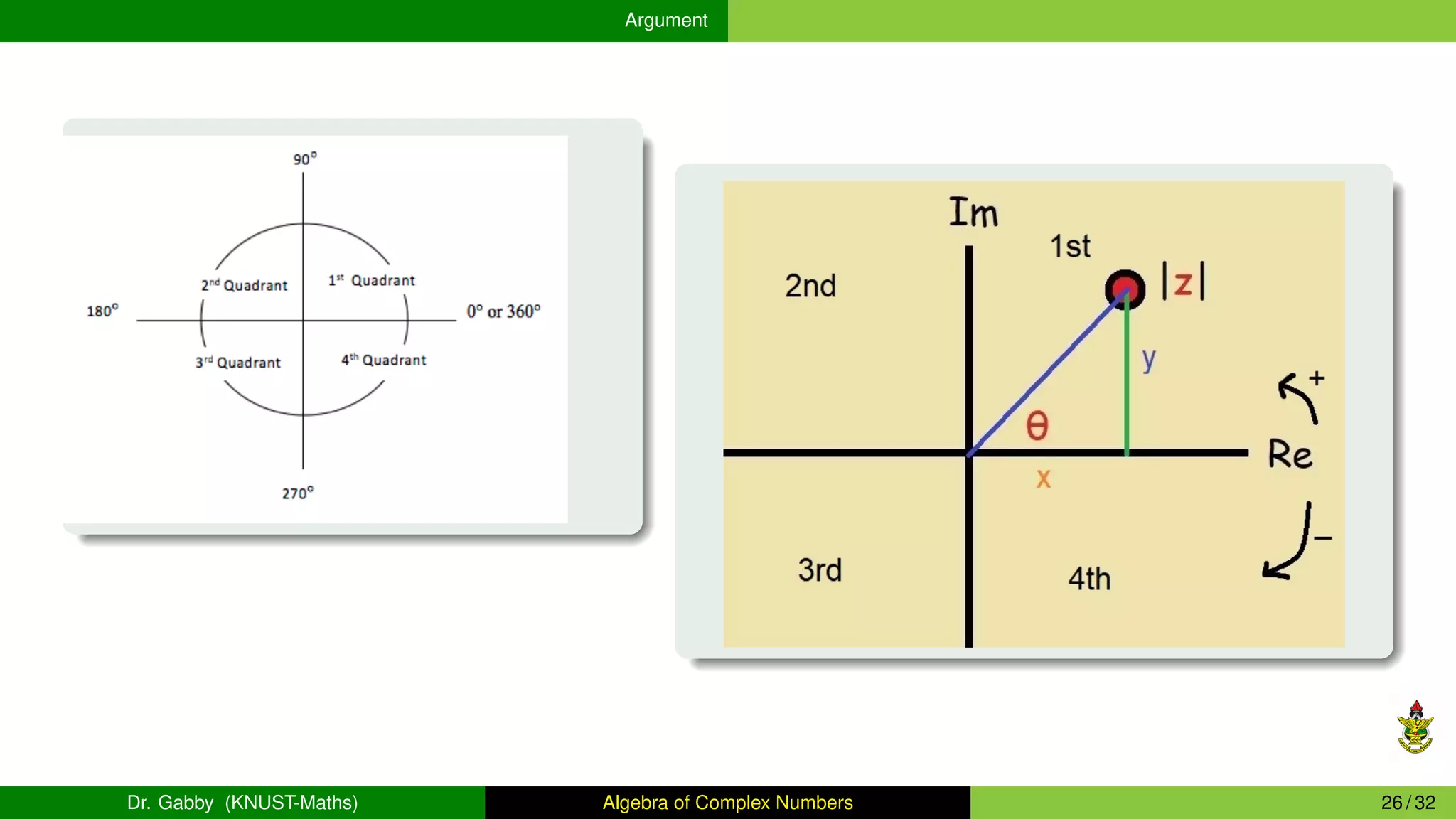
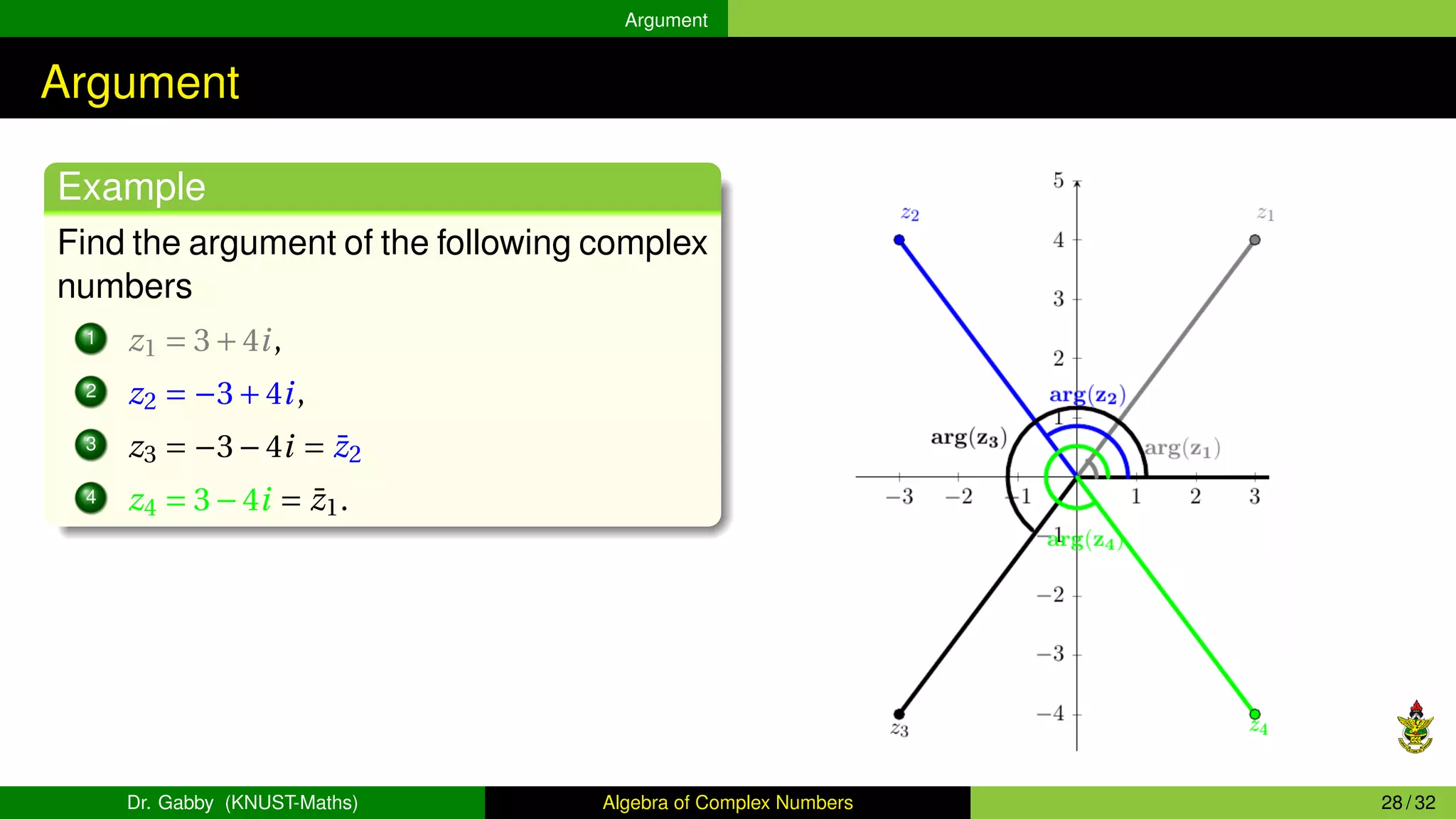
This document provides an overview of the algebra of complex numbers. It begins with an introduction to complex numbers, defining them as numbers of the form a + bi, where a is the real part and b is the imaginary part. It then covers operations with complex numbers like addition, multiplication, and division. Next, it discusses the Argand diagram, which represents complex numbers graphically as points in a plane. It also defines the argument and modulus of a complex number. The document aims to outline the key concepts and operations involving complex numbers.