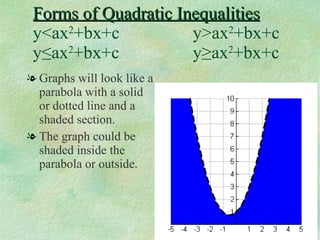
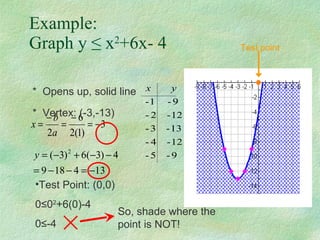
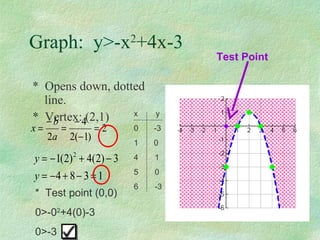
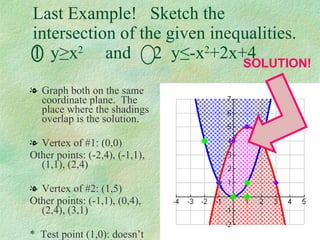
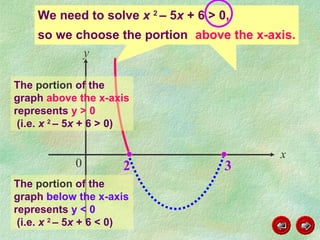
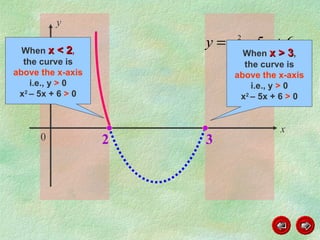
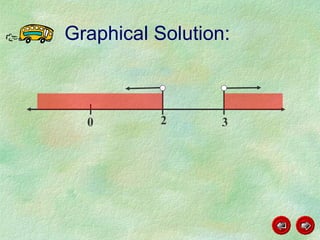
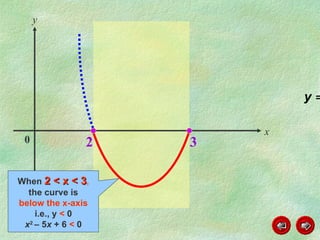
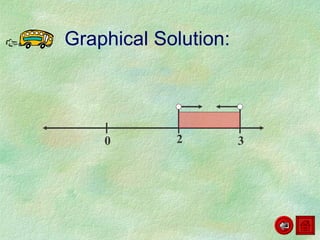
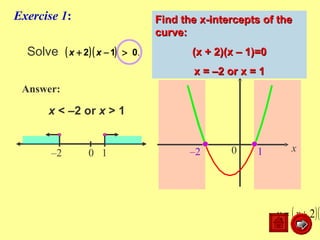
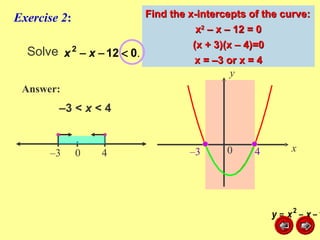
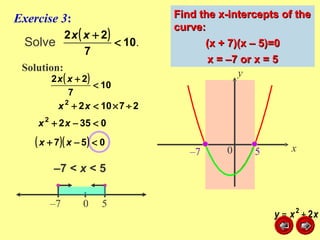
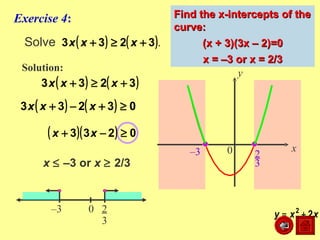
This document discusses how to graph and solve quadratic inequalities. It provides steps for graphing quadratic inequalities by sketching the parabola and shading the appropriate region based on a test point. Examples are given of solving quadratic inequalities graphically by determining the portions of the graph above or below the x-axis and obtaining the solution intervals. Exercises are also worked through to practice solving quadratic inequalities graphically.

1. 6.7 Graph and Solving Quadratic Inequalities

2. Method of Graph sketching

3. Forms of Quadratic Inequalities y<ax 2 +bx+c y>ax 2 +bx+c y ≤ax 2 +bx+c y≥ax 2 +bx+c Graphs will look like a parabola with a solid or dotted line and a shaded section. The graph could be shaded inside the parabola or outside.

4. Steps for graphing 1. Sketch the parabola y=ax 2 +bx+c (dotted line for < or >, solid line for ≤ or ≥) ** remember to use 5 points for the graph! 2. Choose a test point and see whether it is a solution of the inequality. 3. Shade the appropriate region. (if the point is a solution, shade where the point is, if it’s not a solution, shade the other region)

5. Example: Graph y ≤ x 2 +6x- 4 * Vertex: (-3,-13) * Opens up, solid line Test Point: (0,0) 0 ≤0 2 +6(0)-4 0≤-4 So, shade where the point is NOT! Test point

6. Graph: y>-x 2 +4x-3 * Opens down, dotted line. * Vertex: (2,1) * Test point (0,0) 0>-0 2 +4(0)-3 0>-3 x y 0 -3 1 0 1 0 -3 Test Point

7. Last Example! Sketch the intersection of the given inequalities. 1 y ≥x 2 and 2 y≤-x 2 +2x+4 Graph both on the same coordinate plane. The place where the shadings overlap is the solution. Vertex of #1: (0,0) Other points: (-2,4), (-1,1), (1,1), (2,4) Vertex of #2: (1,5) Other points: (-1,1), (0,4), (2,4), (3,1) * Test point (1,0): doesn’t work in #1, works in #2. SOLUTION!

8. Solving Quadratic Inequalities

9. Solve the quadratic inequality x 2 – 5 x + 6 > 0 graphically. Example 1:

10. Procedures: Step (2): we have y = ( x – 2)( x – 3) , i.e. y = 0, when x = 2 or x = 3. Factorize x 2 – 5 x + 6, The corresponding quadratic function is y = x 2 – 5 x + 6 Sketch the graph of y = x 2 – 5 x + 6. Step (1): Step (3): Step (4): Find the solution from the graph.

11. Sketch the graph y = x 2 – 5 x + 6 . What is the solution of x 2 – 5 x + 6 > 0 ? x y 0 y = ( x – 2)( x – 3) ,  y = 0, when x = 2 or x = 3.  2 3

12. x y 0 We need to solve x 2 – 5 x + 6 > 0, The portion of the graph above the x-axis represents y > 0 (i.e. x 2 – 5 x + 6 > 0) The portion of the graph below the x-axis represents y < 0 (i.e. x 2 – 5 x + 6 < 0) above the x-axis. so we choose the portion 2 3

13. x y 0 When x < 2 , the curve is above the x-axis i.e., y > 0 x 2 – 5x + 6 > 0 When x > 3 , the curve is above the x-axis i.e., y > 0 x 2 – 5x + 6 > 0 2 3

14. From the sketch, we obtain the solution or

15. Graphical Solution: 0 2 3

16. Solve the quadratic inequality x 2 – 5 x + 6 < 0 graphically. Example 2: Same method as example 1 !!!

17. x y 0 When 2 < x < 3 , the curve is below the x-axis i.e., y < 0 x 2 – 5 x + 6 < 0 2 3

18. From the sketch, we obtain the solution 2 < x < 3

19. Graphical Solution: 0 2 3

20. Solve Exercise 1 : x < –2 or x > 1 Answer: Find the x-intercepts of the curve: (x + 2)(x – 1)=0 x = –2 or x = 1 x y 0 0 – 2 1 – 2 1

21. Solve Exercise 2 : – 3 < x < 4 Answer: Find the x-intercepts of the curve: x 2 – x – 12 = 0 (x + 3)(x – 4)=0 x = –3 or x = 4 x y 0 0 – 3 4 – 3 4

22. Solve Exercise 3 : – 7 < x < 5 Solution: Find the x-intercepts of the curve: (x + 7)(x – 5)=0 x = –7 or x = 5 x y 0 0 – 7 5 – 7 5

23. Solve Exercise 4 : Solution: Find the x-intercepts of the curve: (x + 3)(3x – 2)=0 x = –3 or x = 2/3 x  –3 or x  2/3 x y 0 – 3 2 3 0 – 3 2 3