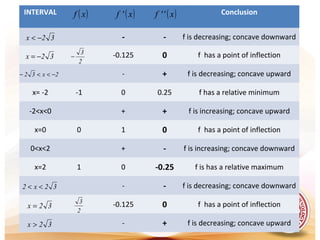
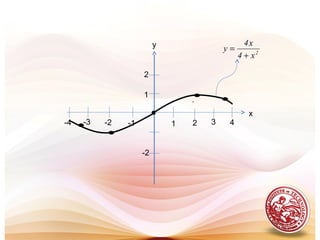
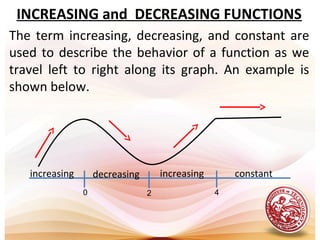
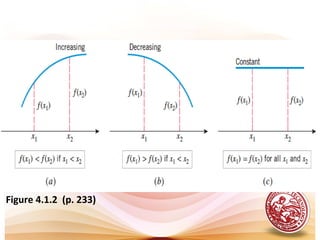
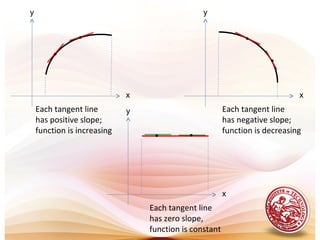
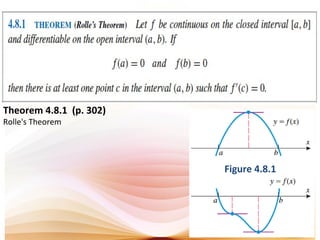
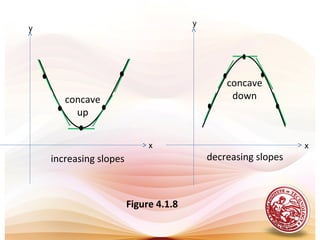
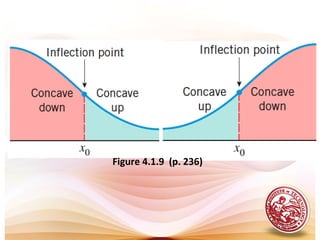
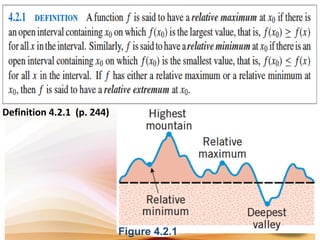
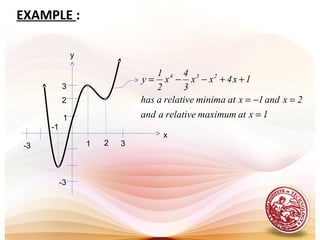
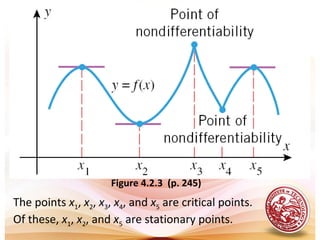
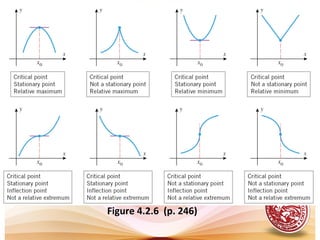
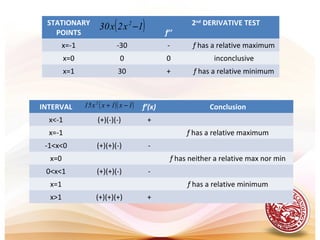
This document discusses analysis of functions including derivatives, extrema, and graphing. It defines key concepts such as increasing and decreasing functions, concavity, points of inflection, stationary points, and relative maxima and minima. It presents Rolle's theorem and the mean value theorem. Examples demonstrate finding critical points and determining the behavior of functions based on the signs of the first and second derivatives. The first and second derivative tests are introduced to identify relative extrema at critical points.

1. THE DERIVATIVE IN
GRAPHING AND
APPLICATIONS

2. ANALYSIS OF FUNCTIONS 1:
INCREASING and DECREASING
FUNCTIONS, ROLLE’S THEOREM,
MEAN VALUE THEOREM, CONCAVITY
and POINT OF INFLECTION

3. OBJECTIVES:
• define increasing and decreasing functions;
•define concavity and direction of bending that is
concave upward or concave downward;
•define Rolle’s Theorem and Mean Value
Theorem; and
• determine the point of inflection.
.

4. 0 2 4
increasing decreasing increasing constant
The term increasing, decreasing, and constant are
used to describe the behavior of a function as we
travel left to right along its graph. An example is
shown below.
INCREASING and DECREASING FUNCTIONS

5. Definition 4.1.1 (p. 233)
The following definition, which is illustrated in
Figure 4.1.2, expresses these intuitive ideas precisely.

6. Figure 4.1.2 (p. 233)

7. y
x
•
•
Each tangent line
has positive slope;
function is increasing
y
x
•
•
Each tangent line
has negative slope;
function is decreasing
y
x
Each tangent line
has zero slope,
function is constant
• •

8. Theorem 4.1.2 (p. 233)

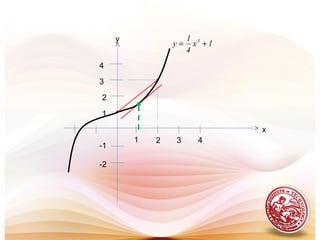
9. .gsindecreaandgsinincreais3x4xf(x)whichonintervalstheFind.1 2
+−=
y
( ) ( )
( ) ( ]
( ) [ )


+∞⇒>>
∞⇒<<
−=−=
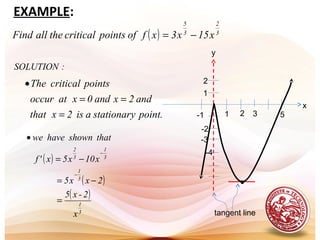
2,onincreasingisf2xwhen0x'f
,2-ondecreasingisf2xwhen0x'f
thus
2x24x2x'f
-1
2
3
x
3x4x)x(f 2
+−=
increasing
decreasing
EXAMPLE:

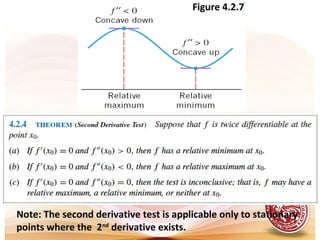
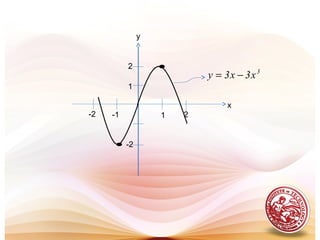
10. .gsindecreaandgsinincreaisxf(x)whichonintervalstheFind.2 3
=
3
x)x(f =
( )
( ) ( ]
( ) [ )


+∞⇒>>
∞⇒<>
=
0,onincreasingisf0xwhen0x'f
,0-onincreasingisf0xwhen0x'f
thus
x3x'f 2
increasing
increasing
y
-4
3
4
x
-3

11. ROLLE’S THEOREM
AND
THE MEAN-VALUE
THEOREM

12. ROLLE’S THEOREM
This theorem states the geometrically obvious
fact that if the graph of a differentiable function
intersects the x-axis at two places, a and b there
must be at least one place where the tangent
line is horizontal.

13. Theorem 4.8.1 (p. 302)
Rolle's Theorem
Figure 4.8.1

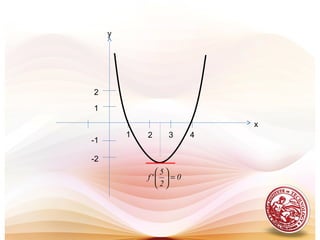
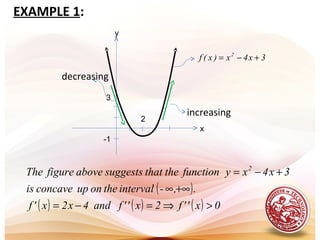
14. EXAMPLE:
Find the two x-intercepts of the function
and confirm that f’(c) = 0 at some point between those
intercepts.
( ) 4x5xxf 2
+−=
Solution:
( ) ( )( )
[ ]
( ) ( )
( )
( ) ( ) .0cf'whichat1,4
intervaltheonpointais
2
5
cso,
2
5
x;05x2xf'
0.cf'thatsuch1,4intervaltheincpointoneleast
atofexistencetheguaranteedareweThus.1,4intervalthe
onsatisfiedareTheoremsRolle'ofhypothesesthe,everywhere
abledifferentiandcontinuousisfpolynomialthesince4x
and1xareintercepts-xtheso,4x1x4x5xxf 2
=
===−=
=
=
=−−=+−=

15. 1 2 3 4
1
2
-1
-2
x
y
0
2
5
'f =






16. THE MEAN-VALUE THEOREM
Rolle’s Theorem is a special case of a more general
result, called the Mean-value Theorem.
Geometrically, this theorem states that between
any two points A (a,f(a)) and B(b,f(b)) on the graph
of a differentiable function f, there is at least one
place where the tangent line to the graph is
parallel to the secant line joining A and B.(Fig 4.8.5)
Figure 4.8.5 (p. 304)

17. Note that the slope of the secant line joining A(a,f(a)) and B(b,f(b)) is
( ) ( )
ab
afbf
m
−
−
=
and that the slope of the tangent line at c in Figure 4.5.8a is f’(c).
Similarly, in Figure 4.5.8b the slopes of the tangent lines at joining
A(a,f(a)) and B(b,f(b)) is
Since nonvertical parallel lines have the same slope, the Mean-Value
Theorem can be stated precisely as follows
( ) ( ) .lyrespective,cf'andcf'arecandc 2121
Theorem 4.8.2 (p. 304)
Mean-Value Theorem

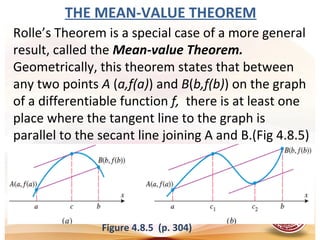
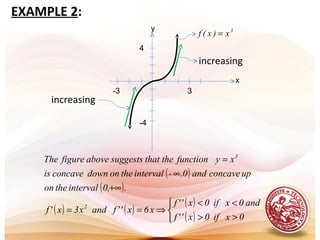
18. EXAMPLE:
Show that the function satisfies the hypotheses
of the mean-value theorem over the interval [0,2], and
find all values of c in the interval (0,2) at which the tangent
line to the graph of f is parallel to the secant line joining
the points (0,f(0)) and (2,f(2)).
( ) 1x
4
1
xf 3
+=
Solution:
[ ] ( )
( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( )
( ).0,2intervaltheinlies1.15only,15.1
3
32
3
4
cTherefore
4c3
02
13
4
c3
ab
afbf
cf'Thus
4
c3
cf'and,
4
x3
xf'32fbf,10fafBut
2.band0awithdsatisfieareTheoremValue-Meantheofhypotheses
theso,0,2onabledifferentiand0,2oncontinuousisfparticularIn
.polynomialaisitbecauseeverywhereiabledifferentandcontinuousisf
2
2
22
+±≈±=±=
=⇒
−
−
=⇒
−
−
=
==⇒====
==

19. 1 2 3 4
1
2
-1
-2
x
y
1x
4
1
y 3
+=
3
4

20. CONCAVITY
Although the sign of the derivative of f reveals where
the graph of f is increasing or decreasing , it does not
reveal the direction of the curvature.
Fig. 4.1.8 suggests two ways to characterize the
concavity of a differentiable f on an open interval:
• f is concave up on an open interval if its tangent lines
have increasing slopes on that interval and is concave
down if they have decreasing slopes.
• f is concave up on an open interval if its graph lies above
its tangent lines and concave down if it lies below its
tangent lines.

21. •
•
•
•
•
concave
up
y
x
••
•
• •concave
down
x
y
increasing slopes decreasing slopes
Figure 4.1.8

22. Formal definition of the “concave up” and “concave
down”.
Definition 4.1.3 (p. 235)

23. Theorem 4.1.4 (p. 235)
Since the slopes of the tangent lines to the graph of a
differentiable function f are the values of its derivative f’,
it follows from Theorem 4.1.2 (applied to f’ rather than f )
that f’ will be increasing on intervals where f’’ is positive
and that f’ will be decreasing on intervals where f’’ is
negative. Thus we have the following theorem.

24. EXAMPLE 1:
( )
( ) ( ) ( ) 0x''f2x''fand4x2x'f
.,-intervaltheonupconcaveis
3x4xyfunctionthethatsuggestsabovefigureThe 2
>⇒=−=
+∞∞
+−=
y
-1
2
3
x
3x4x)x(f 2
+−=
increasing
decreasing

25. EXAMPLE 2:
( )
( )
( ) ( )
( )
( )


>>
<<
⇒==
+∞
∞
=
0xif0x''f
and0xif0x''f
x6x''fandx3x'f
.0,intervaltheon
upconcaveand.0-intervaltheondownconcaveis
xyfunctionthethatsuggestsabovefigureThe
2
3
3
x)x(f =
increasing
increasing
y
-4
3
4
x
-3

26. INFLECTION POINTS
Points where the curve changes from concave up
to concave down or vice-versa are called points of
inflection.
Definition 4.1.5 (p. 236)

27. Figure 4.1.9 (p. 236)

28. 2-1 3
1
2
-3
•
y
x
The figure shows the graph of the function .
Use the 1st
and 2nd
derivatives of f to determine the intervals
on which f is increasing, decreasing, concave up and concave
down. Locate all inflection points and confirm that your
conclusions are consistent with the graph.
( ) 1x3xxf 23
+−=
( ) ( )
( ) ( )1x66x6x''f
2xx3x6x3x'f
:SOLUTION
2
−=−=
−=−=
EXAMPLE 1:

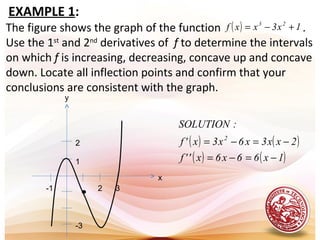
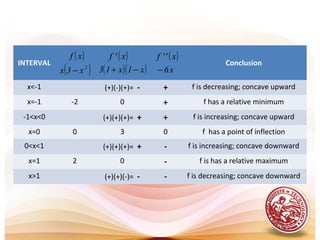
29. INTERVAL (3x)(x-2) f’(x) CONCLUSION
x<0 (-)(-) + f is increasing on
0<x<2 (+)(-) - f is decreasing on
x>2 (+)(+) + f is increasing on
( ]0,∞−
[ ]2,0
[ )+∞,2
INTERVAL (6)(x-1) f’’(x) CONCLUSION
x<1 (-) - f is concave down on
x>1 (+) + f is concave up on ( )+∞,1
( )1,∞−
The 2nd
table shows that there is a point of inflection at x=1,
since f changes from concave up to concave down at that point.
The point of inflection is (1,-1).

30. ( ) .xxfofany,ifpoints,inflectiontheFind 4
=
( )
( )
( )
( ) upconcave;0xwhen0x''f
upconcave0;xwhen0x''f
x12x''f
x4x'f
:SOLUTION
2
3



>>
<>
⇒=
=
( ) .00'f'thougheven0,xatpoint
inflectionnohenceandconcavityinchangenoisthereThus
==
EXAMPLE 2:

31. ANALYSIS OF FUNCTIONS 2:
RELATIVE EXTREMA; GRAPHING
POLYNOMIALS

32. OBJECTIVES:
•define maximum, minimum, inflection,
stationary and critical points, relative maximum
and relative minimum;
•determine the critical, maximum and minimum
points of any given curve using the first and
second derivative tests;
•draw the curve using the first and second
derivative tests; and
•describe the behavior of any given graph in
terms of concavity and relative extrema

33. Definition 4.2.1 (p. 244)
Figure 4.2.1

34. 1xatmaximumrelativeaand
2xand1xatminimarelativeahas
1x4xx
3
4
x
2
1
y 234
=
=−=
++−−=
EXAMPLE :
2
-1
3
1
2
-3
y
x
-3
3
1

35. The points x1, x2, x3, x4, and x5 are critical points.
Of these, x1, x2, and x5 are stationary points.
Figure 4.2.3 (p. 245)

36. Figure 4.2.3 illustrates that a relative extremum
can also occur at a point where a function is not
differentiable.
In general, we define a critical point for a function
f to be a point in the domain of f at which either
the graph of f has a horizontal tangent line or f is
not differentiable (line is vertical).
To distinguish between the two types of critical
points we call x a stationary point of f if f’(x)=0.
Thus we have the following theorem:

37. ( ) 1x3xxfofpointscriticalallFind 3
+−=
( ) ( )( )



=→=−
−=→=+
=−+=−=
1x01x
1x01x
,thus
01x1x33x3x'f
:SOLUTION
2
EXAMPLE 1:
( )
1xand1xatoccur
pointscriticaltheTherefore
1xwhenand
-1xwhen0xf'thatmeansThis
=−=
=
==
tangent line
tangent line

38. ( ) 3
2
3
5
x15x3xfofpointscriticalallFind −=
( ) ( ) ( )




≠→≠
=→=−
=
−
=−=−=
−−
0x0x
2x02x
,thus
0
x
2x5
2xx5x10x5x'f
:SOLUTION
3
1
3
1
3
1
3
1
3
2
( )
( )
point.rystationaais2xthat
and2xand0xatoccur
pointscriticaltheTherefore
0xwhenxf'and
2xwhen0xf'thatmeansThis
=
==
=∞=
==
52-1 3
-4
1
-3
y
x
-2
2
1
•
tangent line
EXAMPLE 2:

39. FIRST DERIVATIVE TEST
Theorem 4.2.2 asserts that the relative extrema
must occur at critical points, but it does not say
that a relative extremum occurs at every critical
point.
sign.changesf'wherepointscritical
thoseatextremumrelativeahasfunctionA

40. Figure 4.2.6 (p. 246)

41. Theorem 4.2.3 (p. 247) First Derivative Test
•The above theorem simply say that for a continuous
function, relative maxima occur at critical points
where the derivative changes from (+) to (–) and
relative minima where it changes from (–) to (+).

42. EXAMPLE:
( ) 3
2
3
5
x15x3xfofpointscriticaltheallFind −=
:SOLUTION
point.ystationarais2xthat
and2xand0xatoccur
pointscriticalThe
=
==
•
( )
( )
( )
3
1
3
1
3
1
3
2
x
2-x5
2xx5
x10x5x'f
thatshownhavewe
=
−=
−=
•
−
−
52-1 3
-4
1
-3
y
x
-2
2
1
•
tangent line

43. :belowshownisderivativethisofanalysissignA
INTERVAL f’(x)
x<0 (-)/(-) +
0<x<2 (-)/(+) _
x>2 (+)/(+) +
( ) 3
1
x/2x5 −
imumminrelative2xattofromchangesf'ofsignThe
imummaxrelative0xattofromchangesf'ofsignThe
→=+−
→=−+

44. SECOND DERIVATIVE TEST
There is another test for relative extrema that is based on
the following geometric observation:
• A function f has a relative maximum at stationary point
if the graph of f is concave down on an open interval
containing that point.
•A function f has a relative minimum at stationary point if
the graph of f is concave up on an open interval
containing that point.

45. Note: The second derivative test is applicable only to stationary
points where the 2nd
derivative exists.
Figure 4.2.7

46. EXAMPLE:
( ) 35
x5x3xfofextremarelativetheFind.1 −=
:SOLUTION
( ) ( ) ( )( )
( ) ( )( )
( ) ( )
( ) ( )12x30x30x-60xx''f
1x-1;x0;x
01x;01x;015x
01x1x15x0x'fwhen
1x1x15x1x15x15x-15xx'f
23
2
2
22224
−==
===
=−=+=
=−+→=
−+=−==

47. STATIONARY
POINTS f’’
2nd
DERIVATIVE TEST
x=-1 -30 - f has a relative maximum
x=0 0 0 inconclusive
x=1 30 + f has a relative minimum
( )1x2x30 2
−
INTERVAL f’(x) Conclusion
x<-1 (+)(-)(-) +
x=-1 f has a relative maximum
-1<x<0 (+)(+)(-) -
x=0 f has neither a relative max nor min
0<x<1 (+)(+)(-) -
x=1 f has a relative minimum
x>1 (+)(+)(+) +
( )( )1x1xx15 2
−+

48. 2-1
1
y
x
-2
2
1
•
•

49. 3
xx3yofcurvethetraceandAnalyze.2 −=
( ) ( )( )
( ) ( )
1xand-1x
0x1and0x1
0x1x13x-13
x33'y
xx3y
2
2
3
==
=−=+
=−+=
−=
−=
0x
0x6
x6''y
=
=−
−=
:SOLUTION

50. INTERVAL Conclusion
x<-1 (+)(-)(+)= - + f is decreasing; concave upward
x=-1 -2 0 + f has a relative minimum
-1<x<0 (+)(+)(+)= + + f is increasing; concave upward
x=0 0 3 0 f has a point of inflection
0<x<1 (+)(+)(+)= + - f is increasing; concave downward
x=1 2 0 - f is has a relative maximum
x>1 (+)(+)(-)= - - f is decreasing; concave downward
( )
( )2
x3x
xf
−
( )
( )( )x1x13
x'f
−+
( )
x6
x''f
−

51. -2
•
•
2-1
1
y
x
-2
2
1
3
x3x3y −=

52. 2
x4
x4
yofcurvethetraceandAnalyze.3
+
=
( )( ) ( )
( )
( ) ( )
( )
( )
( )( )
( )
( ) ( )
2xand-2x
0x2and0x2
0
x4
x2x24
x4
x44
'y
x4
x416
x4
x8x416
'y
x4
x2x44x4
'y
x4
x4
y
2222
2
22
2
22
22
22
2
2
==
=−=+
=
+
−+
=
+
−
=
+
−
=
+
−+
=
+
−+
=
+
=

53. ( )( ) ( )( )( )( )
( )
( ) ( ) ( )( )
( ) ( ) ( )[ ]
( )( )
( )( )
( )( )
32xand0x
012xx4x8
024x2x44x-
016x4x28x44x-
016x4x42x44x-
016x4x4x4x8x4
x4
x2x4216x4x8x4
''y
22
22
222
222
2222
42
222
±==
=−+
=+−+
=+−++
=+−+++
=+−+−−+
+
++−−−+
=

54. INTERVAL Conclusion
- - f is decreasing; concave downward
-0.125 0 f has a point of inflection
- + f is decreasing; concave upward
x= -2 -1 0 0.25 f has a relative minimum
-2<x<0 + + f is increasing; concave upward
x=0 0 1 0 f has a point of inflection
0<x<2 + - f is increasing; concave downward
x=2 1 0 -0.25 f is has a relative maximum
- - f is decreasing; concave downward
-0.125 0 f has a point of inflection
- + f is decreasing; concave upward
( )xf ( )x'f ( )x''f
32x −<
32x −=
2x32 −<<−
32x2 <<
32x >
32x =
2
3
−
2
3

55. -2
•
•
2-1
1
y
x
-2
2
1-3-4 3 4
`
2
x4
x4
y
+
=
•
•

56. 7x12x3x2y.1 23
+−+=
4x
2
y.2 2
−
=
234
x12x4x3y.3 −−=
2
2
x
1
xy.4 +=
35
x
3
2
x
5
1
y.5 −=
234
x6x8x3y.6 +−=
)x2(xy.7 22
−=
( )2
x1
x
y.8
−
=
Exercises:
Determine any critical points, point of inflection and
trace the curve.