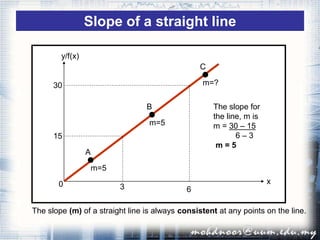
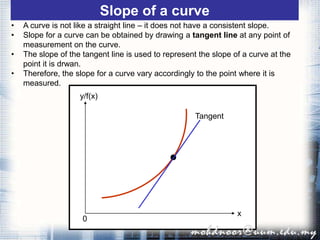
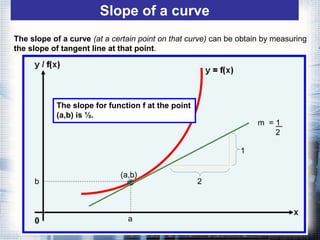
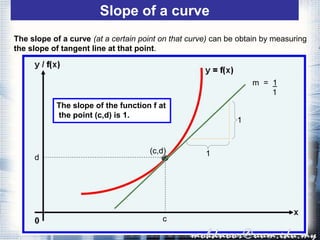
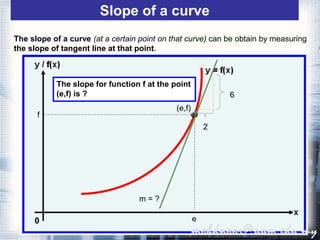
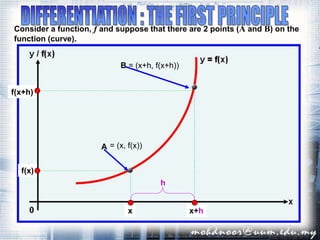
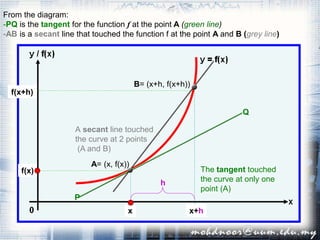
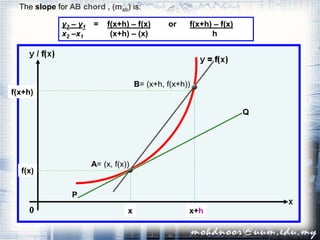
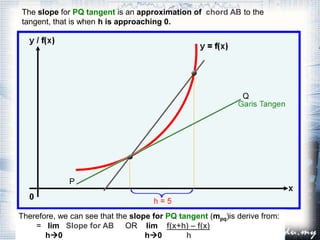
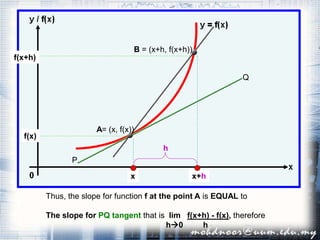
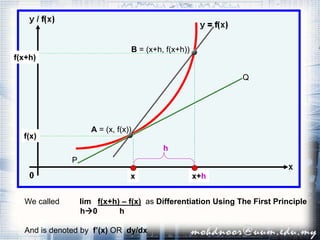
1. The document discusses the concept of the derivative and differentiation using the first principle. It explains how to calculate the slope of a tangent line to a curve at a point using limits, which gives the derivative of the function at that point. 2. Rules for differentiating common functions like polynomials, exponentials, and logarithms are covered. Higher-order derivatives and applications of derivatives to business and economics are also mentioned. 3. The goals of the class are to explain the concept of the derivative, differentiate functions using the first principle (limits), and understand various differentiation rules.

1. C H A P T E R 7 :
Mohd Noor Abdul Hamid, Ph.D

2. 1. The concept of derivative
- Notation
- First Principle of Differentiation
2. Rules of Differentiation for:
- Derivative of a Constant
- Derivative of xn
- Constant Factor Rule
- Derivative of a Sum or Differences
- Product & Quotient Rules
- Chain Rule and Power Rule
- Exponent & Logarithmic Rules
3. Higher order of derivatives
• Critical points – minimum, maximum, inflection point
• Application : Business and economics

3. After finishing this class, you should be able to:
• Explain the concept of derivative.
• Differentiate a function using the First Principle
(The Concept of limit)

4. The concepts of derivative : Notation
If f defined as the function of x and can be written as f(x).
Then the derivative of f(x) = y denoted as f’(x) or is read as
“derivative value of function f at x”.
The process to get f’(x) is called DIFFERENTIATION
(FIRST DERIVATIVE)
dx
dy
f(x)
g(u)
y = f(x)
U = f(v)
f’(x)differentiate
g’(u)differentiate
dy
dx
differentiate
dU
dv
differentiate

6. y/f(x)
x
3 6
15
30
0
Slope of a straight line
The slope for
the line, m is
m = 30 – 15
6 – 3
m = 5
m=5
A
m=5
B
m=?
C
The slope (m) of a straight line is always consistent at any points on the line.

7. Slope of a curve
• A curve is not like a straight line – it does not have a consistent slope.
• Slope for a curve can be obtained by drawing a tangent line at any point of
measurement on the curve.
• The slope of the tangent line is used to represent the slope of a curve at the
point it is drwan.
• Therefore, the slope for a curve vary accordingly to the point where it is
measured.
0
y/f(x)
x
Tangent

8. The slope of a curve (at a certain point on that curve) can be obtain by measuring
the slope of tangent line at that point.
m = 1
2
1
2
a
b
(a,b)
The slope for function f at the point
(a,b) is ½.
Slope of a curve

9. The slope of the function f at
the point (c,d) is 1.
1
1
m = 1
1
c
d
(c,d)
The slope of a curve (at a certain point on that curve) can be obtain by measuring
the slope of tangent line at that point.
Slope of a curve

10. The slope for function f at the point
(e,f) is ? 6
2
m = ?
e
f
(e,f)
The slope of a curve (at a certain point on that curve) can be obtain by measuring
the slope of tangent line at that point.
Slope of a curve

11. x
h
x+h
f(x)
f(x+h)
Consider a function, f and suppose that there are 2 points (A and B) on the
function (curve).
A
B
= (x, f(x))
= (x+h, f(x+h))

12. x
h
x+h
f(x)
f(x+h)
A= (x, f(x))
B= (x+h, f(x+h))
The tangent touched
the curve at only one
point (A)
A secant line touched
the curve at 2 points
(A and B)
From the diagram:
-PQ is the tangent for the function f at the point A (green line)
-AB is a secant line that touched the function f at the point A and B (grey line)
P
Q

13. P
Q
The slope for AB chord , (mab) is:
f(x)
f(x+h)
A= (x, f(x))
B= (x+h, f(x+h))
y2 – y1 = f(x+h) – f(x) or f(x+h) – f(x)
x2 –x1 (x+h) – (x) h
x x+h

14. The slope for PQ tangent is an approximation of chord AB to the
tangent, that is when h is approaching 0.
P
Q
Therefore, we can see that the slope for PQ tangent (mpq)is derive from:
= lim Slope for AB OR lim f(x+h) – f(x)
h0 h0 h

15. x
h
x+h
f(x)
f(x+h)
A
B
= (x, f(x))
= (x+h, f(x+h))
P
Q
Thus, the slope for function f at the point A is EQUAL to
The slope for PQ tangent that is lim f(x+h) - f(x), therefore
h0 h

16. x
h
x+h
f(x)
f(x+h)
A
B
= (x, f(x))
= (x+h, f(x+h))
P
Q
We called lim f(x+h) – f(x) as Differentiation Using The First Principle
h0 h
And is denoted by f’(x) OR dy/dx

17. DIFFERENTIATION : USING THE FIRST PRINCIPLE
dy = f’(x) = lim f(x+h) – f(x)
dx h0 h