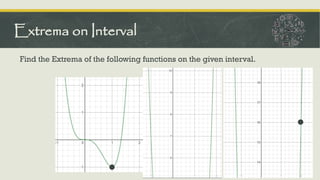
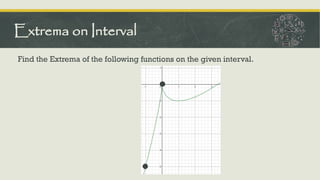
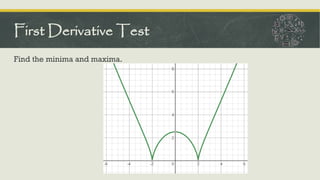
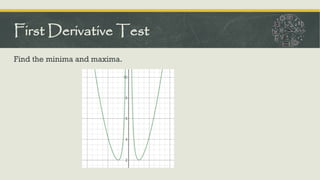
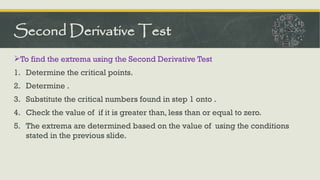
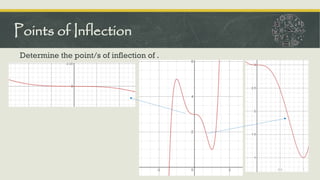
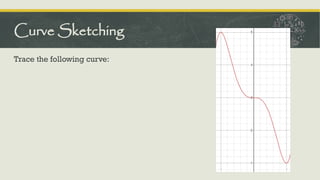
The document outlines the concepts of critical numbers and critical points in polynomial functions, emphasizing their importance in determining extrema, including both relative and absolute maxima and minima. It details methods for finding critical points through derivatives and the subsequent steps to ascertain extrema within an interval, utilizing both first and second derivative tests. Additionally, it describes the procedure for sketching polynomial curves by identifying intersection points with axes and analyzing concavity and points of inflection.

1. POLYNOMIAL CURVES

2. Critical Numbers
Let be defined at . If or if is undefined at , then is a critical number of .
Note that we require that exists in order for to actually be a critical
number.This is an important, and often overlooked, number.What this is really
saying is that all critical numbers must be in the domain of the function. If a
number is not in the domain of the function then it is not a critical number.
Sometimes critical number and critical point are loosely used
interchangeably, but typically when you're asked to identify a critical point,
you're expected to provide the coordinates of the point (both and ), and a
critical number is just the value: the place on the number line where is zero or
undefined.
Critical Points

3.  To find the Critical Points
1. Find the first derivative of the given function.
2. Express the right side of the first derivative equation into factors.
3. Equate to zero and use the zero-factor property to solve for values which are
called the critical numbers.
4. In cases where factors in the right side involves fractions, critical numbers
are those values of that will make the value of to be undefined.
5. Find the value of by substituting the critical numbers found in step 3 and/or
step 4 to the given original function.
6. The coordinates that will be formed are called the critical points.
Critical Points

4. Find the critical points of the function
CN:
Critical Points
CP:

5. Find the critical points of the function .
Critical Points
0 =
0 =
CN:
CP: :

6. Extrema or Extreme - a term used to collectively refer to the maxima and
minima of a function
Relative Extrema - a term used to collectively refer to relative maxima and
minima
Relative Maximum - a maximum that is greater than any other in the
neighborhood
Relative Minimum - the lesser value than any other in the neighborhood
Absolute Maximum - the greatest value that the function can assume anywhere
in its range
Absolute Minimum - the lowest value that the function can assume anywhere in
its range
Extrema on Interval

7. To find the extrema:
1. Get the critical points.
2. Substitute the left and right endpoints of the interval to the given original
function to find the values of of the corresponding endpoints.
3. Compare the points found in steps 1 and 2.The lowest among the values will
be the minimum number and the highest among the values will be the
maximum number.
4. The ordered pair formed by these minimum and maximum numbers will
correspond to the minimum and maximum points, respectively.These are
called the extrema of the given functions.
Extrema on Interval

8. Find the Extrema of the following functions on the given interval.
Extrema on Interval
CN:
CP:
CP:
Endpoints:

9. Find the Extrema of the following functions on the given interval.
Extrema on Interval

10. Find the Extrema of the following functions on the given interval.
Extrema on Interval
From previous example
Critical Points: ,
Endpoints:

11. Find the Extrema of the following functions on the given interval.
Extrema on Interval

12. First Derivative Test
At a point where ,
-if changes from positive to negative (as increases), is maximum
-if changes from negative to positive, is a minimum
-if does not change sign, is neither a maximum nor a minimum
Note: When using the 1st
Derivative Test, be sure to consider the domain of the
function. (the value of that will make undefined)
First Derivative Test

13. To find the extrema using the First Derivative Test:
1. Determine the critical points.
2. Make a table of 4 rows to test the intervals based on the critical numbers
found in step 1.
Intervals:
Test Value:
Sign of :
Conclusion:
Note: and
First Derivative Test

14. Find the minima and maxima.
First Derivative Test

15. Find the minima and maxima.
First Derivative Test

16. Find the minima and maxima.
First Derivative Test

17. Find the minima and maxima.
First Derivative Test

18. At a point where , and :
-if , is increasing, the curve is concave
upward, assumes the minimum value as
increases
-if , is decreasing, the curve is concave
downward, assumes the maximum value
as increases
Concavity

19. Second Derivative Test
At a point where ,
-if , is a minimum;
-if , is a maximum;
-if , the test fails: use the 1st
Derivative Test to find the maximum and minimum
point
Second Derivative Test

20. To find the extrema using the Second Derivative Test
1. Determine the critical points.
2. Determine .
3. Substitute the critical numbers found in step 1 onto .
4. Check the value of if it is greater than, less than or equal to zero.
5. The extrema are determined based on the value of using the conditions
stated in the previous slide.
Second Derivative Test

21. Examine the following functions for maxima and minima:
Second Derivative Test
From example 5c:
Critical Points: ,

22. Point of Inflection
-is a point at which the curve changes from concave upward to concave
downward or vice versa
-is a point at which vanishes provided changes sign at that point; if vanishes
without changing sign, it is not a point of inflection
Note:
A point where is a maximum or a minimum provided If and both equal to
zero, the point is in general a point of inflection with a horizontal tangent; but if
vanishes without changing sign, the point is a maximum or a minimum.
Points of Inflection

23. Determine the point/s of inflection of .
Points of Inflection

24. .
Points of Inflection

25. Determine the point/s of inflection of .
Points of Inflection

26. Determine the point/s of inflection of .
Points of Inflection

27. Steps in sketching polynomial curves
1. Find the points of intersection with the axes.
2. Find the first derivative and equate it to zero. Solve to find the abscissa of the
maximum and minimum points.Test these values.
3. Find the second derivative and equate to zero. Solve to find the abscissas of
the points of inflection. Test the values.
4. Calculate the corresponding ordinates of the points whose abscissas were
found in the 2nd
and 3rd
steps. Calculate more points as necessary.
5. Plot and sketch the curve.
Curve Sketching

28. Trace the following curve:
Curve Sketching
From previous example :
Critical Points: , ,
Points of Inflection: , ,

29. Trace the following curve:
Curve Sketching