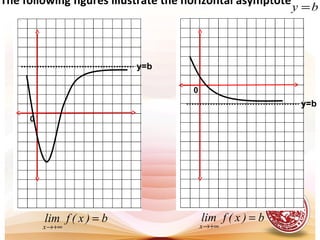
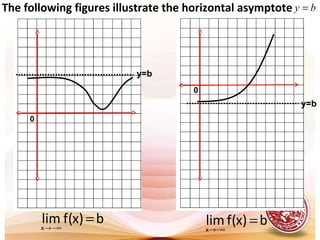
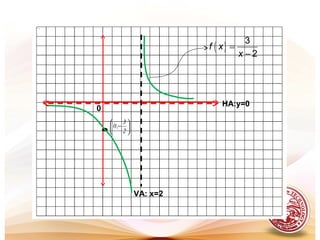
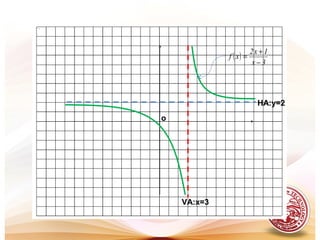
This document discusses limits of functions, including infinite limits, vertical and horizontal asymptotes, and the squeeze theorem. It provides definitions and examples of:
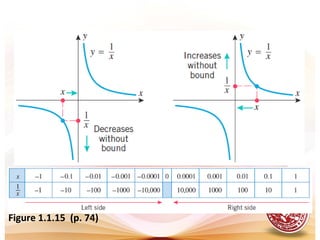
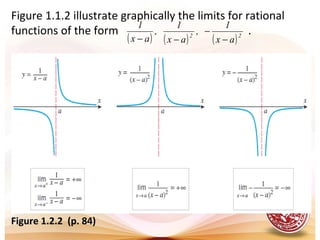
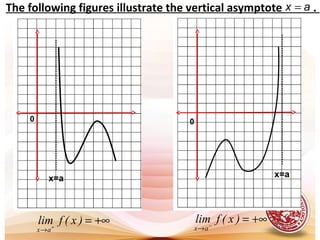
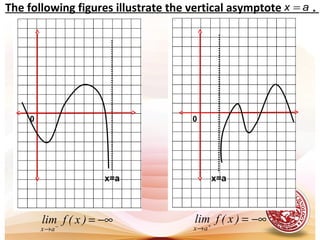
- Infinite limits, where the value of a function increases or decreases without bound as the input approaches a number.
- Vertical and horizontal asymptotes, which are lines that a function approaches but does not meet as the input increases or decreases without limit.
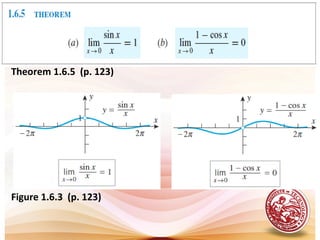
- The squeeze theorem, which can be used to evaluate limits where usual algebraic methods are not effective by "squeezing" the function between two other functions with known limits. Examples demonstrate how to apply this theorem.