Increasing decreasing functions
•Download as PPT, PDF•
0 likes•2,066 views
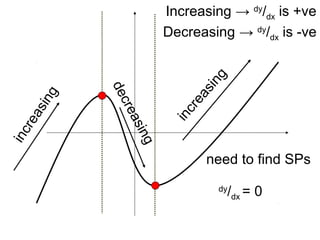
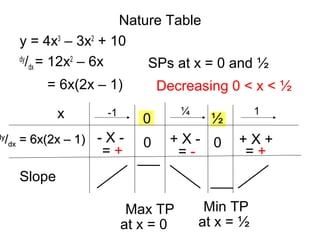
The document discusses increasing and decreasing functions. It defines an increasing function as one where the gradient (dy/dx) is always positive, and a decreasing function as one where the gradient is always negative. To determine if a function is increasing or decreasing, you find where the derivative (dy/dx) is equal to 0 to find critical points, and use a nature table to analyze the sign of the derivative on each interval. The derivative also needs to be analyzed to determine if a function is always increasing or decreasing.
Report
Share
Report
Share
Recommended
27 power series x
I. A power series is a "polynomial" with infinitely many terms of the form P(x) = Σn=0∞ anxn.
II. The radius of convergence R determines the values of x where the power series converges or diverges: it converges absolutely for |x| < R, diverges for |x| > R, and may converge or diverge at x = ±R.
III. The ratio test and root test can be used to calculate the radius of convergence R.
21 lagrange multipliers
The document describes Lagrange multipliers, which are used to find the extrema (maximum and minimum points) of a function subject to a constraint. Specifically:
1) A function z=f(x,y) defines a surface, and an equation g(x,y)=0 defines a curve on the xy-plane.
2) The points where this curve intersects the surface form a "trail".
3) The extrema on this trail occur where the gradients of the surface and constraint are parallel (or equivalently where their normals are parallel), allowing the use of Lagrange multipliers to solve the constrained optimization problem.
Relations & functions.pps
The document discusses Cartesian products, domains, ranges, and co-domains of relations and functions through examples and definitions. It explains that the Cartesian product of sets A and B, written as A×B, is the set of all ordered pairs (a,b) where a is an element of A and b is an element of B. It also defines what constitutes a relation between two sets and provides examples of relations and functions, discussing their domains and ranges. Arrow diagrams are presented to illustrate various functions along with questions and their solutions related to relations and functions.
4 areas in polar coordinates
The document discusses calculating the area swept out by a polar function r=f(θ) between the angles θ=a and θ=b. The polar area formula is given as A = (1/2) ∫f(θ)2 dθ. Formulas are derived to integrate the squares of sine and cosine in terms of the cosine double angle. These integrals are summarized. An example problem finds the area swept by r=2sin(θ) between 0 and 2π, which is 2π, the area of a circle with radius 1 swept out twice.
Functions limits and continuity
This document discusses functions, limits, and continuity. It begins by defining functions, domains, ranges, and some standard real functions like constant, identity, modulus, and greatest integer functions. It then covers limits of functions including one-sided limits and properties of limits. Examples are provided to illustrate evaluating limits using substitution and factorization methods. The overall objectives are to understand functions, domains, ranges, limits of functions and methods to evaluate limits.
Increasing and decreasing functions ap calc sec 3.3
The document discusses increasing and decreasing functions and the first derivative test. It defines that a function is increasing if the derivative is positive, decreasing if the derivative is negative, and constant if the derivative is zero. It provides examples of finding the intervals where a function is increasing or decreasing by identifying critical numbers and testing points in each interval. The document also summarizes the first derivative test, stating that a critical point is an extremum if the derivative changes sign there, and whether it is a maximum or minimum depends on if the derivative changes from negative to positive or positive to negative.
topology definitions
Topology is the branch of mathematics concerned with properties that remain unchanged by deformations such as stretching or shrinking. It studies concepts like open sets, closed sets, limits, and neighborhoods. The product topology on X × Y has as its basis all sets of the form U × V, where U is open in X and V is open in Y. Projections map elements of a product space X × Y onto the first or second factor. The subspace topology on a subset Y of a space X contains all intersections of Y with open sets of X. The interior of a set A is the largest open set contained in A, while the closure of A is the smallest closed set containing A.
1.3 Complex Numbers
This document discusses complex numbers. It defines the imaginary unit i as the number whose square is -1. Complex numbers are expressed as a + bi, where a is the real part and bi is the imaginary part. All real number properties extend to complex numbers. Operations like addition, subtraction, multiplication, division and powers of i are demonstrated. Complex conjugates are used to simplify expressions and divide complex numbers. Examples are provided to simplify expressions and perform operations on complex numbers.
Recommended
27 power series x
I. A power series is a "polynomial" with infinitely many terms of the form P(x) = Σn=0∞ anxn.
II. The radius of convergence R determines the values of x where the power series converges or diverges: it converges absolutely for |x| < R, diverges for |x| > R, and may converge or diverge at x = ±R.
III. The ratio test and root test can be used to calculate the radius of convergence R.
21 lagrange multipliers
The document describes Lagrange multipliers, which are used to find the extrema (maximum and minimum points) of a function subject to a constraint. Specifically:
1) A function z=f(x,y) defines a surface, and an equation g(x,y)=0 defines a curve on the xy-plane.
2) The points where this curve intersects the surface form a "trail".
3) The extrema on this trail occur where the gradients of the surface and constraint are parallel (or equivalently where their normals are parallel), allowing the use of Lagrange multipliers to solve the constrained optimization problem.
Relations & functions.pps
The document discusses Cartesian products, domains, ranges, and co-domains of relations and functions through examples and definitions. It explains that the Cartesian product of sets A and B, written as A×B, is the set of all ordered pairs (a,b) where a is an element of A and b is an element of B. It also defines what constitutes a relation between two sets and provides examples of relations and functions, discussing their domains and ranges. Arrow diagrams are presented to illustrate various functions along with questions and their solutions related to relations and functions.
4 areas in polar coordinates
The document discusses calculating the area swept out by a polar function r=f(θ) between the angles θ=a and θ=b. The polar area formula is given as A = (1/2) ∫f(θ)2 dθ. Formulas are derived to integrate the squares of sine and cosine in terms of the cosine double angle. These integrals are summarized. An example problem finds the area swept by r=2sin(θ) between 0 and 2π, which is 2π, the area of a circle with radius 1 swept out twice.
Functions limits and continuity
This document discusses functions, limits, and continuity. It begins by defining functions, domains, ranges, and some standard real functions like constant, identity, modulus, and greatest integer functions. It then covers limits of functions including one-sided limits and properties of limits. Examples are provided to illustrate evaluating limits using substitution and factorization methods. The overall objectives are to understand functions, domains, ranges, limits of functions and methods to evaluate limits.
Increasing and decreasing functions ap calc sec 3.3
The document discusses increasing and decreasing functions and the first derivative test. It defines that a function is increasing if the derivative is positive, decreasing if the derivative is negative, and constant if the derivative is zero. It provides examples of finding the intervals where a function is increasing or decreasing by identifying critical numbers and testing points in each interval. The document also summarizes the first derivative test, stating that a critical point is an extremum if the derivative changes sign there, and whether it is a maximum or minimum depends on if the derivative changes from negative to positive or positive to negative.
topology definitions
Topology is the branch of mathematics concerned with properties that remain unchanged by deformations such as stretching or shrinking. It studies concepts like open sets, closed sets, limits, and neighborhoods. The product topology on X × Y has as its basis all sets of the form U × V, where U is open in X and V is open in Y. Projections map elements of a product space X × Y onto the first or second factor. The subspace topology on a subset Y of a space X contains all intersections of Y with open sets of X. The interior of a set A is the largest open set contained in A, while the closure of A is the smallest closed set containing A.
1.3 Complex Numbers
This document discusses complex numbers. It defines the imaginary unit i as the number whose square is -1. Complex numbers are expressed as a + bi, where a is the real part and bi is the imaginary part. All real number properties extend to complex numbers. Operations like addition, subtraction, multiplication, division and powers of i are demonstrated. Complex conjugates are used to simplify expressions and divide complex numbers. Examples are provided to simplify expressions and perform operations on complex numbers.
Function and Its Types.
In detail and In very simple method That can any one understand.
If you read this all you doubts about function will be clear.
because i have used very simple example and simple English words that you can pick quickly concept about functions.
#inshallah.
Lesson 19: Maximum and Minimum Values
The closed interval method tells us how to find the extreme values of a continuous function defined on a closed, bounded interval: we check the end points and the critical points.
L19 increasing & decreasing functions
This document discusses analysis of functions including derivatives, extrema, and graphing. It defines key concepts such as increasing and decreasing functions, concavity, points of inflection, stationary points, and relative maxima and minima. It presents Rolle's theorem and the mean value theorem. Examples demonstrate finding critical points and determining the behavior of functions based on the signs of the first and second derivatives. The first and second derivative tests are introduced to identify relative extrema at critical points.
25 the ratio, root, and ratio comparison test x
The document discusses two tests for determining if an infinite series converges or diverges: the ratio test and the root test. The ratio test checks if the limit of the ratio of successive terms is less than 1, equal to 1, or greater than 1, indicating convergence, inconclusive result, or divergence, respectively. The root test checks if the limit of the nth root of terms is less than, equal to, or greater than 1, with similar implications for convergence or divergence. Examples are provided to demonstrate how to apply each test. It is also noted that if a series cannot be directly tested, an equivalent surrogate series may be used instead.
Polynomials by nikund
This ppt will help you knowing more about different types of polynomials and will help you to understand better.
rupali real analysis ppt.ppt
This document provides a summary of key concepts in real analysis related to continuous functions. It defines continuity at a point and continuity on a set. It presents theorems showing that continuity is preserved under algebraic operations, topological characterizations of continuity involving open sets, and the intermediate value theorem. It also discusses the relationship between continuity and compactness, including that a function is continuous on a compact set.
29 conservative fields potential functions
The document discusses conservative vector fields and potential functions. It defines a conservative field as one that is the gradient of a "nice" function, where the mixed partial derivatives are equal. A theorem is presented stating that a vector field F is conservative if and only if its partial derivatives satisfy fy = gx. An example shows a given vector field is conservative by verifying this condition. The potential function for the example field is then found by partial integration.
Integral (area)
The document discusses using definite integrals to find the area under a curve. It provides examples of finding the area of various shaded regions bounded by curves and the x-axis using the formula: area = ∫f(x)dx from x=a to x=b. It also shows how to find the coordinates of points where two curves intersect in order to divide the region into multiple areas and calculate them separately.
Independence, basis and dimension
This document discusses linear independence, basis, and dimension in linear algebra. It defines linear independence as vectors being linearly independent if the only solution that produces the zero vector is the trivial solution with all coefficients equal to zero. A basis is defined as a set of linearly independent vectors that span the vector space. The dimension of a vector space is the number of vectors in any basis of that space. The dimensions of the four fundamental subspaces (row space, column space, nullspace, and left nullspace) of a matrix are defined in terms of the rank of the matrix.
Ring
These Slides Consists of
Ring
Zero Divisor
Unit Element of Ring
Division Ring or Skew Field
Field:
Commutative Ring
Ring with unity (identity)
Relations and functions
The document discusses functions, relations, domains, ranges and using vertical line tests, mappings, tables and graphs to represent and analyze functions. It provides examples of determining if a relation is a function, finding domains and ranges, modeling function rules with tables and graphs using given domains, and solving other function problems.
Linear equation in two variables
This document discusses solving systems of linear equations in two variables. There are three main algebraic methods discussed: 1) elimination by substitution, which involves substituting one variable's expression into the other equation to get an equation with just one variable; 2) elimination by equating coefficients, which involves multiplying equations by constants and subtracting to eliminate one variable; and 3) cross-multiplication, which uses cross-multiplication of fractions to eliminate one variable. An example of using elimination by substitution to solve the system x + 2y = -1 and 2x - 3y = 12 is shown.
Real analysis
This document provides an overview of topics in real analysis including countable and uncountable sets, open and closed sets, connected sets, and limit points. It defines bounded and unbounded sets, with an unbounded set not being of finite size. Open sets are defined as sets containing all their limit points, while closed sets can be approximated in a metric space by containing limit points. Limit points are also defined as points that can be approximated by other points in a set's neighborhood excluding the point itself. Images are provided as examples of open and closed sets.
Introduction to Groups and Permutation Groups
Basic concept of Groups and a detailed understanding of Permutation Groups with examples and solved questions.
Limits in Maths presentation
The document defines limits and properties of limits in mathematics. It presents limits to Sir Nasir Nadeem on behalf of several students. Limits are defined as the value a function approaches as the input approaches some value and are essential to calculus. The properties of limits include the sum rule, difference rule, product rule, quotient rule, and constant rule. One-sided limits and techniques for calculating limits such as direct substitution, rationalization, and limits at infinity are also described.
Cartesian product of two sets
This material will useful for school level students .
If you want to download this material, Please send me a mail or comment
Lesson 26: Integration by Substitution (slides)
The document provides an example of using the substitution method to evaluate the indefinite integral ∫(x2 + 3)3 4x dx. It introduces the substitution u = x2 + 3, which allows the integral to be rewritten as ∫u3 2 du and then evaluated as (1/2)u4 = (1/2)(x2 + 3)4. The solution is compared to directly integrating the expanded polynomial. The document outlines the theory and notation of substitution for indefinite integrals.
Analytic function
Analytic Function, C-R equation, Harmonic function, laplace equation, Construction of analytic function, Critical point, Invariant point , Bilinear Transformation
4.3 related rates
The document discusses related rates problems. It begins by using resizing a rectangle on a computer screen as an example to demonstrate how the rates of change of the length (L) and width (W) relate to the rate of change of the area (A). The key steps are: (1) the area A is given by A=LW, (2) take the derivative of both sides, (3) use the product rule and chain rule to obtain A'=L'W+LW', (4) plug in the given rates of L' and W' to solve for A'.
The document then provides examples to demonstrate how to set up and solve related rates problems by translating the given rates into derivatives, applying
26 alternating series and conditional convergence x
The document discusses alternating series and conditional convergence. An alternating series has terms that alternate between positive and negative. An alternating series converges conditionally if the absolute value of its terms sums to infinity, and converges absolutely if the absolute value sums converges. Common examples like the alternating harmonic series converge conditionally. When determining if an alternating series converges, it is important to specify if it converges absolutely or conditionally.
Comuter graphics dda algorithm
DDA algorithm examples, solved examples, computer graphics, pixel calculation, line drawing algorithm, line drawing solved, 2D line drawing calculation, extra examples on DDA algorithm, Hearn and Baker book on computer graphics
Stationary points
This document discusses stationary points (SPs) and how to identify and classify them. It explains that SPs occur when the derivative of a function is equal to 0. It provides examples of finding SPs by taking the derivative, setting it equal to 0, and solving for x. It also introduces the concept of using a nature table to determine whether a SP is a maximum or minimum turning point by examining the sign of the derivative just before and after the SP. The document demonstrates this process on several examples, finding the SPs and using the nature table to classify them.
More Related Content
What's hot
Function and Its Types.
In detail and In very simple method That can any one understand.
If you read this all you doubts about function will be clear.
because i have used very simple example and simple English words that you can pick quickly concept about functions.
#inshallah.
Lesson 19: Maximum and Minimum Values
The closed interval method tells us how to find the extreme values of a continuous function defined on a closed, bounded interval: we check the end points and the critical points.
L19 increasing & decreasing functions
This document discusses analysis of functions including derivatives, extrema, and graphing. It defines key concepts such as increasing and decreasing functions, concavity, points of inflection, stationary points, and relative maxima and minima. It presents Rolle's theorem and the mean value theorem. Examples demonstrate finding critical points and determining the behavior of functions based on the signs of the first and second derivatives. The first and second derivative tests are introduced to identify relative extrema at critical points.
25 the ratio, root, and ratio comparison test x
The document discusses two tests for determining if an infinite series converges or diverges: the ratio test and the root test. The ratio test checks if the limit of the ratio of successive terms is less than 1, equal to 1, or greater than 1, indicating convergence, inconclusive result, or divergence, respectively. The root test checks if the limit of the nth root of terms is less than, equal to, or greater than 1, with similar implications for convergence or divergence. Examples are provided to demonstrate how to apply each test. It is also noted that if a series cannot be directly tested, an equivalent surrogate series may be used instead.
Polynomials by nikund
This ppt will help you knowing more about different types of polynomials and will help you to understand better.
rupali real analysis ppt.ppt
This document provides a summary of key concepts in real analysis related to continuous functions. It defines continuity at a point and continuity on a set. It presents theorems showing that continuity is preserved under algebraic operations, topological characterizations of continuity involving open sets, and the intermediate value theorem. It also discusses the relationship between continuity and compactness, including that a function is continuous on a compact set.
29 conservative fields potential functions
The document discusses conservative vector fields and potential functions. It defines a conservative field as one that is the gradient of a "nice" function, where the mixed partial derivatives are equal. A theorem is presented stating that a vector field F is conservative if and only if its partial derivatives satisfy fy = gx. An example shows a given vector field is conservative by verifying this condition. The potential function for the example field is then found by partial integration.
Integral (area)
The document discusses using definite integrals to find the area under a curve. It provides examples of finding the area of various shaded regions bounded by curves and the x-axis using the formula: area = ∫f(x)dx from x=a to x=b. It also shows how to find the coordinates of points where two curves intersect in order to divide the region into multiple areas and calculate them separately.
Independence, basis and dimension
This document discusses linear independence, basis, and dimension in linear algebra. It defines linear independence as vectors being linearly independent if the only solution that produces the zero vector is the trivial solution with all coefficients equal to zero. A basis is defined as a set of linearly independent vectors that span the vector space. The dimension of a vector space is the number of vectors in any basis of that space. The dimensions of the four fundamental subspaces (row space, column space, nullspace, and left nullspace) of a matrix are defined in terms of the rank of the matrix.
Ring
These Slides Consists of
Ring
Zero Divisor
Unit Element of Ring
Division Ring or Skew Field
Field:
Commutative Ring
Ring with unity (identity)
Relations and functions
The document discusses functions, relations, domains, ranges and using vertical line tests, mappings, tables and graphs to represent and analyze functions. It provides examples of determining if a relation is a function, finding domains and ranges, modeling function rules with tables and graphs using given domains, and solving other function problems.
Linear equation in two variables
This document discusses solving systems of linear equations in two variables. There are three main algebraic methods discussed: 1) elimination by substitution, which involves substituting one variable's expression into the other equation to get an equation with just one variable; 2) elimination by equating coefficients, which involves multiplying equations by constants and subtracting to eliminate one variable; and 3) cross-multiplication, which uses cross-multiplication of fractions to eliminate one variable. An example of using elimination by substitution to solve the system x + 2y = -1 and 2x - 3y = 12 is shown.
Real analysis
This document provides an overview of topics in real analysis including countable and uncountable sets, open and closed sets, connected sets, and limit points. It defines bounded and unbounded sets, with an unbounded set not being of finite size. Open sets are defined as sets containing all their limit points, while closed sets can be approximated in a metric space by containing limit points. Limit points are also defined as points that can be approximated by other points in a set's neighborhood excluding the point itself. Images are provided as examples of open and closed sets.
Introduction to Groups and Permutation Groups
Basic concept of Groups and a detailed understanding of Permutation Groups with examples and solved questions.
Limits in Maths presentation
The document defines limits and properties of limits in mathematics. It presents limits to Sir Nasir Nadeem on behalf of several students. Limits are defined as the value a function approaches as the input approaches some value and are essential to calculus. The properties of limits include the sum rule, difference rule, product rule, quotient rule, and constant rule. One-sided limits and techniques for calculating limits such as direct substitution, rationalization, and limits at infinity are also described.
Cartesian product of two sets
This material will useful for school level students .
If you want to download this material, Please send me a mail or comment
Lesson 26: Integration by Substitution (slides)
The document provides an example of using the substitution method to evaluate the indefinite integral ∫(x2 + 3)3 4x dx. It introduces the substitution u = x2 + 3, which allows the integral to be rewritten as ∫u3 2 du and then evaluated as (1/2)u4 = (1/2)(x2 + 3)4. The solution is compared to directly integrating the expanded polynomial. The document outlines the theory and notation of substitution for indefinite integrals.
Analytic function
Analytic Function, C-R equation, Harmonic function, laplace equation, Construction of analytic function, Critical point, Invariant point , Bilinear Transformation
4.3 related rates
The document discusses related rates problems. It begins by using resizing a rectangle on a computer screen as an example to demonstrate how the rates of change of the length (L) and width (W) relate to the rate of change of the area (A). The key steps are: (1) the area A is given by A=LW, (2) take the derivative of both sides, (3) use the product rule and chain rule to obtain A'=L'W+LW', (4) plug in the given rates of L' and W' to solve for A'.
The document then provides examples to demonstrate how to set up and solve related rates problems by translating the given rates into derivatives, applying
26 alternating series and conditional convergence x
The document discusses alternating series and conditional convergence. An alternating series has terms that alternate between positive and negative. An alternating series converges conditionally if the absolute value of its terms sums to infinity, and converges absolutely if the absolute value sums converges. Common examples like the alternating harmonic series converge conditionally. When determining if an alternating series converges, it is important to specify if it converges absolutely or conditionally.
What's hot (20)
26 alternating series and conditional convergence x
26 alternating series and conditional convergence x
Similar to Increasing decreasing functions
Comuter graphics dda algorithm
DDA algorithm examples, solved examples, computer graphics, pixel calculation, line drawing algorithm, line drawing solved, 2D line drawing calculation, extra examples on DDA algorithm, Hearn and Baker book on computer graphics
Stationary points
This document discusses stationary points (SPs) and how to identify and classify them. It explains that SPs occur when the derivative of a function is equal to 0. It provides examples of finding SPs by taking the derivative, setting it equal to 0, and solving for x. It also introduces the concept of using a nature table to determine whether a SP is a maximum or minimum turning point by examining the sign of the derivative just before and after the SP. The document demonstrates this process on several examples, finding the SPs and using the nature table to classify them.
Curve sketching
This document discusses how to sketch the graph of a function by:
1) Finding the stationary points (SPs) where the derivative is equal to 0
2) Determining where the graph intersects the x-axis and y-axis
3) Identifying the dominant term for large positive and negative values of x to understand how the graph behaves as x approaches infinity
3. DERIVATIVE BY INCREMENT IN CALULUS 01
The document discusses the concept of derivatives in calculus. It defines a derivative as the limit of the ratio of change in y over change in x as the change in x approaches zero. This represents the instantaneous rate of change of a function with respect to its variable. The document provides examples of finding the derivatives of various functions by applying this definition and using algebraic manipulation of limits. It also explains how derivatives can be used to find the slope of a curve and solve problems involving rates of change.
Closed intervals
1) The document discusses finding the maximum and minimum values of functions over closed intervals. It defines a closed interval as having limits on the domain, with maximums and minimums occurring at stationary points or end points.
2) It provides an example of finding the maximum and minimum values of the function y = 1/3x^3 - 9x over the closed interval [-4, 9]. It finds the stationary points, calculates the y-values at those points and the end points, and determines that the maximum value is 216 at x=9 and the minimum value is -18 at x=3.
3) It then provides a key question example of finding the maximum and minimum values of the function y
Calculus 08 techniques_of_integration
Trigonometric substitutions can help evaluate integrals involving trigonometric functions. The document provides examples of using trigonometric substitutions to evaluate integrals of powers of sine and cosine functions. Specifically:
1) Integrals of powers of sine and cosine can be evaluated by rewriting the functions using trigonometric identities and then substituting variables. For example, sin5x can be rewritten as sinx(sin2x)2 and evaluated using the substitution u=cosx.
2) More complex integrals may require multiple steps and identities. For example, evaluating sin6x requires rewriting sin2x using an identity and then integrating four resulting terms.
3) Trigonometric substitutions allow rewriting integrals involving
Integration intro
This document introduces integration as the reverse process of differentiation. It establishes the rule that if dy/dx = axn, then the integral is y = axn+1/(n+1) + c, where c is the constant of integration. Several examples are worked out applying this rule. The document also introduces notation for integration, including the integral sign ∫ and discusses some cases where the power is not a whole number. It emphasizes that the power in the integral must be positive.
Differentiation
The document discusses differentiation and its history. It was independently developed in the 17th century by Isaac Newton and Gottfried Leibniz. Differentiation allows the calculation of instantaneous rates of change and is used in many areas including mathematics, physics, engineering and more. Key concepts covered include calculating speed, estimating instantaneous rates of change, the rules for differentiation, and differentiation of expressions with multiple terms.
monotonicity thoery & solved & execise Module-4.pdf
In this chapter, we shall study the nature of a
function which is governed by the sign of its derivative. If the graph of a function is in upward going direction or in downward coming direction then it is called as monotonic function, and this property of the function is called Monotonicity. If a function is defined in any interval, and if in some part of the interval, graph moves upwards
A function is said to be monotonic function in a domain if it is either monotonic increasing or monotonic decreasing in that domain.
NOTE : If x < x f(x ) < f(x ) x , x D, then
and in the remaining part moves downward then
1 2 1
2 1 2
function is not monotonic in that interval.
f(x) is called strictly increasing in domain D.
These are of two types –
2.1 Monotonic Increasing :
A function f(x) defined in a domain D is said to be monotonic increasing function if the value of f(x) does not decrease (increase) by increasing (decreasing) the value of x or
We can say that the value of f(x) should increase (decrease) or remain equal by increasing
(Decreasing) the value of x.
Similarly if x1 < x2 f(x1) > f(x2), x1, x2 D then it is called strictly decreasing in domain D.
R
If Tor x1 x2 f(x1) f(x2 )
, x1 , x2 D
or SR x1 x2 f(x1) f(x2 ) , x1 , x2 D
2.2 Monotonic Decreasing :
A function f(x) defined in a domain D is said to be monotonic decreasing function if the value of f(x) does not increase (decrease) by increasing (decreasing) the value of x or
We can say that the value of f(x) should decrease (increase) or remain equal by increasing
(Decreasing) the value of x.
For Example
(i) f(x) = ex is a monotonic increasing function where as g(x) = 1/x is monotonic decreasing function.
(ii) f(x) = x2 and g(x) = | x | are monotonic increasing for x > 0 and monotonic decreasing for x < 0. In general they are not monotonic functions.
(iii) Sin x, cos x are not monotonic function whereas tan x, cot x are monotonic.
(i) At a Point : A function f(x) is said to be monotonic increasing (decreasing) at a point x = a of its domain if it is monotonic increasing
R
If Tor x1 x2 f(x1) f(x2 )
, x1 , x2 D
(decreasing) in the interval (a – h, a + h) where h is a small positive number. Hence we may
or SR x1 x2 f(x1) f(x2 ) , x1 , x2 D
observe that if f(x) is monotonic increasing at x = a, then at this point tangent to its graph will make an acute angle with the x–axis where as if the function is monotonic decreasing these tangent will make
an obtuse angle with x–axis. Consequently f' (a) will be positive or negative according as f(x) is monotonic increasing or decreasing at x = a.
Ex. Function f(x) = x2 + 1 is monotonically decreasing in [ –1, 0] because
f' (x) = 2x < 0, x (–1, 0)
Ex. Function f(x) = x2 is not a monotonic function in the interval [–1, 1] because
f' (x) > 0, when x = 1/2
Ex. Function f(x) = sin2x + cos2x is constant
Application of derivatives 2 maxima and minima
This document discusses key concepts related to derivatives and their applications:
- It defines increasing and decreasing functions and explains how to determine if a function is increasing or decreasing based on the sign of the derivative.
- It introduces the use of derivatives to find maximum and minimum values, extreme points, and critical points of functions.
- Theorems 1 and 2 provide rules for determining if a critical point represents a maximum or minimum.
- Examples are provided to demonstrate finding the intervals where a function is increasing/decreasing, identifying extrema, and determining the greatest and least function values over an interval.
Anti derivatives
The document provides examples of derivatives and their corresponding anti-derivatives (indefinite integrals) for various functions. It also demonstrates rules for taking the anti-derivative of functions using u-substitution. Some key rules covered include adding +c to account for constants and applying power rules for integrals involving terms like 4x, 3x^2, or other polynomial functions. Examples are worked through step-by-step to illustrate properly applying u-substitution and integrating more complex expressions.
CalculusStudyGuide
The document provides examples and explanations of concepts related to calculus including continuity, differentiability, limits, derivatives, and the mean value theorem. Some key points:
- It gives examples of determining if functions are continuous and differentiable at various points, including functions with absolute value.
- The mean value theorem is explained and examples are worked through showing a function satisfies the mean value theorem and finding the value of c.
- Numerous examples demonstrate calculating derivatives using rules like product, quotient, chain and implicit differentiation. Examples include derivatives of trigonometric, exponential and logarithmic functions.
- Implicit differentiation is used to find the equation of a tangent line to a curve at a given point.
INTEGRATION
This document discusses various topics related to integration including:
1. The anti-derivative and how it is the reverse of differentiation.
2. Indefinite integrals which do not have limits and require an arbitrary constant.
3. Definite integrals which do have limits and are used to find the area under a curve between two points.
4. Applications of integration such as using definite integrals to find the area under a curve or revolving an area about an axis to find the volume of a solid.
Comuter graphics bresenhams line drawing algorithm
bresenhams line drawing algorithm examples, solved examples, computer graphics, pixel calculation, hearn and baker text book on computer graphics, extra solved examples on bresenhams line drawing algorithm,
Polynomial math
1) The document discusses various methods for manipulating and solving algebraic expressions, including adding, subtracting, and factoring polynomials.
2) Factoring techniques include grouping like terms, using the difference of squares formula, and recognizing perfect square trinomials.
3) The quadratic formula is introduced as a way to solve quadratic equations of the form ax2 + bx + c = 0.
Literal Equations Wed. 9/9 notes
1) The document provides steps for solving various literal equations (formulas) for a specified variable. It gives examples of solving equations of the form 2x - 4y = 7, 2x - 4y = 7, y + a/3 = c, 4x - 2y = 12, and formulas for the volume of a rectangular prism and pyramid, for the specified variables x, y, a, h, and L. The objective is for students to learn how to isolate variables in equations by using inverse operations such as addition, subtraction, multiplication, and division.
Area between curves
The document provides steps to calculate the area between two curves by finding the intersection points using "y=y" and then integrating between those points. It works through multiple examples of finding the area between various curve combinations, including quadratic, cubic, and linear functions. The key steps are finding the intersection points using "y=y", setting up the integral as the top curve minus the bottom curve, and integrating between the bounds found from the intersection points.
Simultaneous equations
The document discusses methods for solving simultaneous linear equations, including elimination and substitution.
It provides examples of using elimination by adding or subtracting equations to remove a variable, and substitution by making one variable the subject of an equation and substituting it into the other equation. Fractions are converted to simple linear equations by finding a common denominator. The document also covers solving simultaneous equations when one equation is quadratic using substitution after making one variable the subject of the linear equation.
Similar to Increasing decreasing functions (19)
monotonicity thoery & solved & execise Module-4.pdf
monotonicity thoery & solved & execise Module-4.pdf
Comuter graphics bresenhams line drawing algorithm
Comuter graphics bresenhams line drawing algorithm
More from Shaun Wilson
Troubleshooting Computing Problems
Six steps of troubleshooting include identifying the problem, establishing a theory of probable cause, testing the theory, establishing and implementing a solution plan, verifying full system functionality, and documenting findings, actions, and outcomes. Effective troubleshooting uses a combination of open and closed questions, and thorough documentation of all investigation steps, tests, solutions, and outcomes is critical. Experienced technicians may use a half-split self-evaluation approach that combines top-down and bottom-up methods with educated guesses to efficiently diagnose and resolve issues.
Professionalism and Ethics
This document discusses several topics related to professionalism and ethics in computing including professional bodies, codes of conduct, and key UK legislation around data protection, computer misuse, equality, health and safety, waste disposal, and intellectual property. Professional bodies provide certifications and resources for members, set technical standards, and bring professionals together. Codes of conduct require professionals to act with integrity, reject bribery, uphold their profession's reputation, and protect confidential information. Legislation discussed governs data protection, computer security, equality in the workplace, health and safety, proper waste disposal, and copyright.
Software Development (Mobile Technology)
This document discusses key concepts in software development including data types like boolean, integer, real, and string. It also covers programming constructs such as sequence, selection, and iteration. Finally, it outlines the typical documentation for a software project like requirements specification, test plans, code listings, and completed test logs.
Computer Systems Fundamentals
This document provides an overview of computer systems fundamentals including logic gates, number conversions, layers of the operating system, and components of a basic computer system. Specifically, it discusses:
1. Logic gates like AND, OR, and NOT and their truth tables.
2. Conversions between number bases like binary, decimal, and hexadecimal with examples.
3. The main layers of an operating system including the user interface, file management, input/output, memory management, and kernel.
4. Key components of a computer system including the ALU, control unit, registers, buses, and ASCII character encoding.
Introduction to Project Management Assessment Notes
This document provides an introduction and overview of key project management concepts. It defines what a project is, including that projects have unique goals, defined timelines and budgets. It discusses project tasks, stakeholders, and tools like work breakdown structures, Gantt charts, PERT charts and scope management. PERT charts in particular help schedule projects and identify the critical path of tasks. Careful scope and change management is important to avoid feature creep from altering the original project plan.
SQL Assessment Command Statements
The document provides examples and explanations of common SQL commands used to query, manipulate, and manage data in a relational database. Key points include:
- The SELECT statement is used to query data from database tables. The WHERE clause filters results.
- INSERT, UPDATE and DELETE statements are used to add, modify and remove rows in database tables.
- CREATE, ALTER, DROP statements manage the database schema by creating, modifying and deleting tables, columns, keys and constraints.
- PRIMARY KEY and FOREIGN KEY constraints enforce data integrity and relationships between tables.
The Rise and Fall of the Roman Empire
The document provides an overview of the rise and fall of the Roman Empire from 509 BCE to 476 CE. It discusses the transition from Roman Republic to Roman Empire under Augustus, key emperors like Tiberius, Caligula, Nero, Vespasian, and Hadrian, as well as the division of the empire into eastern and western halves under Diocletian. It also examines factors that contributed to the decline of the western empire, including invasions by barbarian tribes and the removal of the capital to Constantinople, while the eastern empire continued on as the Byzantine Empire until 1453.
National 5 Graphic Communication
The document discusses color theory and desktop publishing principles. It describes primary, secondary and tertiary colors. It also discusses tints, shades, warm and cold colors. It outlines design principles like alignment, bleed, captions and drop caps. It provides information on fonts, headers, footers, guides and page layout features.
Vector journeys!
The document discusses vectors and their components. It provides examples of finding the components of vectors using other known vectors, such as finding the components of vector AC given the components of vectors AB and BC. It also discusses using the triangle rule to find unknown vectors. Diagrams are included to illustrate different vector problems and solutions.
Vector multiplication dot product
The document discusses vector multiplication using the dot product. It provides two formulas for calculating the dot product:
1) a.b = |a| |b| cosθ, where |a| and |b| are the magnitudes of the vectors, θ is the angle between them, and cosθ gives the effectiveness of their interaction. The dot product is largest when the vectors are parallel (θ = 0).
2) For vectors in 3D space, a.b = x1x2 + y1y2 + z1z2, where the x, y, z components of each vector are multiplied and summed.
It provides examples of calculating the dot product using both formulas in different vector
Dot product calc angle to finish!
This document discusses using the dot product to calculate the angle between two vectors. It provides the formula for calculating the dot product and shows examples of using the formula to find the angle between vectors. It also discusses how if two vectors are perpendicular, their dot product will equal 0.
Unit vectors 14
This document introduces unit vectors and how they can be used to write the components of a vector. It defines a unit vector as having a magnitude of 1 and lists the standard unit vectors i, j, k. It then shows how any vector can be written as the sum of its components in the direction of each unit vector, using examples like 3i + 4j + 7k. Finally, it provides additional examples of writing vectors in component form using unit vectors and calculating the sum of two vectors.
Vector bits and pieces
This document provides information about vectors, including:
- The relationship between the magnitude of a vector and the cosine of the angle between two vectors in determining their dot product.
- Unit vectors have a magnitude of 1 and are perpendicular to each other.
- Examples are given of calculating the dot product of vectors in different geometric configurations by decomposing into the dot products of the vectors with the unit vectors.
- Key steps are to start from the same point when calculating dot products of vectors in a figure.
Vectors intro
Vectors can represent journeys with distance and direction. They have components that work like coordinates and magnitude that is calculated using Pythagoras. Vectors can be added by placing them nose to tail and adding corresponding components, subtracted by adding the negative vector, and multiplied by a scalar by multiplying each component.
Ratios
The document discusses applying ratios to vectors. It provides examples of using ratios to find unknown points along vectors. The key steps are: 1) Form an equation using the position vector rule relating the unknown point P to the known endpoints A and B; 2) Make P the subject of the equation; 3) Solve the equation to find the coordinates of P. Examples show setting up equations for points dividing vectors in given ratios and solving to find the coordinates of the unknown points.
Parallel + collinear vectors
Vectors AB and CD are parallel if their direction vectors are proportional.
Vectors A, B, and C are collinear if their direction vectors are proportional and they share a common point.
Three examples are given to demonstrate proving vectors are parallel or collinear by showing their direction vectors are proportional.
Position and 3 d vectors amended
This document discusses position vectors in 2D and 3D coordinate systems.
- A position vector starts at the origin and represents the displacement from the origin to a point P defined by its coordinates.
- The position vector rule states that the position vector from point P to point R is equal to the vector from R's position vector subtracted by P's position vector.
- Position vectors and their properties like magnitude, addition, subtraction, and scalar multiplication follow the same rules in 3D as in 2D. Several examples are provided to demonstrate calculating the position vector and magnitude between two points in 3D space.
Solving trig equations higher
The document provides information on solving more difficult trigonometric equations. It discusses finding the acute angle and related angles, using trig function properties to isolate the angle, and considering additional solutions that occur every period of the trig function. Example problems are worked through step-by-step to demonstrate these concepts.
Solving trig equations + double angle formulae
1) The document discusses solving trigonometric equations using compound angle formulas and double angle formulas.
2) It provides examples of using these formulas to solve equations such as sin2x + cosx = 0, 2sinxcosx + cosx = 0, and cos2x - sinx = 0.
3) The key steps are to use a double angle formula to get one side equal to zero, factorize the equation, and then solve the resulting trigonometric mini equations.
Solving exponential equations
This document discusses solving exponential equations by taking the log of both sides. It shows how to solve equations with unknown powers and equations containing e as the base. The key steps are:
1) Isolate the term with the unknown power
2) Take the log of both sides
3) Use properties of logs to isolate the unknown variable
4) Calculate the value of the variable
Examples are provided to illustrate solving equations with unknown powers, equations containing e, and applying the method to context problems. The overall approach is to take logs to transform exponential equations into linear equations that can be easily solved.
More from Shaun Wilson (20)
Introduction to Project Management Assessment Notes
Introduction to Project Management Assessment Notes
Recently uploaded
THE SACRIFICE HOW PRO-PALESTINE PROTESTS STUDENTS ARE SACRIFICING TO CHANGE T...
The recent surge in pro-Palestine student activism has prompted significant responses from universities, ranging from negotiations and divestment commitments to increased transparency about investments in companies supporting the war on Gaza. This activism has led to the cessation of student encampments but also highlighted the substantial sacrifices made by students, including academic disruptions and personal risks. The primary drivers of these protests are poor university administration, lack of transparency, and inadequate communication between officials and students. This study examines the profound emotional, psychological, and professional impacts on students engaged in pro-Palestine protests, focusing on Generation Z's (Gen-Z) activism dynamics. This paper explores the significant sacrifices made by these students and even the professors supporting the pro-Palestine movement, with a focus on recent global movements. Through an in-depth analysis of printed and electronic media, the study examines the impacts of these sacrifices on the academic and personal lives of those involved. The paper highlights examples from various universities, demonstrating student activism's long-term and short-term effects, including disciplinary actions, social backlash, and career implications. The researchers also explore the broader implications of student sacrifices. The findings reveal that these sacrifices are driven by a profound commitment to justice and human rights, and are influenced by the increasing availability of information, peer interactions, and personal convictions. The study also discusses the broader implications of this activism, comparing it to historical precedents and assessing its potential to influence policy and public opinion. The emotional and psychological toll on student activists is significant, but their sense of purpose and community support mitigates some of these challenges. However, the researchers call for acknowledging the broader Impact of these sacrifices on the future global movement of FreePalestine.
A Visual Guide to 1 Samuel | A Tale of Two Hearts
These slides walk through the story of 1 Samuel. Samuel is the last judge of Israel. The people reject God and want a king. Saul is anointed as the first king, but he is not a good king. David, the shepherd boy is anointed and Saul is envious of him. David shows honor while Saul continues to self destruct.
How to Download & Install Module From the Odoo App Store in Odoo 17
Custom modules offer the flexibility to extend Odoo's capabilities, address unique requirements, and optimize workflows to align seamlessly with your organization's processes. By leveraging custom modules, businesses can unlock greater efficiency, productivity, and innovation, empowering them to stay competitive in today's dynamic market landscape. In this tutorial, we'll guide you step by step on how to easily download and install modules from the Odoo App Store.
BIOLOGY NATIONAL EXAMINATION COUNCIL (NECO) 2024 PRACTICAL MANUAL.pptx
Practical manual for National Examination Council, Nigeria.
Contains guides on answering questions on the specimens provided
Wound healing PPT
This document provides an overview of wound healing, its functions, stages, mechanisms, factors affecting it, and complications.
A wound is a break in the integrity of the skin or tissues, which may be associated with disruption of the structure and function.
Healing is the body’s response to injury in an attempt to restore normal structure and functions.
Healing can occur in two ways: Regeneration and Repair
There are 4 phases of wound healing: hemostasis, inflammation, proliferation, and remodeling. This document also describes the mechanism of wound healing. Factors that affect healing include infection, uncontrolled diabetes, poor nutrition, age, anemia, the presence of foreign bodies, etc.
Complications of wound healing like infection, hyperpigmentation of scar, contractures, and keloid formation.
HYPERTENSION - SLIDE SHARE PRESENTATION.
IT WILL BE HELPFULL FOR THE NUSING STUDENTS
IT FOCUSED ON MEDICAL MANAGEMENT AND NURSING MANAGEMENT.
HIGHLIGHTS ON HEALTH EDUCATION.
skeleton System.pdf (skeleton system wow)
🔥🔥🔥🔥🔥🔥🔥🔥🔥
إضغ بين إيديكم من أقوى الملازم التي صممتها
ملزمة تشريح الجهاز الهيكلي (نظري 3)
💀💀💀💀💀💀💀💀💀💀
تتميز هذهِ الملزمة بعِدة مُميزات :
1- مُترجمة ترجمة تُناسب جميع المستويات
2- تحتوي على 78 رسم توضيحي لكل كلمة موجودة بالملزمة (لكل كلمة !!!!)
#فهم_ماكو_درخ
3- دقة الكتابة والصور عالية جداً جداً جداً
4- هُنالك بعض المعلومات تم توضيحها بشكل تفصيلي جداً (تُعتبر لدى الطالب أو الطالبة بإنها معلومات مُبهمة ومع ذلك تم توضيح هذهِ المعلومات المُبهمة بشكل تفصيلي جداً
5- الملزمة تشرح نفسها ب نفسها بس تكلك تعال اقراني
6- تحتوي الملزمة في اول سلايد على خارطة تتضمن جميع تفرُعات معلومات الجهاز الهيكلي المذكورة في هذهِ الملزمة
واخيراً هذهِ الملزمة حلالٌ عليكم وإتمنى منكم إن تدعولي بالخير والصحة والعافية فقط
كل التوفيق زملائي وزميلاتي ، زميلكم محمد الذهبي 💊💊
🔥🔥🔥🔥🔥🔥🔥🔥🔥
Geography as a Discipline Chapter 1 __ Class 11 Geography NCERT _ Class Notes...
Geography as discipline
Elevate Your Nonprofit's Online Presence_ A Guide to Effective SEO Strategies...
Whether you're new to SEO or looking to refine your existing strategies, this webinar will provide you with actionable insights and practical tips to elevate your nonprofit's online presence.
How to Manage Reception Report in Odoo 17
A business may deal with both sales and purchases occasionally. They buy things from vendors and then sell them to their customers. Such dealings can be confusing at times. Because multiple clients may inquire about the same product at the same time, after purchasing those products, customers must be assigned to them. Odoo has a tool called Reception Report that can be used to complete this assignment. By enabling this, a reception report comes automatically after confirming a receipt, from which we can assign products to orders.
BPSC-105 important questions for june term end exam
BPSC-105 important questions for june term end exam
CapTechTalks Webinar Slides June 2024 Donovan Wright.pptx
Slides from a Capitol Technology University webinar held June 20, 2024. The webinar featured Dr. Donovan Wright, presenting on the Department of Defense Digital Transformation.
KHUSWANT SINGH.pptx ALL YOU NEED TO KNOW ABOUT KHUSHWANT SINGH
INDIA`S OWN LITERARY GENIUS MR.KHUSHWANT SINGH WAS TRULY A VERY BRAVE SOUL AND WAS AWARDED WITH THE MAGIC OF WORDS BY GOD.
Recently uploaded (20)
spot a liar (Haiqa 146).pptx Technical writhing and presentation skills
spot a liar (Haiqa 146).pptx Technical writhing and presentation skills
THE SACRIFICE HOW PRO-PALESTINE PROTESTS STUDENTS ARE SACRIFICING TO CHANGE T...
THE SACRIFICE HOW PRO-PALESTINE PROTESTS STUDENTS ARE SACRIFICING TO CHANGE T...
220711130088 Sumi Basak Virtual University EPC 3.pptx
220711130088 Sumi Basak Virtual University EPC 3.pptx
How to Download & Install Module From the Odoo App Store in Odoo 17
How to Download & Install Module From the Odoo App Store in Odoo 17
BIOLOGY NATIONAL EXAMINATION COUNCIL (NECO) 2024 PRACTICAL MANUAL.pptx
BIOLOGY NATIONAL EXAMINATION COUNCIL (NECO) 2024 PRACTICAL MANUAL.pptx
Geography as a Discipline Chapter 1 __ Class 11 Geography NCERT _ Class Notes...
Geography as a Discipline Chapter 1 __ Class 11 Geography NCERT _ Class Notes...
Elevate Your Nonprofit's Online Presence_ A Guide to Effective SEO Strategies...
Elevate Your Nonprofit's Online Presence_ A Guide to Effective SEO Strategies...
REASIGNACION 2024 UGEL CHUPACA 2024 UGEL CHUPACA.pdf
REASIGNACION 2024 UGEL CHUPACA 2024 UGEL CHUPACA.pdf
BPSC-105 important questions for june term end exam
BPSC-105 important questions for june term end exam
CapTechTalks Webinar Slides June 2024 Donovan Wright.pptx
CapTechTalks Webinar Slides June 2024 Donovan Wright.pptx
KHUSWANT SINGH.pptx ALL YOU NEED TO KNOW ABOUT KHUSHWANT SINGH
KHUSWANT SINGH.pptx ALL YOU NEED TO KNOW ABOUT KHUSHWANT SINGH
Increasing decreasing functions
- 2. What is to be learned? • What is meant by increasing/decreasing functions • How we work out when function is increasing/decreasing • How to show if a function is always increasing/decreasing
- 3. increasing increasing decreasing need to find SPs dy /dx = 0 Increasing → dy /dx is +ve Decreasing → dy /dx is -ve
- 4. Ex y = 4x3 – 3x2 + 10 Function Decreasing? For SPs dy /dx = 0 dy /dx = 12x2 – 6x 12x2 – 6x = 0 6x(2x – 1) = 0 6x = 0 or 2x – 1 = 0 x = 0 or x = ½
- 5. Nature Table y = 4x3 – 3x2 + 10 dy /dx = 12x2 – 6x = 6x(2x – 1) SPs at x = 0 and ½ x 0 dydy //dxdx = 6x(2x – 1)= 6x(2x – 1) 0 -1 ¼ = + = - Slope Max TP at x = 0 ½ 1 = + 0 Min TP at x = ½ - X - + X - + X + Decreasing 0 < x < ½
- 6. Function always increasing? • dy /dx always +ve (i.e > 0) Ex y =x3 + 7x dy /dx = 3x2 + 7 Increasing as dy /dx > 0 for all x.
- 7. Function always decreasing • dy /dx always -ve (i.e < 0) Ex y = -6x -x3 dy /dx = -6 - 3x2 Decreasing as dy /dx < 0 for all x.
- 8. Less obvious y = 1 /3x3 + 3x2 + 11x dy /dx= x2 + 6x + 11 completing square (x + 3)2 – 9 + 11 (x + 3)2 + 2 Increasing as dy /dx > 0 for all x.
- 9. Increasing/Decreasing Functions • Increasing → Gradient +ve (dy /dx > 0) • Decreasing → Gradient -ve (dy /dx < 0) • Find SPs (only need x values) • Completing square can be handy tactic
- 10. Ex y = 1 /3x3 + 4x2 + 17x dy /dx= x2 + 8x + 17 completing square (x + 4)2 – 16 + 17 (x + 4)2 + 1 Increasing as dy /dx > 0 for all x.