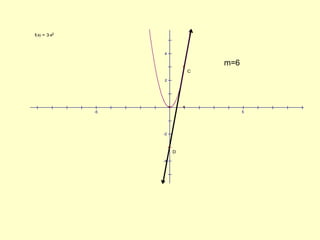
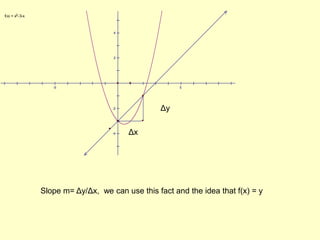
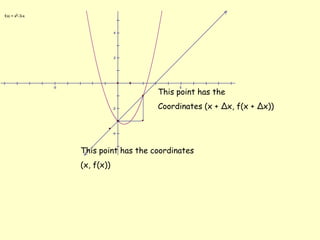
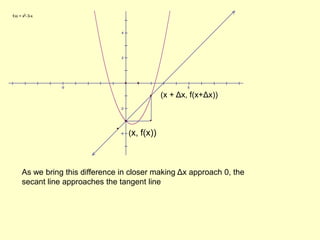
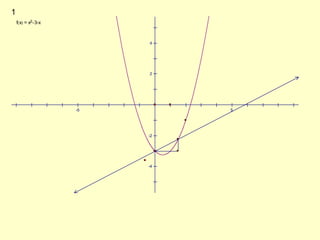
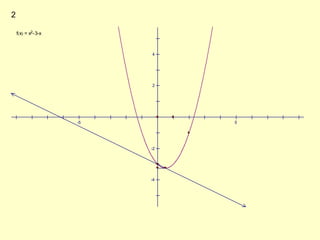
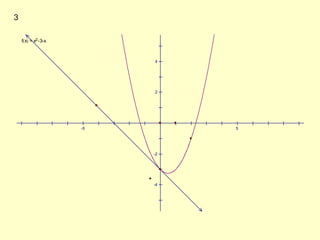
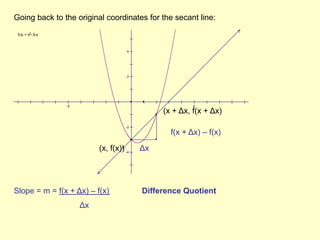
The document discusses how to identify tangent lines and find derivatives using limits. It defines the slope of a tangent line as the rate of change of a graph at a given point. To calculate slope, it uses the limit of the difference quotient as the change in x (Δx) approaches 0. This defines the derivative as the slope of the tangent line. It provides an example of finding the derivative of f(x)=x^2 at the point (2,4) using this limit process.

1. Derivatives and Slopes:Goal: identify tangent lines to a graphUse limits to find slope Use limits to find derivativesTangent Line to a Graph:The slope of the line tangent to a curve at a given point determines the rate at which the graph rises or falls at that given point.http://www.ies.co.jp/math/java/calc/index.html

2. m=6

3. Slope and limit:Just looking at the graph can be difficult and inaccurate.Secant line recall from geometry a secant is a line that passes through two points on a circle.

4. Is a secant line of circle C

5. ΔyΔxSlope m= Δy/Δx, we can use this fact and the idea that f(x) = y

6. This point has the Coordinates (x + Δx, f(x + Δx))This point has the coordinates(x, f(x))

7. (x + Δx, f(x+Δx))(x, f(x))As we bring this difference in closer making Δx approach 0, the secant line approaches the tangent line

8. 1

9. 2

10. 3

11. Going back to the original coordinates for the secant line:(x + Δx, f(x + Δx)f(x + Δx) – f(x)(x, f(x)) ΔxSlope = m = f(x + Δx) – f(x) Difference QuotientΔx

12. Definition of the Slope of a Graph:The slope m of the graph of ƒ at the point (x, ƒ(x)) is equal to the slope of its tangent line at (x, ƒ(x)), and is given by msec = m = Provided this limit exists.

13. Use the limit process to find slope. m =

14. Ex. ƒ(x)= x2 at the point (2, 4) find the slope of the graph at this point.lim ƒ(2 + Δx) – ƒ(2)Δx->0 Δx lim (2 + Δx)2 – (2)2Δx->0 Δx lim 4 + 4 Δx + Δx2 -4Δx->0 Δx

15. lim 4 Δx + Δx2Δx->0 Δx lim Δx(4 + Δx) Δx->0 Δx lim (4 + Δx) = 4Δx->0

16. Find the slope of the graph y = 2x + 5 using the limit process