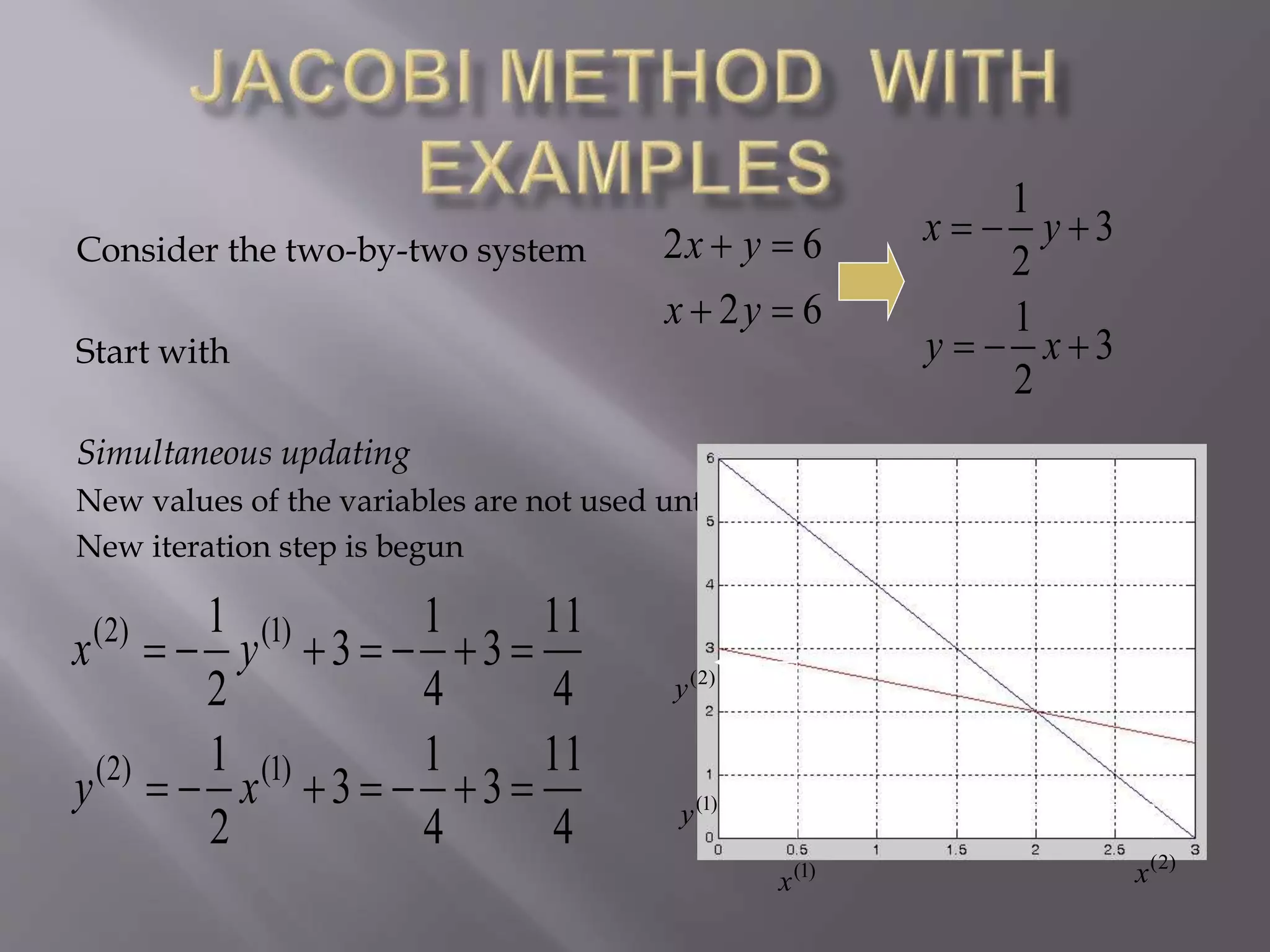
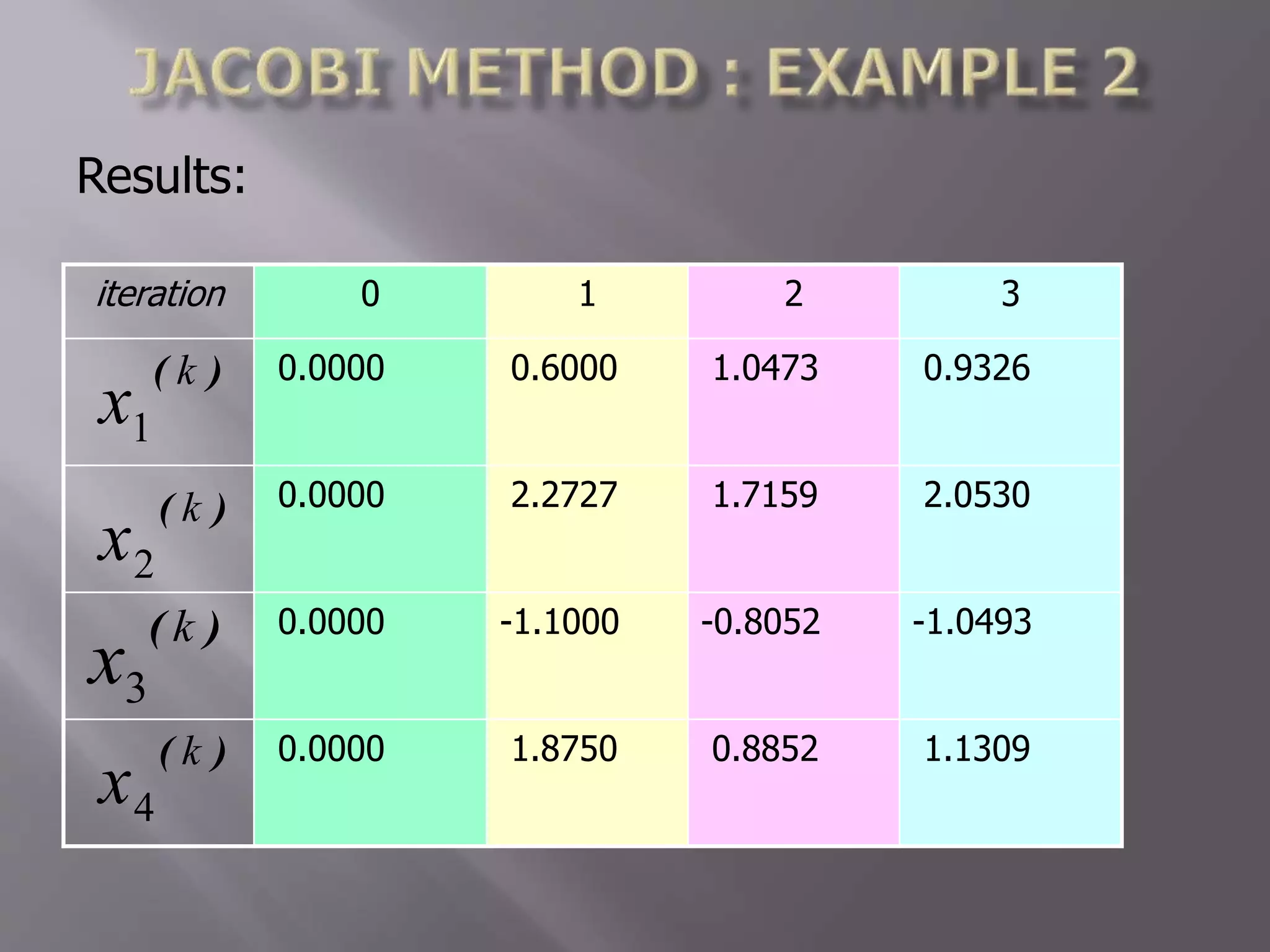
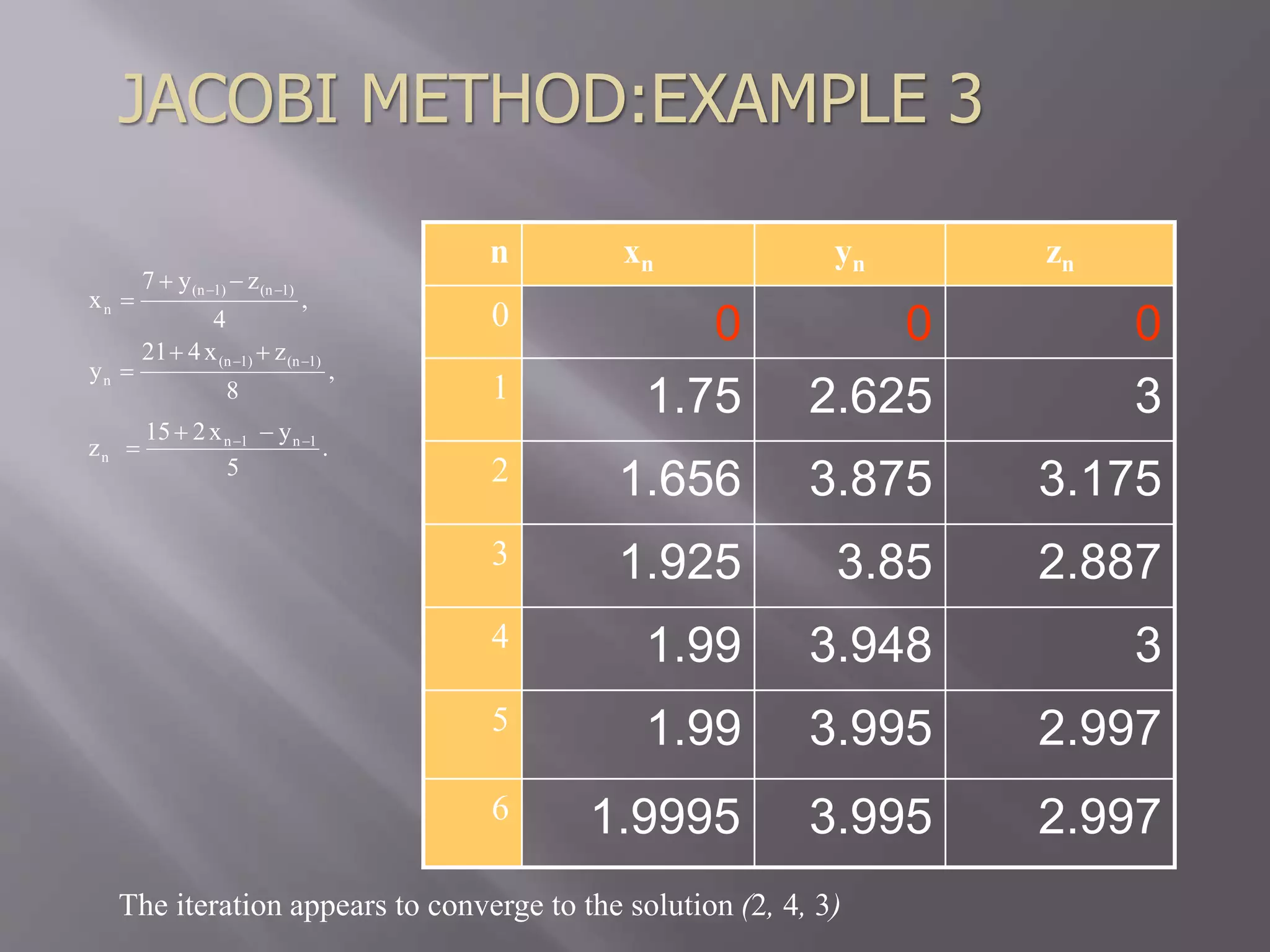
The document discusses the solution of a system of linear equations using Jacobi's method, providing detailed iterations and approximations. It includes multiple examples with starting values, iterative results, and convergence to the final solution. The text also presents programming code to implement the Jacobi method for solving the equations.

2. Convert the system:
into the equivalent system: dCxx 
3333132131
2323122121
1313212111
bxaxaxa
bxaxaxa
bxaxaxa



33
3
2
33
32
1
33
31
3
22
2
3
22
23
1
22
21
2
11
1
3
11
13
2
11
12
1
a
b
x
a
a
x
a
a
x
a
b
x
a
a
x
a
a
x
a
b
x
a
a
x
a
a
x



BAx 

3. Generate a sequence of approximation:
,..., )2()1(
xx dCxx kk
  )1()(

4. nnnnnn
nn
nn
bxaxaxa
bxaxaxa
bxaxaxa







2211
22222121
11212111















0
0
2
0
1
0
nx
x
x
x

)(
1 0
1
0
2121
11
1
1 nn xaxab
a
x  
)(
1 0
2
0
323
0
1212
22
1
2 nn xaxaxab
a
x  
)(
1 0
11
0
22
0
11
1
 nnnnnn
nn
n xaxaxab
a
x 






  

 

1
1 1
1 1 i
j
n
ij
k
jij
k
jiji
ii
k
i
xaxab
a
x

5. Consider the two-by-two system
Start with
Simultaneous updating
New values of the variables are not used until a
New iteration step is begun
4
11
3
4
1
3
2
1
4
11
3
4
1
3
2
1
)1()2(
)1()2(


xy
yx
62
62


yx
yx
3
2
1
3
2
1


xy
yx
)1(
x
)1(
y
)2(
y
)2(
x

6. Con’t
8
13
3
8
11
3
2
1
8
13
3
8
11
3
2
1
)2()3(
)2()3(


xy
yx

7. The set of equations:
020i12i5i-
2-12i-20i0i
105i-0i9i
321
321
321



Let us write for i1, i2 and i3 as
 
 
  )(.
)(
)(
3i60000i0.2500/2012ii5i
20.6000i0.1000-/2012i2-i
10.5556i1.1111/95i10i
21313
232
231



Let us make an initial guess as i1 = 0.0; i2 =0.0 and i3 = 0.0
First iteration results: i1 = 1.1111; i2 =-0.1000 and i3 = 0.0

8. First iteration results: i1 = 1.1111; i2 =-0.1000 and i3 = 0.0
Second iteration results: i1 = 1.1111; i2 =-0.1000 and i3 = 0.22
Third iteration results: i1 = 1.23; i2 = 0.03 and i3 = 0.22
Fourth iteration results: i1 = 1.23 ; i2 = 0.03 and i3 = 0.33
Fifth iteration results: i1 = 1.29; i2 = 0.1 and i3 = 0.33
Sixth iteration results: i1 = 1.29; i2 = 0.1 and i3 = 0.38
 
 
  )(.
)(
)(
3i60000i0.2500/2012ii5i
20.6000i0.1000-/2012i2-i
10.5556i1.1111/95i10i
21313
232
231




9. Consider the following set of equations.
15
11
25
6
83
102
311
210
432
4321
4321
321








xxx
xxxx
xxxx
xxx
Convert the set Ax = b in the form of x = Tx + c.
8
15
8
1
8
3
10
11
10
1
10
1
5
1
11
25
11
3
11
1
11
1
5
3
5
1
10
1
324
4213
4312
321




xxx
xxxx
xxxx
xxx

10. 8
15
8
1
8
3
10
11
10
1
10
1
5
1
11
25
11
3
11
1
11
1
5
3
5
1
10
1
)0(
3
)0(
2
)1(
4
)0(
4
)0(
2
)0(
1
)1(
3
)0(
4
)0(
3
)0(
1
)1(
2
)0(
3
)0(
2
1
1




xxx
xxxx
xxxx
xxx
)(
.0and0,0,0
)0(
4
)0(
3
)0(
2
)0(
1  xxxx
8
15
(0)
8
1
(0)
8
3
10
11
(0)
10
1
(0)
10
1
(0)
5
1
11
25
(0)
11
3
(0)
11
1
(0)
11
1
5
3
(0)
5
1
(0)
10
1
)1(
4
)1(
3
)1(
2
1
1




x
x
x
x
)(
8750.1
1000.1
,2727.2
,6000.0
)1(
4
)1(
3
)1(
2
)1(
1




x
x
x
x

11. 8
15
8
1
8
3
10
11
10
1
10
1
5
1
11
25
11
3
11
1
11
1
5
3
5
1
10
1
)1(
3
)1(
2
)2(
4
)1(
4
)1(
2
)1(
1
)2(
3
)1(
4
)1(
3
)1(
1
)2(
2
)1(
3
)1(
2
2
1




xxx
xxxx
xxxx
xxx
)(
8
15
8
1
8
3
10
11
10
1
10
1
5
1
11
25
11
3
11
1
11
1
5
3
5
1
10
1
)1(
3
)1(
2
)(
4
)1(
4
)1(
2
)1(
1
)(
3
)1(
4
)1(
3
)1(
1
)(
2
)1(
3
)1(
21








kkk
kkkk
kkkk
kk(k)
xxx
xxxx
xxxx
xxx

12. Results:
iteration 0 1 2 3
0.0000 0.6000 1.0473 0.9326
0.0000 2.2727 1.7159 2.0530
0.0000 -1.1000 -0.8052 -1.0493
0.0000 1.8750 0.8852 1.1309
)( k
x1
)( k
x2
)( k
x3
)( k
x4

13. Solve the linear system by Jacobi’s method
4x -y + z = 7
4x -8y+ z = -21
-2x + y + 5z = 15.
From the system of linear equation we get:
.
5
yx215
z
,
8
zx421
y
,
4
zy7
x
1n1n
n
1)(n1)(n
n
1)(n1)(n
n









If we start with (x0, y0, z0) = (0, 0, 0),
.
5
yx215
z
,
8
zx421
y
,
4
zy7
x








14. .
5
yx215
z
,
8
zx421
y
,
4
zy7
x
1n1n
n
1)(n1)(n
n
1)(n1)(n
n









znynxnn
0000
32.6251.751
3.1753.8751.6562
2.8873.851.9253
33.9481.994
2.9973.9951.995
2.9973.9951.99956
The iteration appears to converge to the solution (2, 4, 3)
JACOBI METHOD:EXAMPLE 3

15. 5x – 2y + 3z = -1
-3x + 9y + z =2
2x - y -7z = 3
Solve the linear system by Jacobi’s method
Continue the iterations until two successive approximations are identical
when rounded to
three significant digits.
To begin, write the system in the form
If we start with (x0, y0, z0) = (0, 0, 0),
.
7
yx23
z
,
9
zx32
y
,
5
z3y21
x







17. #include<stdio.h>
#include<conio.h>
#include<math.h>
#define ESP 0.0001
#define X1(x2,x3) ((17 - 20*(x2) + 2*(x3))/20)
#define X2(x1,x3) ((-18 - 3*(x1) + (x3))/20)
#define X3(x1,x2) ((25 - 2*(x1) + 3*(x2))/20)
void main()
{
double x1=0,x2=0,x3=0,y1,y2,y3;
int i=0;
clrscr();
printf("n__________________________________________n");
printf("n x1tt x2tt x3n");
printf("n__________________________________________n");
printf("n%ft%ft%f",x1,x2,x3);
do
{

18. y1=X1(x2,x3);
y2=X2(x1,x3);
y3=X3(x1,x2);
if(fabs(y1-x1)<ESP && fabs(y2-x2)<ESP && fabs(y3-x3)<ESP )
{
printf("n__________________________________________n");
printf("nnx1 = %.3lf",y1);
printf("nnx2 = %.3lf",y2);
printf("nnx3 = %.3lf",y3);
i = 1;
}
else
{
x1 = y1;
x2 = y2;
x3 = y3;
printf("n%ft%ft%f",x1,x2,x3);
}
}
while(i != 1);
getch();
}

19. x1 x2 x3
0.000000 0.000000 0.000000
0.850000 -0.900000 1.250000
1.875000 -0.965000 1.030000
1.918000 -1.129750 0.917750
2.071525 -1.141812 0.888737
2.080686 -1.166292 0.871576
2.103449 -1.168524 0.866988
2.105223 -1.172168 0.864376
2.108606 -1.172565 0.863653
2.108930 -1.173108 0.863255
2.109434 -1.173177 0.863141
__________________________________________
x1 = 2.109
x2 = -1.173
x3 = 0.863
Outpu
t:

20. Presented by:
Grishma Maravia