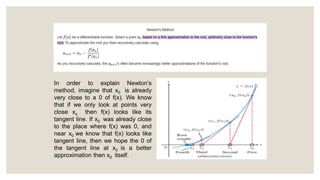
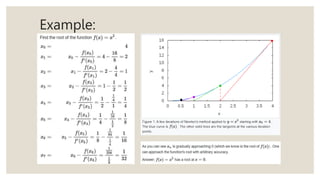
Newton's method is a recursive algorithm that uses the tangent line of a function at a given point to approximate the roots, or zeros, of that function. It starts with an initial guess and iteratively calculates better approximations of the root by taking the tangent line's x-intercept as the next guess, continuing until reaching a value close enough to the actual root. This method can find approximations of roots for any differentiable function, whether polynomial or not, as long as the function is differentiable in the desired interval.

1. NEWTON’S METHOD
Calculus

2. Newton’s Method:
◦ Newton’s method also called the Newton-Raphson method is a
recursive algorithm for approximating the root of a differentiable
function.
◦ The Newton-Raphson method is a method for approximation the roots
of polynomial equation of any order.
◦ In fact the method works for any equation, polynomial or not, as long
as the function is differentiable in a desired interval.

3. In order to explain Newton’s
method, imagine that x0 is already
very close to a 0 of f(x). We know
that if we only look at points very
close xo then f(x) looks like its
tangent line. If x0 was already close
to the place where f(x) was 0, and
near x0 we know that f(x) looks like
tangent line, then we hope the 0 of
the tangent line at x0 is a better
approximation then x0 itself.

4. For the value of x where f(x)=0, we choose to call this value of x1
Now, we call x2

5. Example:

6. THANK YOU
Presented by: 49_Aditi Pawaskar