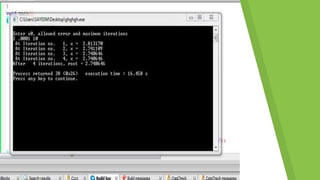
The Newton-Raphson method is an iterative method for finding successively better approximations to the roots (or zeroes) of a real-valued function. It starts with an initial guess x0 and the function's derivative f', and calculates a better approximation x1. The document includes code implementing the Newton-Raphson method to find the root of a cubic function f(x)=x^3 - 2x - 5. It takes inputs of the initial guess x0, allowed error, and maximum iterations and outputs the root if convergence is achieved or indicates non-convergence otherwise. The method has applications in finding extrema of functions, inverting numbers, and solving transcendental equations.

1. Newton–Raphson
Method
MD. ABU BAKAR SIDDIQUE
DEPT. OF INDUSTRIAL & PRODUCTION ENGINEERING
3RD YAER, 6TH SEMESTER
ROLL: 125029
RUET, BANGLADESH.
FACEBOOK: http://bit.ly/2azV80u

2. 1.
Introduction
Let’s start with
the first set of
slides

3. Introduction
In numerical analysis, Newton's method (also known as the Newton–
Raphson method), named after Isaac Newton and Joseph Raphson,
is a method for finding successively better approximations to the
roots (or zeroes) of a real-valued function.
The method starts with a function f defined over the real numbers x,
the function's derivative f', and an initial guess x0 for a root of the
function f. If the function satisfies the assumptions made in the
derivation of the formula and the initial guess is close, then a better
approximation x1 is

4. 2.
Program
Let’s start with
the first set of
slides

5. #include<stdio.h>
#include<math.h>
float f(float x)
{
return x*x*x – 2*x - 5;
}
float df (float x)
{
return 3*x*x - 2;
}
void main()
{
int itr, maxmitr;
float h, x0, x1, allerr;
printf("nEnter x0, allowed error and maximum iterationsn");
scanf("%f %f %d", &x0, &allerr, &maxmitr);
for (itr=1; itr<=maxmitr; itr++)

6. {
h=f(x0)/df(x0);
x1=x0-h;
printf(" At Iteration no. %3d, x = %9.6fn", itr, x1);
if (fabs(h) < allerr)
{
printf("After %3d iterations, root = %8.6fn", itr, x1);
return 0;
}
x0=x1;
}
printf(" The required solution does not converge or iterations are
insufficientn");
return 1;
}

7. 3.
I/O of The Program

9. 4.
Applications
Let’s start with
the first set of
slides

10.  Newton's method can be used to find a
minimum or maximum of a function.
 Finding the reciprocal of a amounts to finding
the root of the function.
 Solving transcendental equations.
Applications