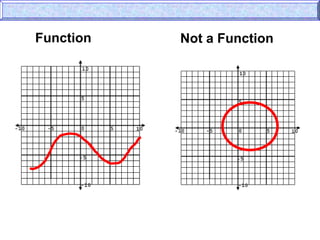
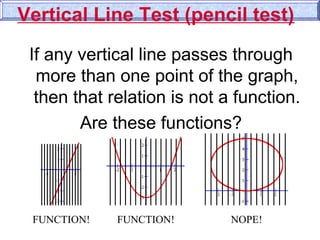
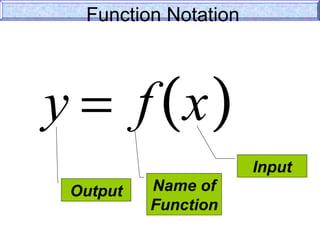
The document provides information about relations and functions: - It defines key terms like relation, domain, range, ordered pair, and function. - It explains how to represent relations using ordered pairs, tables, graphs, and mappings. - It discusses how to determine if a relation is a function using the vertical line test or by checking if each domain value is mapped to only one range value. - It distinguishes between independent and dependent variables in functional notation.

2.  Analyze and graph relations.
 Find functional values.
1) ordered pair
2) Cartesian Coordinate
3) plane
4) quadrant
5) relation
6) domain
7) range
8) function
9) mapping
10) one-to-one function
11) vertical line test
12) independent variable
13) dependent variable
14) functional notation
Relations and FunctionsRelations and Functions

3. Animal
Average
Lifetime
(years)
Maximum
Lifetime
(years)
Cat 12 28
Cow 15 30
Deer 8 20
Dog 12 20
Horse 20 50
This table shows the average lifetime
and maximum lifetime for some animals.
The data can also be represented as
ordered pairs.
The ordered pairs for the data are:
(12, 28), (15, 30), (8, 20),
(12, 20), (20, 50)and
The first number in each ordered pair
is the average lifetime, and the second
number is the maximum lifetime.
(20, 50)
average
lifetime
maximum
lifetime
Relations and FunctionsRelations and Functions

4. Animal Lifetimes
y
x
3010 20 30
60
20
40
60
5 25
10
50
15
30
0
0
Average Lifetime
MaximumLifetime
(12, 28), (15, 30), (8, 20),
(12, 20), (20, 50)and
You can graph the ordered pairs below
on a coordinate system with two axes.
Remember, each point in the coordinate
plane can be named by exactly one
ordered pair and that every ordered pair
names exactly one point in the coordinate
plane.
The graph of this data (animal lifetimes)
lies in only one part of the Cartesian
coordinate plane – the part with all
positive numbers.
Relations and FunctionsRelations and Functions

5. The Cartesian coordinate system is composed of the x-axis (horizontal),
0 5-5
0
5
-5
Origin
(0, 0)
and the y-axis (vertical), which meet at the origin (0, 0) and divide the plane into
four quadrants.
You can tell which quadrant a point is in by looking at the sign of each coordinate of
the point.
Quadrant I
( +, + )
Quadrant II
( --, + )
Quadrant III
( --, -- )
Quadrant IV
( +, -- )
The points on the two axes do not lie in any quadrant.
Relations and FunctionsRelations and Functions

6. In general, any ordered pair in the coordinate
plane can be written in the form (x, y).
A relation is a set of ordered pairs.
The domain of a relation is the set of all first coordinates
(x-coordinates) from the ordered pairs.
The range of a relation is the set of all second coordinates
(y-coordinates) from the ordered pairs.
The graph of a relation is the set of points in the coordinate
plane corresponding to the ordered pairs in the relation.
Relations and FunctionsRelations and Functions
What is a RELATION?

7. Given the relation:
{(2, -6), (1, 4), (2, 4), (0,0), (1, -6), (3, 0)}
State the domain:
D: {0,1, 2, 3}
State the range:
R: {-6, 0, 4}
Relations and FunctionsRelations and Functions
Note: { } are the symbol for "set".
When writing the domain and range,
do not repeat values.

8. {(2, –3), (4, 6), (3, –1), (6, 6), (2, 3)}
domain: {2, 3, 4, 6}
range: {–3, –1, 3, 6}
State the domain and range of the following
relation.
Relations and FunctionsRelations and Functions

9. y
x
(-4,3) (2,3)
(-1,-2)
(0,-4)
(3,-3)
State the domain and range of the relation shown
in the graph.
The relation is:
{ (-4, 3), (-1, 2), (0, -4),
(2, 3), (3, -3) }
The domain is:
{ -4, -1, 0, 2, 3 }
The range is:
{ -4, -3, -2, 3 }
Relations and FunctionsRelations and Functions

10. ACTIVITY TIME!  (20 points)
Form five (5 groups).
Assign group leaders per group.
Let them answer pages 142 – 143. Assign
problem to each group to answer.
Outputs will be written in a Manila Paper.
Assign members who will present the output.
Presentation of outputs will be done AFTER 15
minutes.
The last group to post their output will be the
first to present.
Relations and FunctionsRelations and Functions

11. • Relations can be written in several
ways: ordered pairs, table, graph, or
mapping.
• We have already seen relations
represented as ordered pairs.
Relations and FunctionsRelations and Functions

12. Table
{(3, 4), (7, 2),
(0, -1), (-2, 2),
(-5, 0), (3, 3)}
x y
3 4
7 2
0 -1
-2 2
-5 0
3 3
Relations and FunctionsRelations and Functions

13. Mapping
• Create two ovals with the domain on
the left and the range on the right.
• Elements are not repeated.
• Connect elements of the domain with
the corresponding elements in the
range by drawing an arrow.
Relations and FunctionsRelations and Functions

14. Mapping
{(2, -6), (1, 4), (2, 4), (0, 0), (1, -6), (3, 0)}
2
1
0
3
-6
4
0
Relations and FunctionsRelations and Functions

15. In summary:
Relations and FunctionsRelations and Functions

16. Relations and FunctionsRelations and Functions
FUNCTIONS
Objective: To recognize whether a
relation is a function or not.

17. What is a FUNCTION?
Relations and FunctionsRelations and Functions

18. A function is a special type of relation in which each element of the domain is paired
with ___________ element in the range.exactly one
A mapping shows how each member of the domain is paired with each member in
the range.
Functions
( ) ( ) ( ){ }4,2,2,0,1,3−
Domain Range
-3
0
2
1
2
4
function
Relations and FunctionsRelations and Functions
ONE-TO-ONE
CORRESPONDENCE
Furthermore, a set of ordered pairs is a function if no two ordered pairs
have equal abscissas.

19. A function is a special type of relation in which each element of the domain is paired
with ___________ element in the range.exactly one
A mapping shows how each member of the domain is paired with each member in
the range.
Functions
( ) ( ) ( ){ }5,4,3,1,5,1−
Domain Range
-1
1
4
5
3
function,
not one-to-one
Relations and FunctionsRelations and Functions
MANY-TO-ONE
CORRESPONDENCE
Furthermore, a set of ordered pairs is a function if no two ordered pairs
have equal abscissas.

20. A function is a special type of relation in which each element of the domain is paired
with ___________ element in the range.exactly one
A mapping shows how each member of the domain is paired with each member in
the range.
Functions
( ) ( ) ( ) ( ){ }6,3,1,1,0,3,6,5 −−
Domain Range
5
-3
1
6
0
1
not a function
Relations and FunctionsRelations and Functions
ONE-TO-MANY
CORRESPONDENCE
Furthermore, a set of ordered pairs is a function if no two ordered pairs
have equal abscissas.

21. y
x
(-4,3) (2,3)
(-1,-2)
(0,-4)
(3,-3)
State the domain and range of the relation shown
in the graph. Is the relation a function?
The relation is:
{ (-4, 3), (-1, 2), (0, -4), (2, 3), (3, -3) }
The domain is:
{ -4, -1, 0, 2, 3 }
The range is:
{ -4, -3, -2, 3 }
Each member of the domain is paired with
Exactly one member of the range, so
this relation is a function.
Relations and FunctionsRelations and Functions

22. Function Not a Function
(4,12)
(5,15)
(6,18)
(7,21)
(8,24)
(4,12)
(4,15)
(5,18)
(5,21)
(6,24)

23. Function Not a Function
10
3
4
7
5
2
3
4
8
10
3
5
7
2
2
3
4
7
5

24. Function Not a Function
-3
-2
-1
0
1
-6
-1
-0
3
15
-3
-2
-1
0
1
-6
-1
-0
3
15

25. Function Not a Function
X Y
1 2
2 4
3 6
4 8
5 10
6 12
X Y
1 2
2 4
1 5
3 8
4 4
5 10

26. Function
Not a Function
X -3 0 3 8 -10
Y 6 8 20 4 8
X -2 0 -2 7 -8
Y 6 8 20 4 8

27. ANSWER EXERCISE 7,
IDENTIFY WHICH ONES
ARE FUNCTIONS.
1. FUNCTION
2. NOT FUNCTION
3. FUNCTION
4. FUNCTION
5. FUNCTION
Relations and FunctionsRelations and Functions
Let’s check!
NOW YOU TRY!  (2 minutes)

28. You can use the vertical line test to determine whether a relation is a function.
Vertical Line Test
y
x
y
x
If no vertical line intersects a
graph in more than one point,
the graph represents a function.
If some vertical line intercepts a
graph in two or more points, the
graph does not represent a function.
Relations and FunctionsRelations and Functions

29. Year
Population
(millions)
1950 3.9
1960 4.7
1970 5.2
1980 5.5
1990 5.5
2000 6.1
The table shows the population of Indiana
over the last several decades.
We can graph this data to determine
if it represents a function.
7‘60
0
1
3
5
7
2
6
‘50
8
4
‘80‘70 ‘00
0
‘90
Population
(millions)
Year
Population of Indiana
Use the vertical
line test.
Notice that no vertical line can be drawn that
contains more than one of the data points.
Therefore, this relation is a function!Therefore, this relation is a function!
Relations and FunctionsRelations and Functions

30. Function Not a Function

31. Function Not a Function

32. Function Not a Function

33. SHORT QUIZ #3: (1/4)
Identify if the given
relation is function or
not.

34. -2
-1
-4
-2
0
1
0
2
2 4
-2
-1
0
10
1
2
2
3.
0
1
2
-2
-1
0
1
2
2.1.

35. x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
3.

36. x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
3. 4.

37. x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
4. 5. 6.

38. x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
4. 5. 6. 7.

39. x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
4. 5. 6. 7.
8. 9.
10. 11.

40. input output
0
1
5
2
3
yx
-3
-3
-3
-3
-1
0
1
2
x
y
input output
-2
-1
0
3
4
5
6
12.
13.
14.
15.

41. Let’s Check!
Answers

42. -2
-1
-4
-2
0
1
0
2
2 4
Function
-2
-1
0
10
1
2
2
Function Not a Function
3.
0
1
2
-2
-1
0
1
2
2.1.

43. x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
Function Function Not a
Function
Function
Not a
Function
Function Not a
Function
Not a
Function
4. 5. 6. 7.
8. 9.
10. 11.

44. input output
0
1
5
2
3
yx
-3
-3
-3
-3
-1
0
1
2
x
y
Function
Not a
Function
Not a
Function
input output
-2
-1
0
3
4
5
6
Not a
Function
12.
13.
14.
15.

45. Determine whether each
relation is a function.
1. {(2, 3), (3, 0), (5, 2), (4, 3)}
YES, every domain is different!
f(x)
2 3
f(x)
3 0
f(x)
5 2
f(x)
4 3

46. Determine whether the relation
is a function.
2. {(4, 1), (5, 2), (5, 3), (6, 6), (1, 9)}
f(x)
4 1
f(x)
5 2
f(x)
5 3
f(x)
6 6
f(x)
1 9
NO,
5 is paired with 2 numbers!

47. Is this relation a function?
{(1,3), (2,3), (3,3)}
1. Yes
2. No
Answer Now

48. Vertical Line Test (pencil test)
If any vertical line passes through
more than one point of the graph,
then that relation is not a function.
Are these functions?
FUNCTION! FUNCTION! NOPE!

49. Vertical Line Test
NO!
FUNCTION!
FUNCTION!
NO!

50. Is this a graph of a function?
1. Yes
2. No
Answer Now

51. When an equation represents a function, the variable (usually x) whose values make
up the domain is called the independent variable.
Relations and FunctionsRelations and Functions

52. When an equation represents a function, the variable
(usually x) whose values make up the
domain is called the independent variable.
The other variable (usually y) whose values make
up the range is called the dependent variable
because its values depend on x.
Relations and FunctionsRelations and Functions

53. Function Notation
• When we know that a relation is a
function, the “y” in the equation can
be replaced with f(x).
• f(x) is simply a notation to designate a
function. It is pronounced ‘f’ of ‘x’.
• The ‘f’ names the function, the ‘x’ tells
the variable that is being used.
NOTE: Letters other than f can be used to represent
a function.
EXAMPLE: g(x) = 2x + 1

54. Function Notation
Output
Input
Name of
Function
y = f x( )

55. Given f(x) = 3x - 2, find:
1) f(3)
2) f(-2)
3(3)-23 7
3(-2)-2-2 -8
= 7
= -8

56. Given h(z) = z2
- 4z + 9, find h(-
3)
(-3)2
-4(-3)+9-3 30
9 + 12 + 9
h(-3) = 30

57. Given: f(x) = x2
+ 2 and g(x) = 0.5x2
– 5x + 3.5
Find each value.
Relations and FunctionsRelations and Functions

58. Given: f(x) = x2
+ 2 and g(x) = 0.5x2
– 5x + 3.5
f(-3)
Find each value.
Relations and FunctionsRelations and Functions

59. Given: f(x) = x2
+ 2 and g(x) = 0.5x2
– 5x + 3.5
f(-3)
f(x) = x2
+ 2
Find each value.
Relations and FunctionsRelations and Functions

60. Given: f(x) = x2
+ 2 and g(x) = 0.5x2
– 5x + 3.5
f(-3)
f(x) = x2
+ 2
Find each value.
f(-3) = (-3)2
+ 2
Relations and FunctionsRelations and Functions

61. Given: f(x) = x2
+ 2 and g(x) = 0.5x2
– 5x + 3.5
f(-3)
f(x) = x2
+ 2
Find each value.
f(-3) = (-3)2
+ 2
f(-3) = 9 + 2
Relations and FunctionsRelations and Functions

62. Given: f(x) = x2
+ 2 and g(x) = 0.5x2
– 5x + 3.5
f(-3)
f(x) = x2
+ 2
Find each value.
f(-3) = (-3)2
+ 2
f(-3) = 9 + 2
f(-3) = 11
Relations and FunctionsRelations and Functions

63. Given: f(x) = x2
+ 2 and g(x) = 0.5x2
– 5x + 3.5
f(-3)
f(x) = x2
+ 2
Find each value.
f(-3) = (-3)2
+ 2
f(-3) = 9 + 2
f(-3) = 11
g(2.8)
Relations and FunctionsRelations and Functions

64. Given: f(x) = x2
+ 2 and g(x) = 0.5x2
– 5x + 3.5
f(-3)
f(x) = x2
+ 2
Find each value.
f(-3) = (-3)2
+ 2
f(-3) = 9 + 2
f(-3) = 11
g(2.8)
g(x) = 0.5x2
– 5x + 3.5
Relations and FunctionsRelations and Functions

65. Given: f(x) = x2
+ 2 and g(x) = 0.5x2
– 5x + 3.5
f(-3)
f(x) = x2
+ 2
Find each value.
f(-3) = (-3)2
+ 2
f(-3) = 9 + 2
f(-3) = 11
g(2.8)
g(x) = 0.5x2
– 5x + 3.5
g(2.8) = 0.5(2.8)2
– 5(2.8) + 3.5
Relations and FunctionsRelations and Functions

66. Given: f(x) = x2
+ 2 and g(x) = 0.5x2
– 5x + 3.5
f(-3)
f(x) = x2
+ 2
Find each value.
f(-3) = (-3)2
+ 2
f(-3) = 9 + 2
f(-3) = 11
g(2.8)
g(x) = 0.5x2
– 5x + 3.5
g(2.8) = 0.5(2.8)2
– 5(2.8) + 3.5
g(2.8) = 3.92 – 14 + 3.5
Relations and FunctionsRelations and Functions

67. Given: f(x) = x2
+ 2 and g(x) = 0.5x2
– 5x + 3.5
f(-3)
f(x) = x2
+ 2
Find each value.
f(-3) = (-3)2
+ 2
f(-3) = 9 + 2
f(-3) = 11
g(2.8)
g(x) = 0.5x2
– 5x + 3.5
g(2.8) = 0.5(2.8)2
– 5(2.8) + 3.5
g(2.8) = 3.92 – 14 + 3.5
g(2.8) = – 6.58
Relations and FunctionsRelations and Functions

68. Given g(x) = x2
– 2, find g(4)
Answer Now
1. 2
2. 6
3. 14
4. 18

69. Given f(x) = 2x + 1, find f(-8)
Answer Now
1. -40
2. -15
3. -8
4. 4

70. Value of a Function
If g(s) = 2s + 3, find g(-2).
g(-2) = 2(-2) + 3
=-4 + 3
= -1
g(-2) = -1

71. Value of a Function
If h(x) = x2
- x + 7, find h(2c).
h(2c) = (2c)2
– (2c) + 7
= 4c2
- 2c + 7

72. Value of a Function
If f(k) = k2
- 3, find f(a - 1)
f(a - 1)=(a - 1)2
- 3
(Remember FOIL?!)
=(a-1)(a-1) - 3
= a2
- a - a + 1 - 3
= a2
- 2a - 2

73. 12relationGraph the += xy
x y
1) Make a table of values.
-1
0
1
2
-1
1
3
5
2) Graph the ordered pairs.
0
y
0 x
5-4 -2 1 3
-3-3
-1
2
4
6
-5 -1 4
-2
3
-5 2
1
-3
5
7
3) Find the domain and range.
Domain is all real numbers.
Range is all real numbers.
4) Determine whether the relation is a function.
The graph passes the vertical line test.
For every x value there is exactly one y value,
so the equation y = 2x + 1 represents a function.
For every x value there is exactly one y value,
so the equation y = 2x + 1 represents a function.
Relations and FunctionsRelations and Functions

74. 2relationGraph the 2
−= yx
x y
1) Make a table of values.
2
-1
-2
-2
-1
0
2) Graph the ordered pairs.
0
y
0 x
5-4 -2 1 3
-3-3
-1
2
4
6
-5 -1 4
-2
3
-5 2
1
-3
5
7
3) Find the domain and range.
Domain is all real numbers,
greater than or equal to -2.
Range is all real numbers.
4) Determine whether the relation is a function.
The graph does not pass the vertical line test.
For every x value (except x = -2),
there are TWO y values,
so the equation x = y2
– 2
DOES NOT represent a function.
For every x value (except x = -2),
there are TWO y values,
so the equation x = y2
– 2
DOES NOT represent a function.
-1 1
2 2
Relations and FunctionsRelations and Functions

75. Graphs of a Function
Vertical Line Test:
If a vertical line is passed
over the graph and it intersects
the graph in exactly one point,
the graph represents a function.

76. x
y
x
y
Does the graph represent a
function? Name the domain and
range.
Yes
D: all real numbers
R: all real numbers
Yes
D: all real numbers
R: y ≥ -6

77. x
y
x
y
Does the graph represent a
function? Name the domain and
range.
No
D: x ≥ 1/2
R: all real numbers
No
D: all real numbers
R: all real numbers

78. Does the graph represent a
function? Name the domain and
range.
Yes
D: all real numbers
R: y ≥ -6
No
D: x = 2
R: all real numbers
x
y
x
y

79. Relations and FunctionsRelations and Functions